Two charges of magnitudes +4Q and -Q and located at points (a, 0) and (-3a, 0) respectively. What is the electric flux due to these charges through a sphere of radius '2a' with its centre at the orgin ?
To find the electric flux due to the charges +4Q and -Q through a sphere of radius 2a centered at the origin, we can follow these steps:
1. Identify the Charges and Their Positions:
- The charge +4Q is located at the point (a, 0).
- The charge -Q is located at the point (-3a, 0).
2. Determine the Sphere's Radius and Center:
- The sphere has a radius of 2a and is centered at the origin (0, 0).
3. Check Which Charges Are Inside the Sphere:
- The charge +4Q at (a, 0) is inside the sphere since its distance from the origin is a, which is less than 2a.
- The charge -Q at (-3a, 0) is outside the sphere since its distance from the origin is 3a, which is greater than 2a.
4. Apply Gauss's Law:
- According to Gauss's Law, the electric flux (Φ) through a closed surface is given by:
Φ=Qencϵ0
- Where Qenc is the total charge enclosed by the surface and ϵ0 is the permittivity of free space.
5. Calculate the Enclosed Charge:
- The only charge enclosed by the sphere is +4Q.
- Therefore, Qenc=+4Q.
6. Calculate the Electric Flux:
- Substituting the enclosed charge into Gauss's Law:
Φ=4Qϵ0
Final Answer:
The electric flux through the sphere of radius 2a centered at the origin is:
Φ=4Qϵ0
- The charge +4Q is located at the point (a, 0).
- The charge -Q is located at the point (-3a, 0).
- The sphere has a radius of 2a and is centered at the origin (0, 0).
- The charge +4Q at (a, 0) is inside the sphere since its distance from the origin is a, which is less than 2a.
- The charge -Q at (-3a, 0) is outside the sphere since its distance from the origin is 3a, which is greater than 2a.
- According to Gauss's Law, the electric flux (Φ) through a closed surface is given by:
Φ=Qencϵ0
- Where Qenc is the total charge enclosed by the surface and ϵ0 is the permittivity of free space.
- The only charge enclosed by the sphere is +4Q.
- Therefore, Qenc=+4Q.
- Substituting the enclosed charge into Gauss's Law:
Φ=4Qϵ0
The electric flux through the sphere of radius 2a centered at the origin is:
Φ=4Qϵ0
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET-III DELHI BOARD
10 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET -I
29 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET III
7 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
Two charges of magnitude −2Qand+Q are located at points (a,0)and(4a,0) respectively .
What is the electric flux due to charges through a sphere of radius '3a' with its center at the origin.
View SolutionTwo point charges q and –q are at positions (0,0,d) and (0,0, –d) respectively . What is the electric field at (a,0,0 ) ?
View SolutionTwo point charges q and –q are at positions (0,0,d) and (0,0, –d) respectively . What is the electric field at (a,0,0 ) ?
View SolutionTwo fixed charges −2Q and +Q are located at points (−3a,0) and (+3a,0) respectively. Then which of the following statement is correct?
View SolutionTwo point charges −q and +q are located at points (0,0−a) and (0,0,a) respectively. The electric potential at point (0,0,z)is (Z>a)
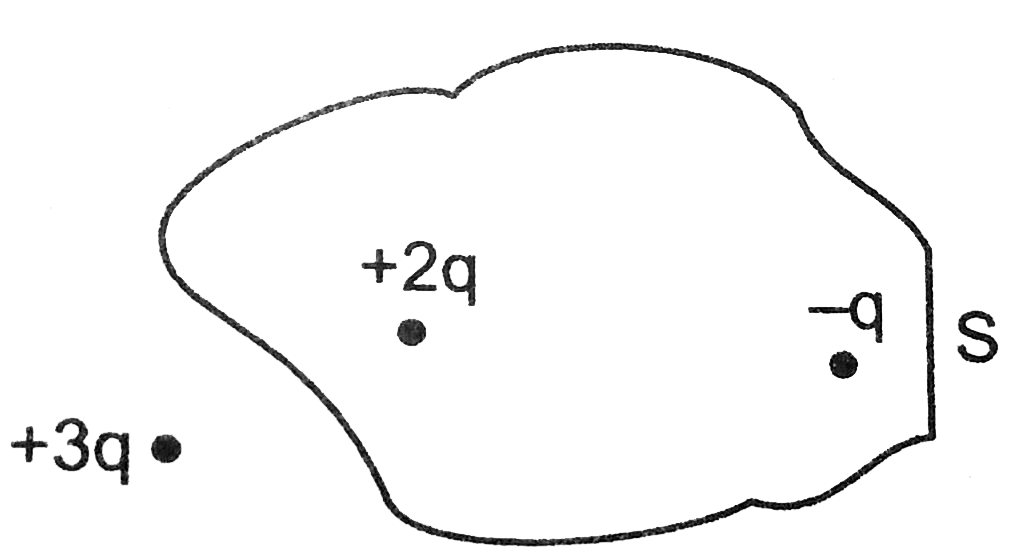
View SolutionFig shows three point charges +2q,−qand+3q, What is the electric flux due to this configuration through the surface S ?
View SolutionTwo point charges of magnitude +qand−q are placed at (−d/2,0,0)and(d/2,0,0) are respectively. Find the equation of the euipotential surface where the potential is zero.
View SolutionA point charge q is placed at origin. Find the flux of electric,produced due to this charge, through a circle of radius R lying in y-z plane. The centre of the circle lies at (x,0).
View SolutionA charge q is placed at the centre of a cube. What is the electric flux passing through the cube?
View SolutionPoint charges +4q,−q and +4q are kept on the x-axis at points x=0,x=a and x=2a respectively, then
View Solution
