Two charges of magnitude −2Qand+Q are located at points (a,0)and(4a,0) respectively .
What is the electric flux due to charges through a sphere of radius '3a' with its center at the origin.
To solve the problem, we need to find the electric flux through a sphere of radius '3a' centered at the origin due to two charges: −2Q located at (a,0) and +Q located at (4a,0).
1. Identify the Charges and Their Positions:
- We have two charges:
- Charge 1: −2Q at position (a,0)
- Charge 2: +Q at position (4a,0)
2. Determine the Gaussian Surface:
- The Gaussian surface is a sphere of radius 3a centered at the origin (0,0).
- This sphere will extend from −3a to 3a along the x-axis.
3. Check Which Charges Are Inside the Gaussian Surface:
- The charge −2Q at (a,0) is inside the sphere since a<3a.
- The charge +Q at (4a,0) is outside the sphere since 4a>3a.
4. Apply Gauss's Law:
- According to Gauss's Law, the electric flux Φ through a closed surface is given by:
\(
Φ = \frac{Q_{\text{enc}}}{\epsilon_0}
\)
- Where Qenc is the total charge enclosed by the Gaussian surface.
5. Calculate the Enclosed Charge:
- The only charge enclosed by the sphere is −2Q.
- Therefore, Qenc=−2Q.
6. Calculate the Electric Flux:
- Substitute Qenc into Gauss's Law:
\(
Φ = \frac{-2Q}{\epsilon_0}
\)
7. Interpret the Result:
- The negative sign indicates that the electric field lines are entering the surface, meaning the net electric flux is directed inward.
Final Answer:
The electric flux through the sphere of radius 3a is:
\(
Φ = \frac{-2Q}{\epsilon_0}
\)
- We have two charges:
- Charge 1: −2Q at position (a,0)
- Charge 2: +Q at position (4a,0)
- The Gaussian surface is a sphere of radius 3a centered at the origin (0,0).
- This sphere will extend from −3a to 3a along the x-axis.
- The charge −2Q at (a,0) is inside the sphere since a<3a.
- The charge +Q at (4a,0) is outside the sphere since 4a>3a.
- According to Gauss's Law, the electric flux Φ through a closed surface is given by:
\(
Φ = \frac{Q_{\text{enc}}}{\epsilon_0}
\)
- Where Qenc is the total charge enclosed by the Gaussian surface.
- The only charge enclosed by the sphere is −2Q.
- Therefore, Qenc=−2Q.
- Substitute Qenc into Gauss's Law:
\(
Φ = \frac{-2Q}{\epsilon_0}
\)
- The negative sign indicates that the electric field lines are entering the surface, meaning the net electric flux is directed inward.
The electric flux through the sphere of radius 3a is:
\(
Φ = \frac{-2Q}{\epsilon_0}
\)
Topper's Solved these Questions
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [Set- II]4videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [Set-III]3videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET-III, DELHI BOARD4videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
Two charges of magnitudes +4Q and -Q and located at points (a, 0) and (-3a, 0) respectively. What is the electric flux due to these charges through a sphere of radius '2a' with its centre at the orgin ?
View SolutionTwo point charges q and –q are at positions (0,0,d) and (0,0, –d) respectively . What is the electric field at (a,0,0 ) ?
View SolutionTwo point charges q and –q are at positions (0,0,d) and (0,0, –d) respectively . What is the electric field at (a,0,0 ) ?
View SolutionTwo fixed charges −2Q and +Q are located at points (−3a,0) and (+3a,0) respectively. Then which of the following statement is correct?
View SolutionTwo point charges −q and +q are located at points (0,0−a) and (0,0,a) respectively. The electric potential at point (0,0,z)is (Z>a)
View SolutionTwo point charges +q and -q are held fixed at (−a,0) and (a,0) respectively of a x-y coordinate system then
View SolutionTwo point charges of magnitude +qand−q are placed at (−d/2,0,0)and(d/2,0,0) are respectively. Find the equation of the euipotential surface where the potential is zero.
View SolutionFig shows three point charges +2q,−qand+3q, What is the electric flux due to this configuration through the surface S ?
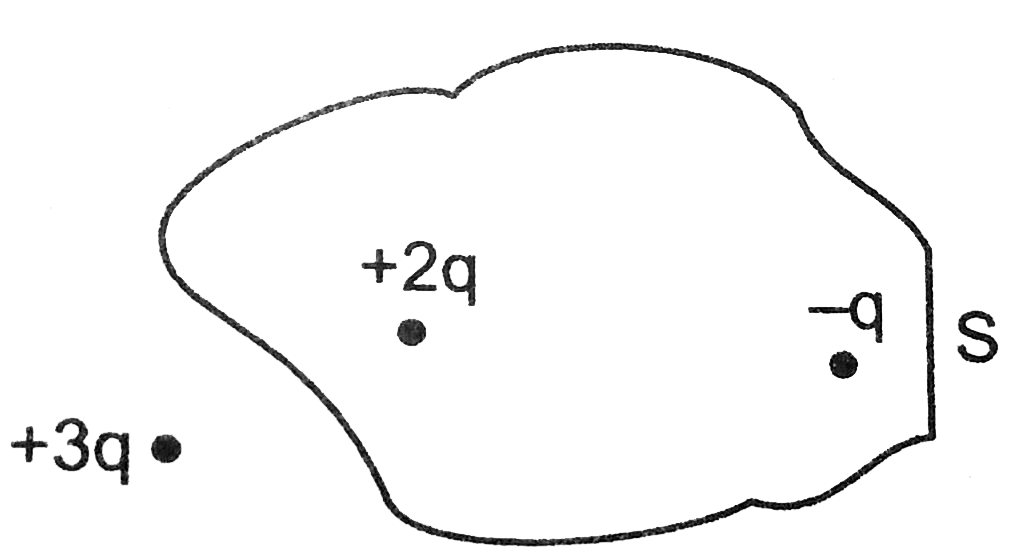 View Solution
View SolutionTwo fixed charges -2Q and Q are located at the point with coordinates (-3a,0) and (+3a,0) respectively in the x- y plane .
Show that all points in the x-y plane where the electric potential due to the two charge is zero , lie on a circle. If its radius is r = xa and the location of its centre is (ya,0) find x and y .View SolutionA point charge Q is placed at the origin . Find the electrostatic energy stored outside the sphere of radius R centred at the origin.
View Solution

