A convex lens is placed in contact with a plane mirror. An axial point object at a distance of 20cm from this combination, has its image coinciding with itself. What is the focal length of the convex lens ?
To solve the problem, we need to analyze the situation where a convex lens is placed in contact with a plane mirror, and an object is placed at a distance of 20 cm from this combination. The image formed coincides with the object itself, indicating that the image distance (v) is equal to the object distance (u) but with a negative sign, since the image is virtual.
1. Understanding the Setup:
- We have a convex lens in contact with a plane mirror.
- An object is placed 20 cm away from the lens-mirror combination.
2. Identify Object and Image Distances:
- Let the object distance (u) be -20 cm (the negative sign indicates that the object is on the same side as the incoming light).
- Since the image coincides with the object, the image distance (v) is also -20 cm.
3. Using the Lens Formula:
The lens formula is given by:
1f=1v−1u
where f is the focal length of the lens.
4. Substituting Values:
- Substitute u=−20 cm and v=−20 cm into the lens formula:
1f=1−20−1−20
1f=−120+120=0
5. Finding Focal Length:
- Since 1f=0, it implies that:
f=∞
This means that the focal length of the convex lens is effectively infinite.
Conclusion:
The focal length of the convex lens in this configuration is infinite.
- We have a convex lens in contact with a plane mirror.
- An object is placed 20 cm away from the lens-mirror combination.
- Let the object distance (u) be -20 cm (the negative sign indicates that the object is on the same side as the incoming light).
- Since the image coincides with the object, the image distance (v) is also -20 cm.
The lens formula is given by:
1f=1v−1u
where f is the focal length of the lens.
- Substitute u=−20 cm and v=−20 cm into the lens formula:
1f=1−20−1−20
1f=−120+120=0
- Since 1f=0, it implies that:
f=∞
This means that the focal length of the convex lens is effectively infinite.
The focal length of the convex lens in this configuration is infinite.
Topper's Solved these Questions
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [SET - II DELHI BOARD]5videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [SET - III, DELHI BOARD]6videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET-II33videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
A thin convex lens of focal length 30cm is placed in front of a plane mirror. An object is placed at a distance x from the lens (not in between lens and mirror ) so that its final image coincides with itself. Then, the value of x is
View SolutionA point object is placed at a distance of 12cm from a convex lens of focal length 10cm. On the other side of the lens, a convex mirror is placed at a distance of 10cm from the lens such that the image formed by the combination coincides with the object itself. The focal length of the convex mirror is
View Solution
Knowledge Check
- Question 1 - Select One
A convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
Areal, at 30 cm in front of the mirrorBreal, at 30 cm behind the mirrorCreal, at 10 cm in front of the mirrorDvirtual, at 10 cm behind the mirror - Question 2 - Select One
A concave lens is placed in contact with a convex lens of focal length 25cm. The combination produces a real image at a distance of 80cm, when an object is at a distance of 40cm. What is the focal length of concave lens ?
A−400cmB−200cmC+400cmD+200cm
A point object O is placed at a distance of 15 cm from a convex lens L of focal length 10 cm as shown in figure below. On the other side of the lens, a convex mirror M is placed such that its distance from the lens is equal to the focal length of the lens. The final image formed by this combination is observed to coincide with the object 0. Find the focal length of the convex mirror.
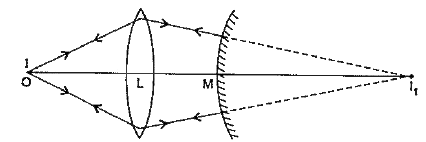 View Solution
View SolutionAn object is placed at a distance of 15cm from a convex lenx of focal length 10cm. On the other side of the lens, a convex mirror is placed at its focus such that the image formed by the combination coincides with the object itself. The focal length of the convex mirror is
View SolutionAn object is placed 30cm away from a convex lens of focal length 10cm and a sharp image is formed on a screen. Now, a convex lens is placed In contact with the convex lens. The screen now has to be moved by 45cm to get a sharp image again. The magnitude of focal length of the convex lends in (in cm)
View SolutionFind the distance of an object from a convex lens if image is
two times magnified. Focal length of the lens is 10cmView SolutionFind the distance of an object from a convex lens if image is
two times magnified. Focal length of the lens is 10cmView SolutionA convex lens of focal length 40 cm is in contact with a concave lens of focal length 25 cm. The power of the combination is
View Solution

