(a) How does one demonstrate, using a suitable diagram, that unpolarised light when passed through a Polaroid gets polarised?
(b) A beam of unpolarised light is incident a glass-air interface. Show using a suitable ray diagram, that light reflected from the interface is totally polarised, when μ=taniB, when μ is the refractive index of glass with respect to air and iB, is the Brewster's angle.
(a) (i) Two independent monochromatic sources of light cannot produce a sustained interference patter. The phase difference between these two sources will continuously vary, and the positions of maxima and minima will change with time.
(ii) y1=acosωt,andy2=acos(ωt+ϕ)
y=y1+y2=a[cosωt+cos(ωt+ϕ)
=2acos(ϕ2)cos(ωt+ϕ2)
The resultant amplitude is A=2acos(ϕ2)
and hence intensity (I)=4a2cos2(ϕ2)=4I0cos2(ϕ2).
The intensity of light is directly proportional to the square of the amplitude of the wave. intensity of light at point P on the screen is given by :
I=4a2cos2(ϕ)2.
(a)
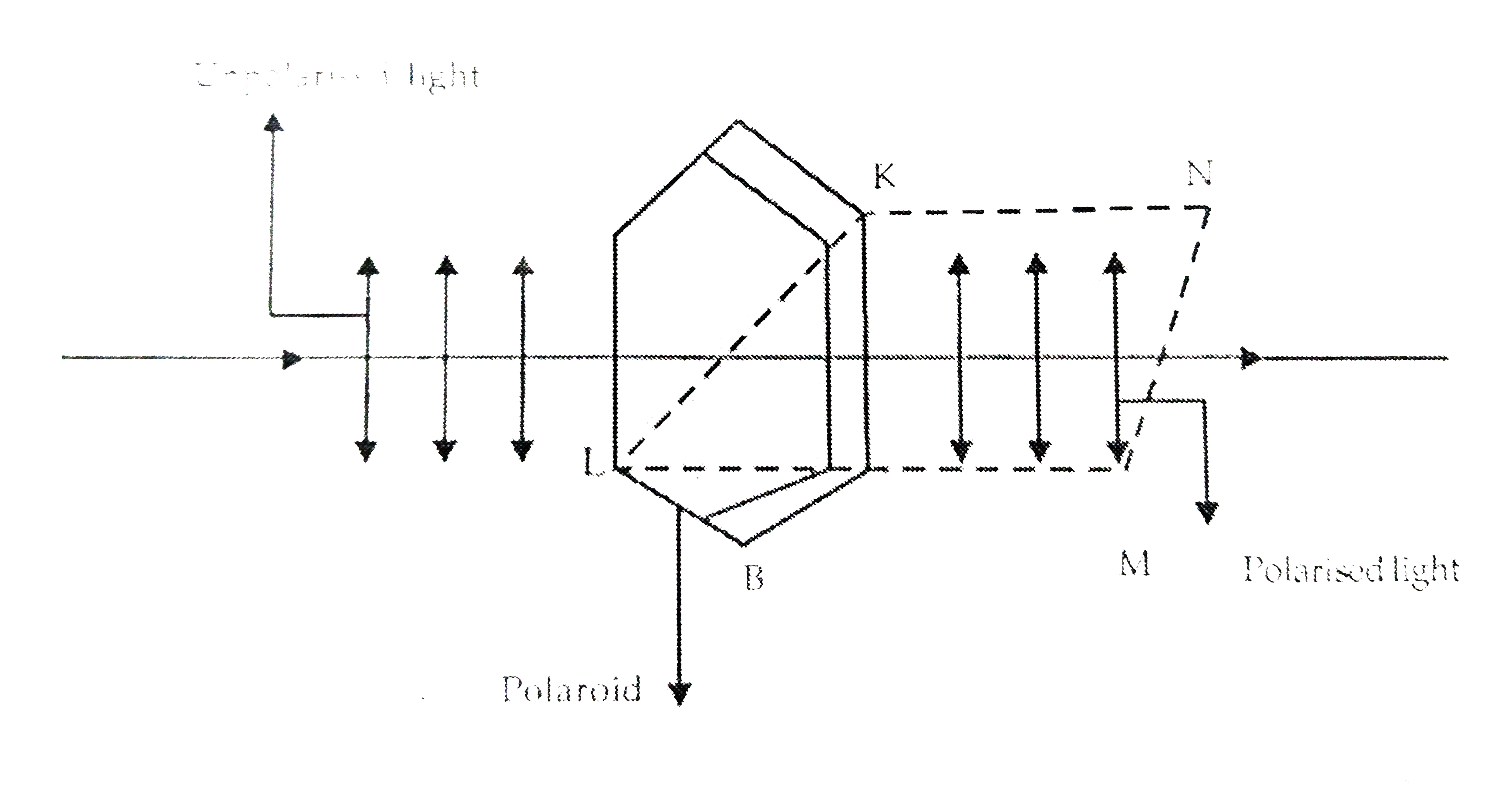
The phenomenon of restricting the vibration of light (electric vector) in a particular direction perpendicular to the direction of the wave propagation is called polarisation of light.
When unpolarised light is passed through a polaroid, only those bibrations of light pass through the crystal, which are parallel to the axis of the crystal (AB). All other vibrations are absorbed and that is why intensity of the emerging light is reduced.
The plane ABCD in which the vibrations of the polarise light are confined is called the plane of vibration.
The plane KLMN that is perpendicular to the plane of vibration is defined as the plane of polarization. When light is incident at Brewster angle, the reflected component OB and the refracted component OC are mutually perpendicualr to each other.
From the figure, we have:
∠BOY+∠YOC=90∘
(90∘−iB)+(90∘−r)=90∘
where, r is angle of refraction
90∘−iB=r
according to the Snell's law :
μ=sini−sinri=iBand
r=90∘−iBμ=siniBsin90∘−iB
siniBcosiBμ=taniB.
Hence, Proved.
Topper's Solved these Questions
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [SET - II DELHI BOARD]5videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [SET - III, DELHI BOARD]6videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET-II33videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
Unpolarized light is incident on a plane surface of glass of refractive index μ at angle i. If the reflected light gets totally polarized, write the relation between the angle i and refractive index μ.
View SolutionWhen unpolarised light beam is incident from air onto glass (n=1.5) at the polarising angle
View SolutionWhen unpolarised light beam is incident from air onto glass (n=1.5) at the polarising angle
View SolutionA : When an unpolarised light is incident on a glass plate at Brewster angle, the reflected ray and refracted ray are matually perpendicular.
R : The refractive index of glass is equal to sine of the angle of polarisation.View Solution(a) What is linearly polarized light ? Describe briefly using a diagram how sunlight is polarised.
(b) Unpolarised light is incident on a polaroid. How would the intensity of transmitted light change when the polaroid is rotated?View SolutionThe angle of incidence at which reflected light is totally polarized for reflection from air to glass (refractive index n),
View SolutionThe angle of incidence at which reflected light is totally polarised for reflection from air to glass (refractive index n) is
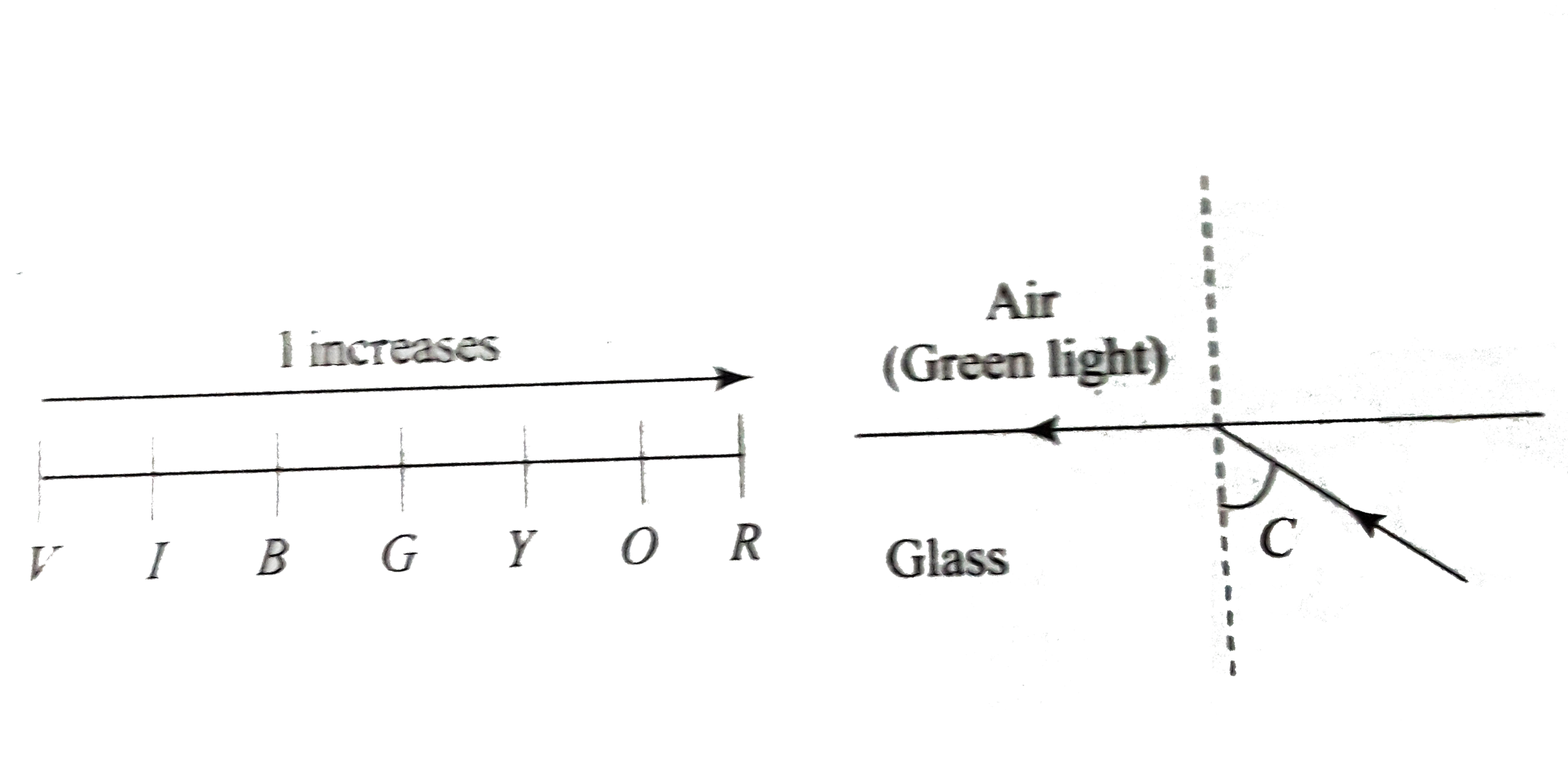
View SolutionA beam of white light is incident on the glass-air interface from glass to air such that green light just suffers total internal reflection. The colors of the light which will come out to air are
 View Solution
View SolutionWhen light wave suffers reflection at the interface from air to glass, the change in phase of the reflected wave is equal to
View SolutionA ray of light is incident on the surface of a glass plate at an angle of incidence equal to Brewster's angle ϕ. If μ represents the refractive index of glass with respect to air, then the angle between reflected and refracted rays is
View Solution

