(a) Explain the processes of nuclear fission and nuclear fusion by using the plot of binding energy per nucleon (BE/A) versus the mass number A.
(b) A radioactive isotope has a hald -life of 10 years. How long will it take for the activity to reduce to 3.125%.
Solution:
(a) Explanation of Nuclear Fission and Nuclear Fusion:
1. Understanding Binding Energy per Nucleon (BE/A):
- The binding energy per nucleon is a measure of the stability of a nucleus. It is plotted against the mass number (A) of the nucleus.
- The graph typically shows that lighter nuclei have lower binding energy per nucleon, while heavier nuclei reach a peak and then start to decrease.
2. Nuclear Fission:
- Nuclear fission is the process where a heavy nucleus splits into two smaller nuclei.
- In the graph, this can be visualized as moving from a heavy nucleus (high mass number) to two smaller nuclei (lower mass numbers).
- As the heavy nucleus splits, the binding energy per nucleon increases, indicating that the resulting smaller nuclei are more stable and energy is released during this process.
3. Nuclear Fusion:
- Nuclear fusion is the process where two light nuclei combine to form a heavier nucleus.
- In the graph, this is represented by moving from two smaller nuclei (lower mass numbers) to a heavier nucleus (higher mass number).
- Similar to fission, the binding energy per nucleon increases, and energy is released as the lighter nuclei combine to form a more stable heavier nucleus.
4. Comparison:
- Both processes release energy, but nuclear fission involves the splitting of heavy nuclei while nuclear fusion involves the combining of light nuclei.
- Additionally, nuclear fusion can be controlled more easily than nuclear fission.
---
(b) Calculation of Time for Activity to Reduce to 3.125%:
1. Given Data:
- Half-life (t_half) = 10 years
- We need to find the time (t) for the activity to reduce to 3.125%.
2. Understanding Activity Reduction:
- 3.125% can be expressed as a fraction:
3.125100=0.03125
- This can also be written as:
NN0=132
- This indicates that the remaining quantity of the substance is 132 of the original amount.
3. Using the Radioactive Decay Formula:
- The formula for radioactive decay is:
NN0=e−λt
- Substituting NN0=132:
132=e−λt
4. Expressing 132 in Terms of Powers of 2:
- We know that:
132=2−5
- Thus, we can rewrite the equation:
2−5=e−λt
5. Taking the Natural Logarithm:
- Taking the natural logarithm of both sides:
−5ln(2)=−λt
- This simplifies to:
λt=5ln(2)
6. Finding the Decay Constant λ:
- The decay constant λ is related to the half-life:
λ=ln(2)thalf=ln(2)10
- Using ln(2)≈0.693:
λ≈0.69310=0.0693 years−1
7. Substituting λ Back into the Equation:
- Now substitute λ back into the equation:
t=5ln(2)λ=5×0.6930.0693
- Calculating this gives:
t≈50 years
Final Answers:
- (a) Nuclear fission and fusion processes are explained using the binding energy vs. mass number graph.
- (b) The time taken for the activity to reduce to 3.125% is approximately 50 years.
---
- The binding energy per nucleon is a measure of the stability of a nucleus. It is plotted against the mass number (A) of the nucleus.
- The graph typically shows that lighter nuclei have lower binding energy per nucleon, while heavier nuclei reach a peak and then start to decrease.
- Nuclear fission is the process where a heavy nucleus splits into two smaller nuclei.
- In the graph, this can be visualized as moving from a heavy nucleus (high mass number) to two smaller nuclei (lower mass numbers).
- As the heavy nucleus splits, the binding energy per nucleon increases, indicating that the resulting smaller nuclei are more stable and energy is released during this process.
- Nuclear fusion is the process where two light nuclei combine to form a heavier nucleus.
- In the graph, this is represented by moving from two smaller nuclei (lower mass numbers) to a heavier nucleus (higher mass number).
- Similar to fission, the binding energy per nucleon increases, and energy is released as the lighter nuclei combine to form a more stable heavier nucleus.
- Both processes release energy, but nuclear fission involves the splitting of heavy nuclei while nuclear fusion involves the combining of light nuclei.
- Additionally, nuclear fusion can be controlled more easily than nuclear fission.
- Half-life (t_half) = 10 years
- We need to find the time (t) for the activity to reduce to 3.125%.
- 3.125% can be expressed as a fraction:
3.125100=0.03125
- This can also be written as:
NN0=132
- This indicates that the remaining quantity of the substance is 132 of the original amount.
- The formula for radioactive decay is:
NN0=e−λt
- Substituting NN0=132:
132=e−λt
- We know that:
132=2−5
- Thus, we can rewrite the equation:
2−5=e−λt
- Taking the natural logarithm of both sides:
−5ln(2)=−λt
- This simplifies to:
λt=5ln(2)
- The decay constant λ is related to the half-life:
λ=ln(2)thalf=ln(2)10
- Using ln(2)≈0.693:
λ≈0.69310=0.0693 years−1
- Now substitute λ back into the equation:
t=5ln(2)λ=5×0.6930.0693
- Calculating this gives:
t≈50 years
- (a) Nuclear fission and fusion processes are explained using the binding energy vs. mass number graph.
- (b) The time taken for the activity to reduce to 3.125% is approximately 50 years.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION - A
7 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION - B
7 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION - E
5 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
Assume that the nuclear binding energy per nucleon (B/A) versus mass number (A) is as shown in the figure. Use
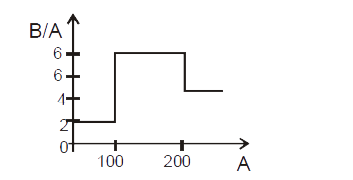
this plot to choose the correct choice(s) given below. Figure
View SolutionAssume that the nuclear binding energy per nucleus(B/A) versus mass number (A) is as shown in the figure Use this plot to choose the correct (s) choice given below

View Solution(a) Name the process, nuclear fission or nuclear fusion, in which the energy released per unit mass is more ?
(b) Name the process, fission or fusion which is possible at ordinary temperature.
View SolutionDefine the activity of a radio nuclide. Write its S.I. unit. Give a plot of the activity of a radioactive species versus time.
How long will a radioactive isotope, whose half life is T years, take for its activity to reduce to 1/8th of its initial value ?
View Solution(i) What characteristic property of nuclear force explains the constancy of binding energy per nucleon (BE/A) in the range of mass number 'A' lying 30<A<170 ?
(ii) Show that the density of nucleus over a wide range of nuclei is constant-independent of mass number A.
View SolutionUsing the curve for the binding energy per nucleon as a function of mass number A, state clearly how the release in energy in the processes of nuclear fission and nuclear fusion can be explained.
View SolutionAssertion: The nuclear energy can be obtained by the nuclear fission of heavier nuclei as well as by fusion of lighter nuclei.
Reason: As the mass number increases, the binding energy per nucleon, first increases and then decreases.
View SolutionAssume that the nuclear binding energy per nucleon (B/A) versus mass number (A) is drawn and is as shown in the figure. Consider a nucleus of A=110. Fission of the nucleus results into 2 fragments Then which of the following sets could be possibly the mass numbers of the resulting nuclei

A) 55 and 55 B) 70 and 40
C) 100 and 10 D) 90 and 20
View SolutionIn the process of nuclear fission of 1g uranium, the mass lost is 0.92mg. The efficiency of power house run by the fission reactor is 10%.To obtain 400 megawatt power from the power house, how much uranium will be required per hour? (c=3×108ms−1).
View SolutionStrontium 90 is one of the harmful nuclides resulting from nuclear fission explosions.
Strontium 90 decays by beta particle emission with a half life of 28 years. How long (in years) would it take for 99.0% of a sample of strontium-90 released in an atmospheric test of an atomic bomb to decay? (log 2 = 0.30)
View Solution
