Combination of Resistance
Step-by-Step Solution for Combination of Resistance
Step 1: Understanding Series Combination of Resistors
In a series combination, resistors are connected end-to-end. The total resistance (R_eq) in a series circuit is the sum of the individual resistances.
Formula:
Req=R1+R2+R3+…+Rn
Step 2: Applying Kirchhoff's Voltage Law
According to Kirchhoff's Voltage Law, the sum of the potential differences (voltage) in a closed loop is equal to zero. For a series circuit, the voltage across the entire circuit (V) is equal to the sum of the voltage drops across each resistor.
Equation:
V−(I⋅R1)−(I⋅R2)−(I⋅R3)=0
Step 3: Rearranging the Equation
From the above equation, we can express the total voltage as:
V=I⋅R1+I⋅R2+I⋅R3
Factoring out the current (I):
V=I⋅(R1+R2+R3)
Step 4: Relating Voltage and Resistance
Since we know that the voltage can also be expressed in terms of the equivalent resistance:
V=I⋅Req
Setting the two expressions for V equal gives us:
I⋅Req=I⋅(R1+R2+R3)
Step 5: Conclusion for Series Combination
Dividing both sides by I (assuming I ≠ 0):
Req=R1+R2+R3
Thus, for n resistors in series:
Req=R1+R2+R3+…+Rn
---
Step 6: Understanding Parallel Combination of Resistors
In a parallel combination, resistors are connected across the same two points. The voltage across each resistor is the same.
Formula:
1Req=1R1+1R2+1R3+…+1Rn
Step 7: Applying Kirchhoff's Current Law
According to Kirchhoff's Current Law, the total current (I) entering a junction is equal to the sum of the currents (I1, I2, I3) leaving the junction.
Equation:
I=I1+I2+I3
Step 8: Expressing Currents in Terms of Voltage and Resistance
For each resistor, the current can be expressed using Ohm's Law:
I1=VR1,I2=VR2,I3=VR3
Substituting these into the current equation gives:
I=VR1+VR2+VR3
Step 9: Factoring Out Voltage
Factoring out the voltage (V):
I=V(1R1+1R2+1R3)
Step 10: Relating Total Current and Equivalent Resistance
Since the total current can also be expressed as:
I=VReq
Setting the two expressions for I equal gives us:
VReq=V(1R1+1R2+1R3)
Step 11: Conclusion for Parallel Combination
Dividing both sides by V (assuming V ≠ 0):
1Req=1R1+1R2+1R3
Thus, for n resistors in parallel:
1Req=1R1+1R2+1R3+…+1Rn
---
Req=R1+R2+R3+…+Rn
V−(I⋅R1)−(I⋅R2)−(I⋅R3)=0
V=I⋅R1+I⋅R2+I⋅R3
V=I⋅(R1+R2+R3)
V=I⋅Req
I⋅Req=I⋅(R1+R2+R3)
Req=R1+R2+R3
Req=R1+R2+R3+…+Rn
1Req=1R1+1R2+1R3+…+1Rn
I=I1+I2+I3
I1=VR1,I2=VR2,I3=VR3
I=VR1+VR2+VR3
I=V(1R1+1R2+1R3)
I=VReq
VReq=V(1R1+1R2+1R3)
1Req=1R1+1R2+1R3
1Req=1R1+1R2+1R3+…+1Rn
Similar Questions
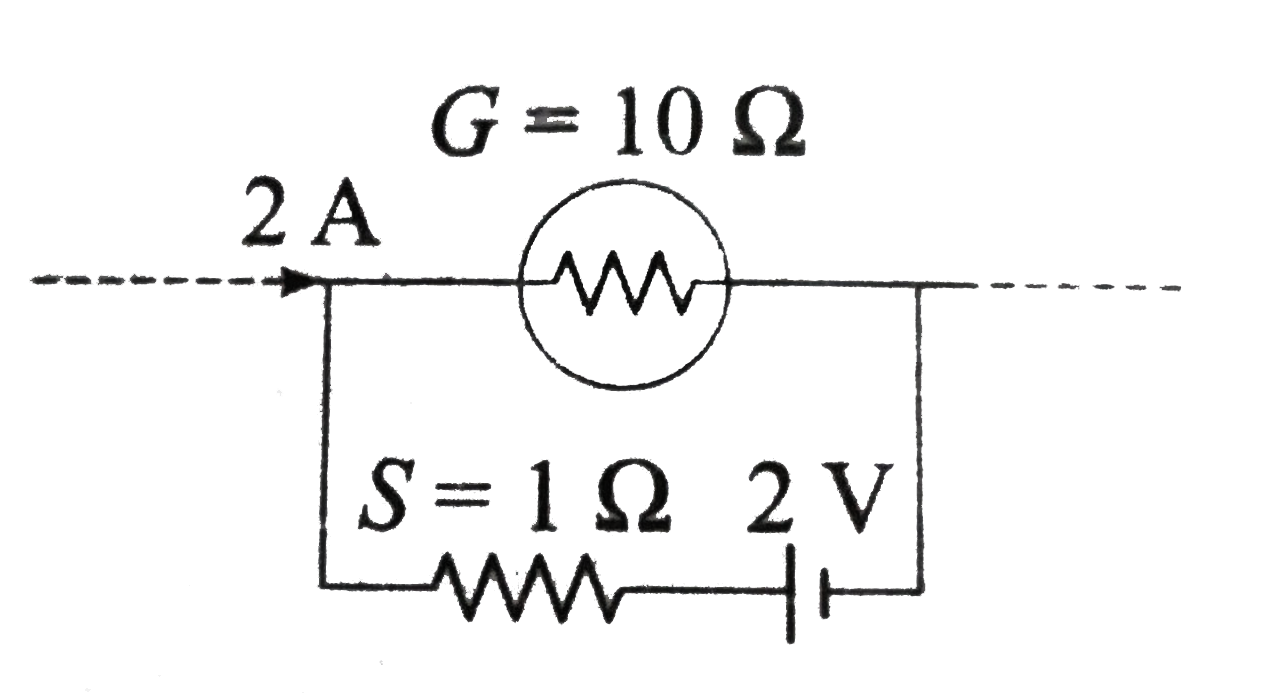
The galvanometer shown in the figure has resistance 10Ω. It is shunted by a series combination of a resistance S=1Ω and an ideal cell of emf 2 V. A current 2 A passes as shown.

View SolutionAn alternating current source of frequency 100Hz is joined to a combination of a resistance, a capacitance and a coil in series. The potential difference across the coil, the resistance and the capacitor is 46,8and40 volt respectively. The electromotive force of alternating current source in volt is
View SolutionThe resistance of a series combination of the resistance is S. when they are joined in parallel equvalent resistance is P. Find the value of (S2P)
View SolutionThe resistance of the series combination of two resistances is S. When they are joined in parallel the total resistance is P. If S= nP then the minimum possible value of n is
View SolutionThe resistance of the series combination of two resistances is S. When they are joined in parallel the total resistance is P. If S= nP then the minimum possible value of n is
View SolutionA carbon and an aluminium wire are connected in series. If the combination has resistance of 30Ω at 30∘C, what is the resistance of each wire at 0∘Cso that resistance of the combination does not change with temperature.(ac=−0.5×10−3/∘C,aA=4×10−3/∘C)
View SolutionConsider the combination of resistor,

The equivalent resistance between a and b is
View SolutionShow how you would connect three resistors, each of 6Ω, so that the combination has a resistance of (a) 9 Ω, (b) 4 Ω.
View SolutionShow how you would connect three resistors, each of resistance 6Ω, so that the combination has a resistance of
(i) 9Ω
(ii) 2Ω.
View SolutionFor the combination of resistors shown in Fig. find the equivalent resistance between the points
A and B

View Solution
