Conservation of Momentum
Step-by-Step Solution:
Step 1: Understand the Definition of Momentum
Momentum (P) is defined as the product of an object's mass (m) and its velocity (v). Mathematically, it is expressed as:
P=m×v
Step 2: State the Principle of Conservation of Momentum
The principle of conservation of momentum states that in a closed system (where no external forces act), the total momentum before a collision is equal to the total momentum after the collision. This can be expressed as:
Pinitial=Pfinal
Step 3: Apply the Concept to Two Objects
Consider two objects, A and B, with momenta P1 and P2 respectively. Before the collision, the total momentum is:
Pinitial=P1+P2
After the collision, let the total momentum be P. According to the conservation of momentum:
Pfinal=P
Step 4: Set Up the Equation
From the principle of conservation of momentum, we can equate the initial and final momentum:
P1+P2=P
This means that the total momentum before the collision is equal to the total momentum after the collision.
Step 5: Conclusion
Thus, the conservation of momentum indicates that the total momentum of two objects before a collision is equal to the momentum of these objects after the collision, confirming that momentum is conserved in an isolated system.
Momentum (P) is defined as the product of an object's mass (m) and its velocity (v). Mathematically, it is expressed as:
P=m×v
The principle of conservation of momentum states that in a closed system (where no external forces act), the total momentum before a collision is equal to the total momentum after the collision. This can be expressed as:
Pinitial=Pfinal
Consider two objects, A and B, with momenta P1 and P2 respectively. Before the collision, the total momentum is:
Pinitial=P1+P2
Pfinal=P
From the principle of conservation of momentum, we can equate the initial and final momentum:
P1+P2=P
Thus, the conservation of momentum indicates that the total momentum of two objects before a collision is equal to the momentum of these objects after the collision, confirming that momentum is conserved in an isolated system.
Similar Questions
A block B is at rest on the rough horizontal surface as shown. Another block A collides with B. Then, which of the following statement is correct?
(i) Impulsive friction acts on block B.
(ii) Conservation of momentum can not be applied on a system (A+B) along x−axis for the situation just before and just after the collision.
(iii) Conservation of momentum can be applied on system (A+B) along x−axis for the situation just before and just after the collision.
(iv) Block A always moves along positive x−axis after collision.

View SolutionYou are standing perfectly still and then you take a step forward. Before the step your momentum was zero, but afterward you have some momentum. Is the principle of conservation of momentum violated in this case?
View Solution
Knowledge Check
Which of the following principles a circus acrobat employs in his performance? a) Conservation of energy b) Conservation of linear momentum c) Conservation of mass d) Conservation of angular momentum
AConservation of energyBConservation of linear momentumCConservation of massDConservation of angular momentumAssertion : A central force is such that the force on the planet is along the vector joining the sun and the planet.
Reason : Conservation of angular momentum is valid for any central force.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are truebut reason is not the correct explanation of assertionCIf assertion is true but reason is falseDIf both assertion and reason are false.
A shell of mass m is moving horizontally with velocity v0 and collides with the wedge of mass M just above points A, as shown in the figure. As a consequences, wedge starts to move towards left and the shell returns with a velocity in xy-plance. The principle of conservation of momentum can be applied for
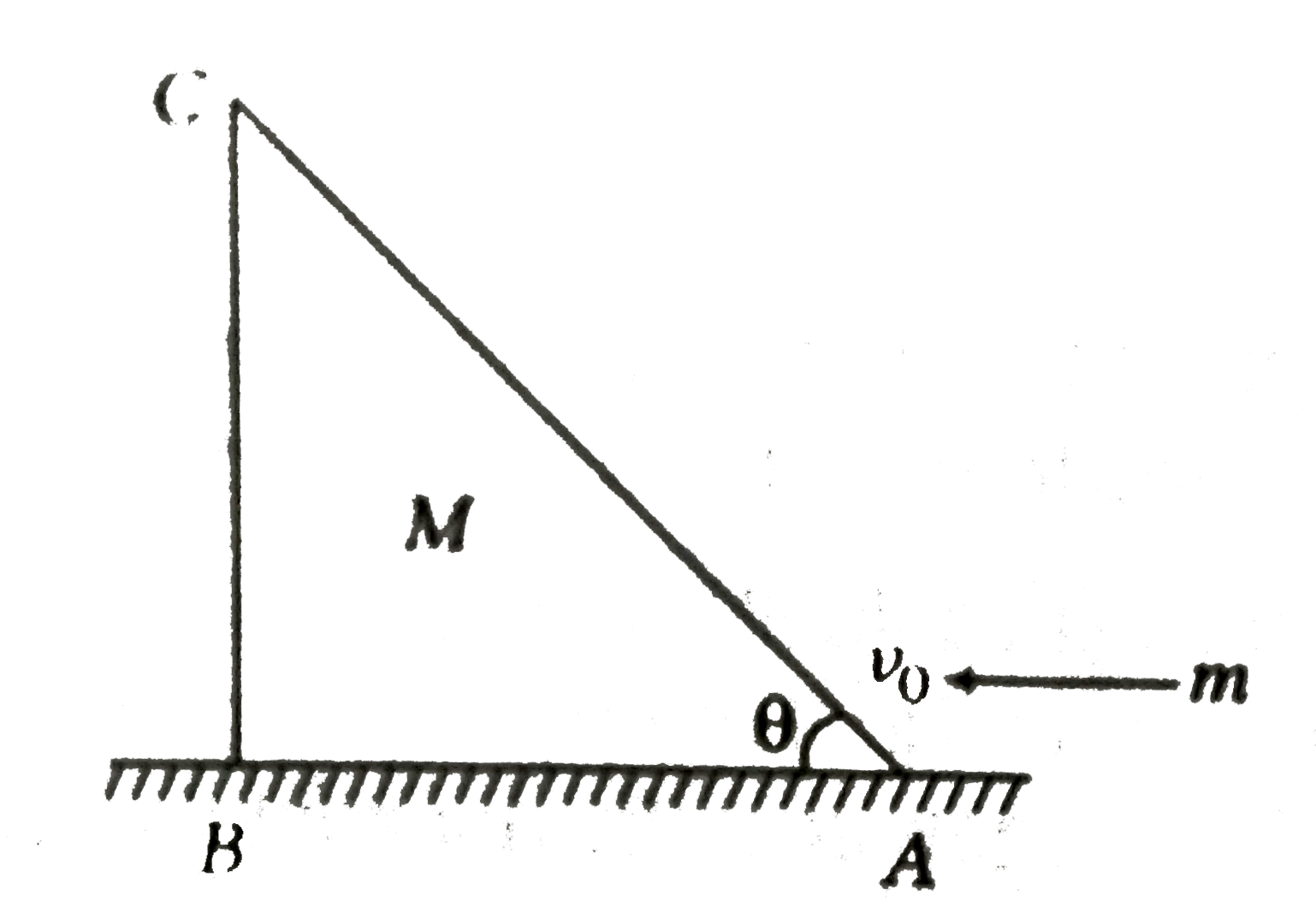
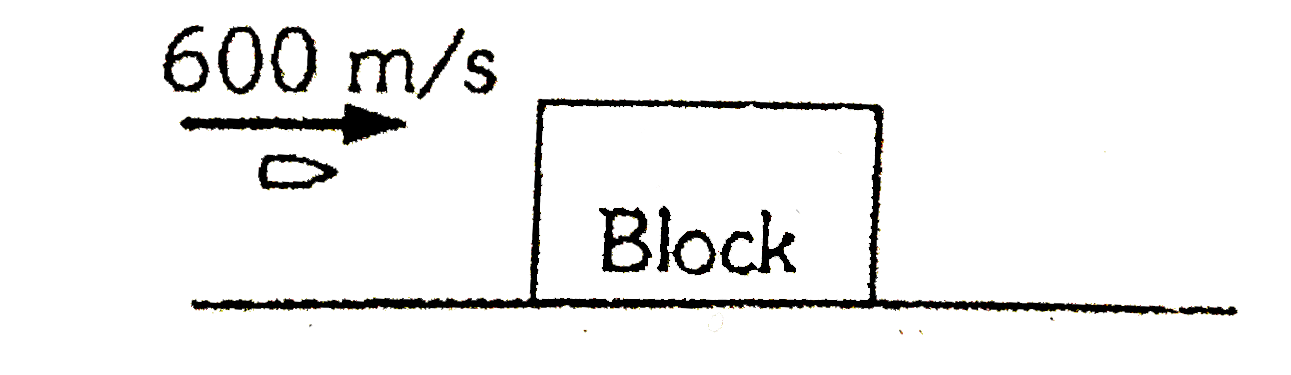
View SolutionA bullet of mass 50g moving with velocity 600m/s hits block of mass 1.0kg placed on a rough horizontal ground and comes out of the block with a velocity of 400m/s. The coefficient of friction between the block and the ground is 0.25. Neglect loss of mass of the block as the bullet pierces through it.
(a) In spite of the fact that friction acts a an external force, can you apply principle of conservation of momentum during interaction of the ullet with the block?
(b) Find velocity of the block immediately after the bullet pierces through it. (c)FInd the distance the block will travel before it stops.
View SolutionConservation is
View SolutionThe electrons in a H- atom kept at rest , jumps from the mth shell to the nth shell (m>n). Suppose instead of emitting electromagnetic wave, the energy released is converted into kinetic energy of the atom. Assuming Bohr's model and conservation of angular momentum are valid. Now , answer the following questions:
What principal is violated of inertia
View SolutionThe electrons in a H- atom kept at rest , jumps from the mth shell to the nth shell (m>n). Suppose instead of emitting electromagnetic wave, the energy released is converted into kinetic energy of the atom. Assuming Bohr's model and conservation of angular momentum are valid. Now , answer the following questions:
Calculate the angular velocity of the atom about the nucleus if l is the momentum of inertia
View SolutionAre conservation of mass and conservation of mechanical energy fundamental laws of nature?
View Solution
