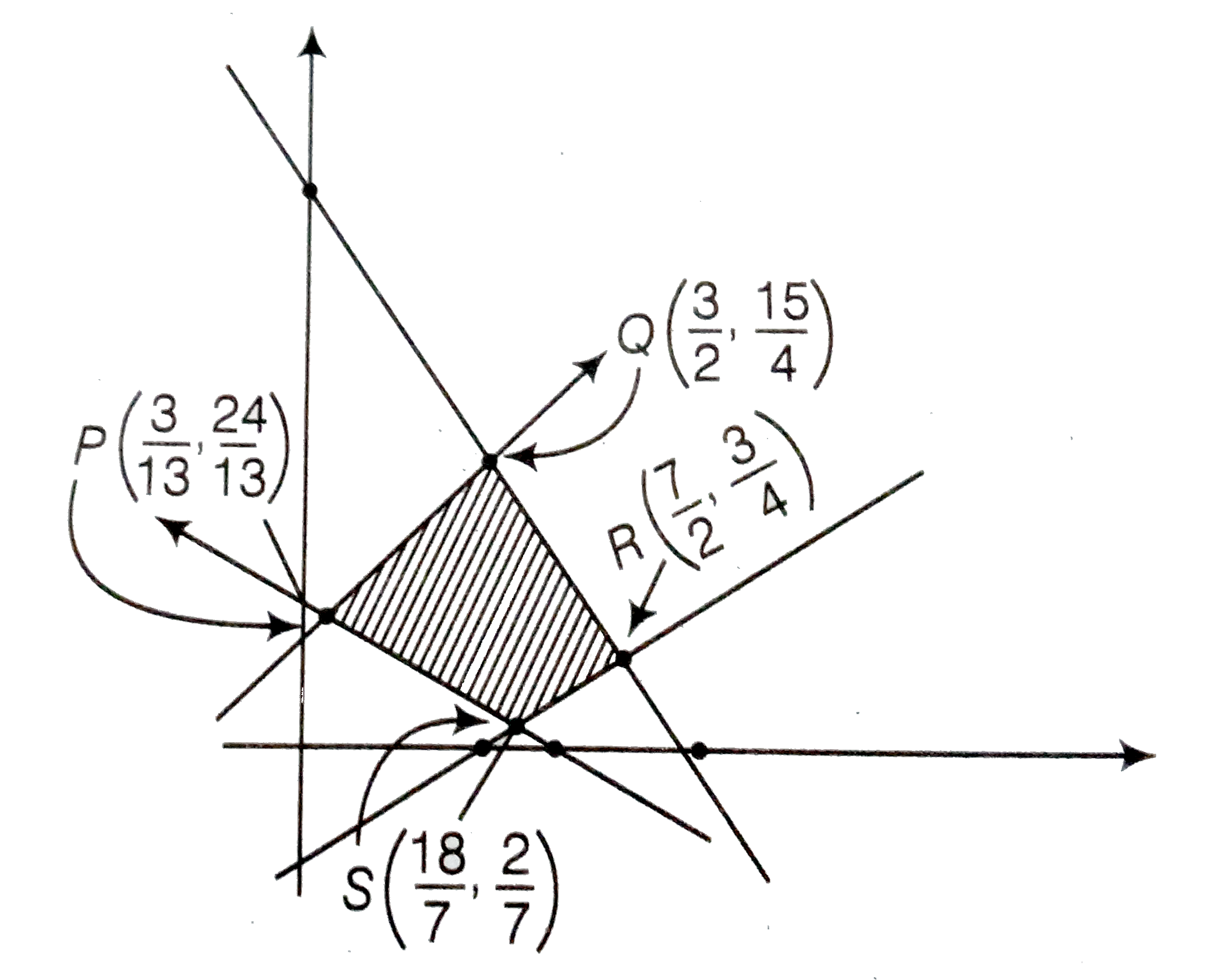
In the following the feasible region (shaded) for a LPP is shown Determine the maximum and minimum value of Z=x+2y
The correct Answer is:N/a
From the shaded bounded region. It is clear the coordinates of corner points are
(313,2413),(187,27),(72,34)and(32,154)
Also we have to determine maximum and minimum value of Z=x+2y.
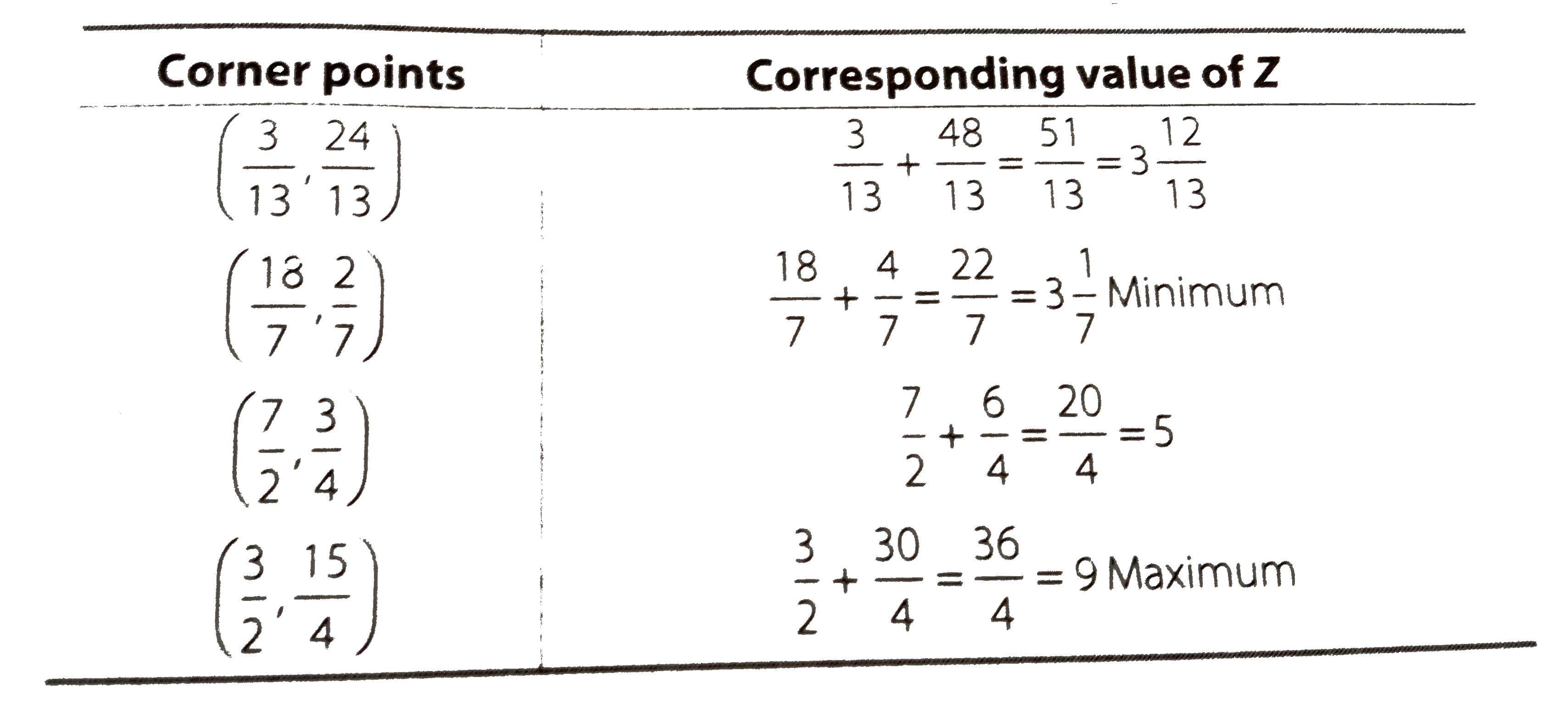
Hence, the maximum and minimum value of Z are 9 and 317, respectively
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - OBJECTIVE
8 Videos
- LINEAR PROGRAMMINGBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - FILLERS
7 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Fillers
18 Videos
- MATRICESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MATRICESEXERCISE - Solved example
101 Videos
Similar Questions
The feasible region for an LPP is shown in following figure. Find the minimum value of Z=11x+7y.

View SolutionFeasible region (shaded) for a LPP is shown in following figure. Maximise Z=5x+7y.

View SolutionIf 'x' be real, find the maximum and minimum value of : y=x+22x2+3x+6
View SolutionIf ∣∣∣z+4z∣∣∣=2,find the maximum and minimum values of |z|.
View SolutionRefers to question 7, maximum value of Z+minimum value of Z is equal to
View SolutionDetermine the maximum value of Z=3x+4y, if the feasible reigon (shaded) for a LPP is shown in following figure
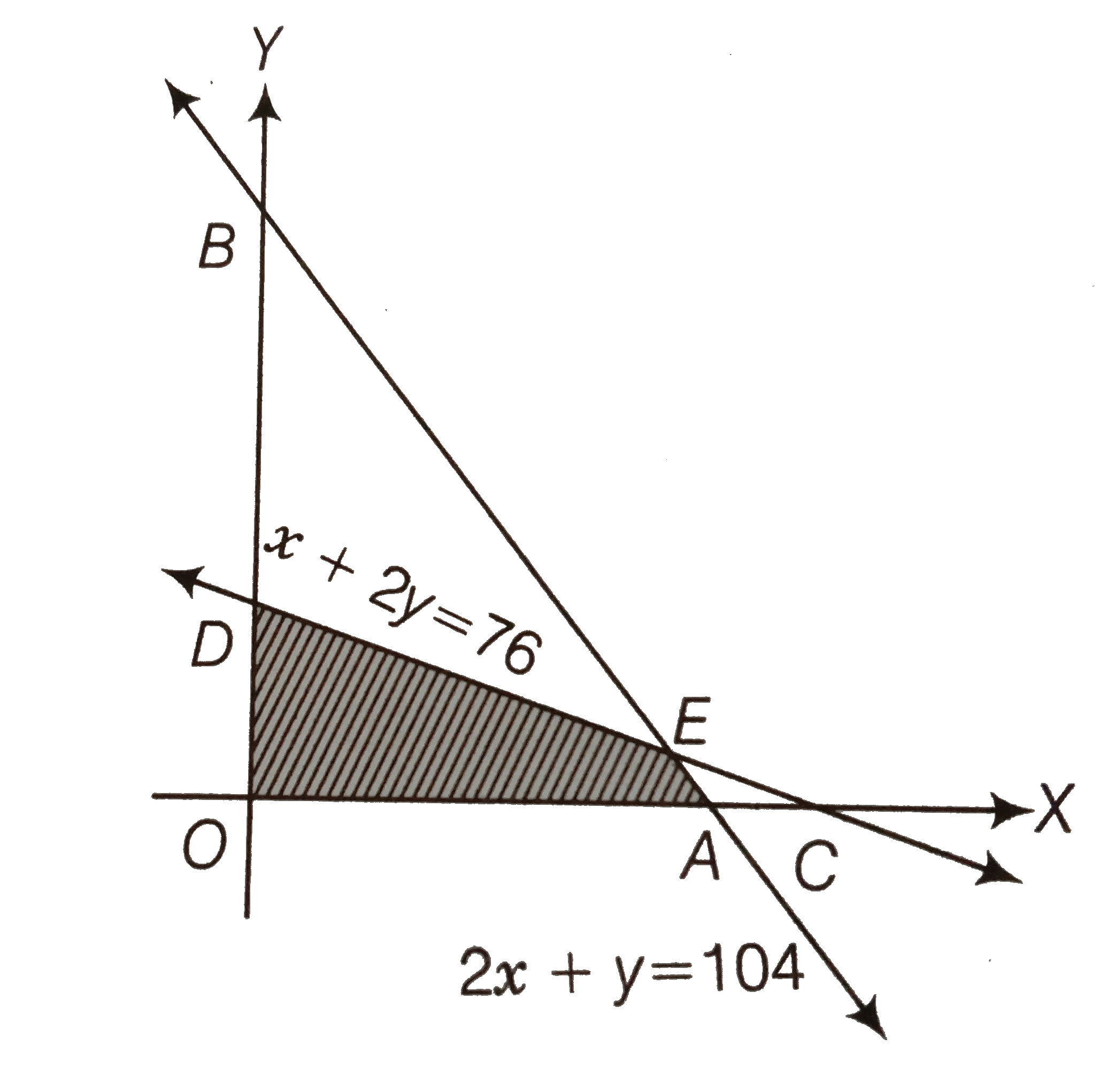
View SolutionIf the feasibile region for a LPP is unbounded, maximum or minimum of the objective function Z = ax + by may or may not exist.
View SolutionIn the given graph,the feasible region for a LPP is shaded. The objective function Z=2x−3y,will be minimum at a) (4,10) b) (6,8) c) (0,8) d) (6,5)
View SolutionA point z moves on the curve |z−4−3i|=2 in an argand plane. The maximum and minimum values of z are
View SolutionFind the maximum and minimum values of |z| satisfying ∣∣∣z+1z∣∣∣=2
View Solution
