Question

The angles of the depression of the top and bottom of the tower is seen from the top of a $60\sqrt{3}$ cliff are ${45}^{\alpha }$ and ${60}^{\alpha }$ respectively. Find the height of the tower.

Explanation

To solve the problem, we need to find the height of the tower given the angles of depression from the top of a cliff. Let's break it down step by step.

Step 1: Understand the Problem
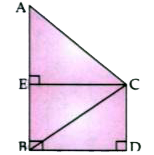
We have a cliff of height \( AD = 60\sqrt{3} \) and a tower \( CE \) whose height we need to find. The angles of depression from the top of the cliff to the top and bottom of the tower are \( 45^\circ \) and \( 60^\circ \) respectively.

Step 2: Draw the Diagram
1. Draw a vertical line representing the cliff \( AD \).
2. Draw the tower \( CE \) below the cliff.
3. Mark point \( B \) at the bottom of the tower and point \( D \) at the base of the cliff.
4. Connect points \( A \) and \( C \) to form the angles of depression.

Step 3: Identify the Angles
- The angle of depression to the top of the tower \( C \) is \( 45^\circ \).
- The angle of depression to the bottom of the tower \( B \) is \( 60^\circ \).

Step 4: Use Trigonometry
1. For angle \( 45^\circ \):
- In triangle \( ABC \):
\( \tan(45^\circ) = \frac{AB}{BC} \)
Since \( \tan(45^\circ) = 1 \):
\( AB = BC \)
Let \( BC = h \) (height of the tower). Then:
\( AB = 60\sqrt{3} - h \)

2. For angle \( 60^\circ \):
- In triangle \( ADE \):
\( \tan(60^\circ) = \frac{AD}{DE} \)
Since \( \tan(60^\circ) = \sqrt{3} \):
\( \sqrt{3} = \frac{60\sqrt{3}}{DE} \)
Rearranging gives:
\( DE = \frac{60\sqrt{3}}{\sqrt{3}} = 60 \)

Step 5: Set Up the Equation
From the first triangle, we have:
\( AB = 60\sqrt{3} - h \)
And from the second triangle, we have:
\( DE = h \)
Thus, substituting \( DE \) into the equation gives:
\( h = 60\sqrt{3} - h \)

Step 6: Solve for \( h \)
1. Rearranging the equation:
\( 2h = 60\sqrt{3} \)
\( h = \frac{60\sqrt{3}}{2} = 30\sqrt{3} \)

Conclusion
The height of the tower \( CE \) is \( 30\sqrt{3} \).