From the top of a 50 m high tower, the angles of depression of the top and bottom of a pole are observed to be 45o and 60o respectively. Find the height of the pole.
To solve the problem, we will use the concept of angles of depression and some basic trigonometry. We have a tower and a pole, and we need to find the height of the pole based on the angles of depression observed from the top of the tower.
Given:
- Height of the tower (h) = 50 m
- Angle of depression to the top of the pole = 45°
- Angle of depression to the bottom of the pole = 60°
1. Understanding the Angles of Depression:
- The angle of depression is the angle formed by the horizontal line from the observer's eye to the object below.
- When we observe the top of the pole, we have an angle of depression of 45°, and for the bottom of the pole, it is 60°.
2. Drawing the Diagram:
- Draw a horizontal line from the top of the tower.
- Mark the tower height (50 m) vertically downwards.
- Mark the position of the pole at a distance 'd' from the base of the tower.
- The height of the pole will be represented as 'h_p'.
3. Using Trigonometry for the Top of the Pole:
- From the top of the tower to the top of the pole, we have:
tan(45°)=Height of tower−Height of poleDistance from tower to pole=50−hpd
- Since tan(45°)=1:
1=50−hpd⟹d=50−hp(Equation 1)
4. Using Trigonometry for the Bottom of the Pole:
- From the top of the tower to the bottom of the pole, we have:
tan(60°)=Height of towerDistance from tower to pole=50d
- Since tan(60°)=√3:
√3=50d⟹d=50√3(Equation 2)
5. Equating the Two Expressions for d:
- From Equation 1 and Equation 2:
50−hp=50√3
6. Solving for h_p:
- Rearranging the equation gives:
hp=50−50√3
- To simplify, multiply the right-hand side by √3√3:
hp=50−50√33
- This can be simplified further:
hp=150−50√33
7. Calculating the Height of the Pole:
- Using the approximate value of √3≈1.732:
hp≈150−50×1.7323≈150−86.63≈63.43≈21.13 m
Final Answer:
The height of the pole is approximately 21.13 meters.
- Height of the tower (h) = 50 m
- Angle of depression to the top of the pole = 45°
- Angle of depression to the bottom of the pole = 60°
- The angle of depression is the angle formed by the horizontal line from the observer's eye to the object below.
- When we observe the top of the pole, we have an angle of depression of 45°, and for the bottom of the pole, it is 60°.
- Draw a horizontal line from the top of the tower.
- Mark the tower height (50 m) vertically downwards.
- Mark the position of the pole at a distance 'd' from the base of the tower.
- The height of the pole will be represented as 'h_p'.
- From the top of the tower to the top of the pole, we have:
tan(45°)=Height of tower−Height of poleDistance from tower to pole=50−hpd
- Since tan(45°)=1:
1=50−hpd⟹d=50−hp(Equation 1)
- From the top of the tower to the bottom of the pole, we have:
tan(60°)=Height of towerDistance from tower to pole=50d
- Since tan(60°)=√3:
√3=50d⟹d=50√3(Equation 2)
- From Equation 1 and Equation 2:
50−hp=50√3
- Rearranging the equation gives:
hp=50−50√3
- To simplify, multiply the right-hand side by √3√3:
hp=50−50√33
- This can be simplified further:
hp=150−50√33
- Using the approximate value of √3≈1.732:
hp≈150−50×1.7323≈150−86.63≈63.43≈21.13 m
The height of the pole is approximately 21.13 meters.
Topper's Solved these Questions
Similar Questions
From the top of a building AB , 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30o and 60o respectively. Find the height of the lamp post.
View SolutionFrom the top of a cliff, the angle of depression of the top and bottom of a tower are observed to be 45∘ and 60∘ respectively. If the height of the tower is 20 m.
Find :
(i) the height of the cliff
(ii) the distance between the cliff and the tower.
View SolutionFrom the top of a building AB , 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30o and 60o respectively. Find the difference between the heights of the building and the lamp post.
View SolutionFrom the top of a building 60m high the angles of depression of the top and the bottom of a tower are observed to be 30o and 60o . Find the height of the tower.
View SolutionFrom the top of a building AB , 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30o and 60o respectively. Find the horizontal distance between AB and CD
View SolutionFrom te top of a tower , 60 meters high, the angles of depression of the top and bottom of a pole are αandβ respectively .Find the height of the pole.
View SolutionA vertical tower 50ft high stands on a sloping groud. The foot of the tower is at the same level as the middle point of a vertical flag pole. From the top of the tower the angle of depression of the top and the bottom of the pole are 15∘ and 45∘ respectively. Find the length of the pole.
View SolutionIn the figure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30∘and60∘ respectively. Find :
(ii) the height of the lamp post.
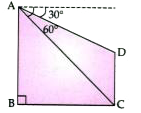
View SolutionIn the given figure, A from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30∘and60∘ respectively. Find :
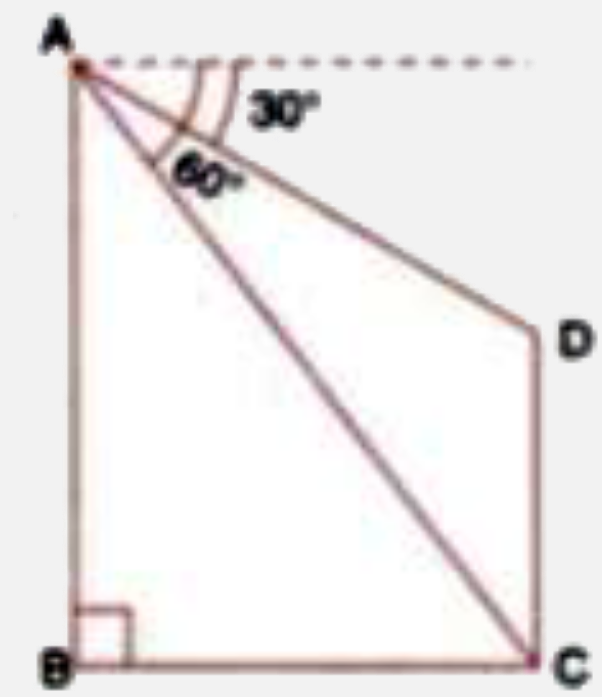
the horizontal distance between AB and CD
View SolutionIf from the top of a tower 80 meters high the angles of depression of the top and bottom of a house are 30∘and45∘ respectively, then the height of the house is
View Solution
