The graph of y=p(x), where p(x) is a polynomial in variable x, is as follows:
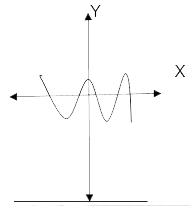
The number of zeroes of p(x) is _______________
5
Topper's Solved these Questions
- SAMPLE PAPER 2019BOOK - X BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - 29A
1 Videos
- SAMPLE PAPER 2019BOOK - X BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION-A (FILL IN THE BLANKS)
3 Videos
- SAMPLE PAPER 2019BOOK - X BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - 12A
1 Videos
- CBSE BOARDS 2020BOOK - X BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - CBSE BOARDS 2020EXERCISE - QUESTION
41 Videos
- X BoardsBOOK - X BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - X BoardsEXERCISE - All Questions
481 Videos
Similar Questions
The following figure shows the graph of y=p(x), where p(x) is a polynomial in variable x. The number of zeroes of the polynomial p(x) is
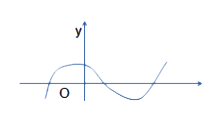
View SolutionLook at the graphs in Figure given below. Each is the graph of y=p(x), where p(x) is a polynomial. For each of the graphs, find the number of zeroes of p(x).
View Solution
Knowledge Check
For a polynomial p(x), the value of p(3) is −2.
Which of the following must be true about p(x) ?Ax−5 is a factor of p(x).Bx−2 is a factor of p(x).Cx+2 is a factor of p(x).DThe remainder when p(x) is divided by x−3 is−2.
The graphs of y=p(x)are given in Figure below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.
View SolutionIn Figure, the graph of a polynomial p(x) is shown. The number of zeroes of p(x) is (a)4 (b) 1 (c) 2 (d) 3
View SolutionThe graph of a polynomial y=f(x) , shown in Fig. 2.18. Find the number of real zeros of f(x) . (FIGURE)
View Solution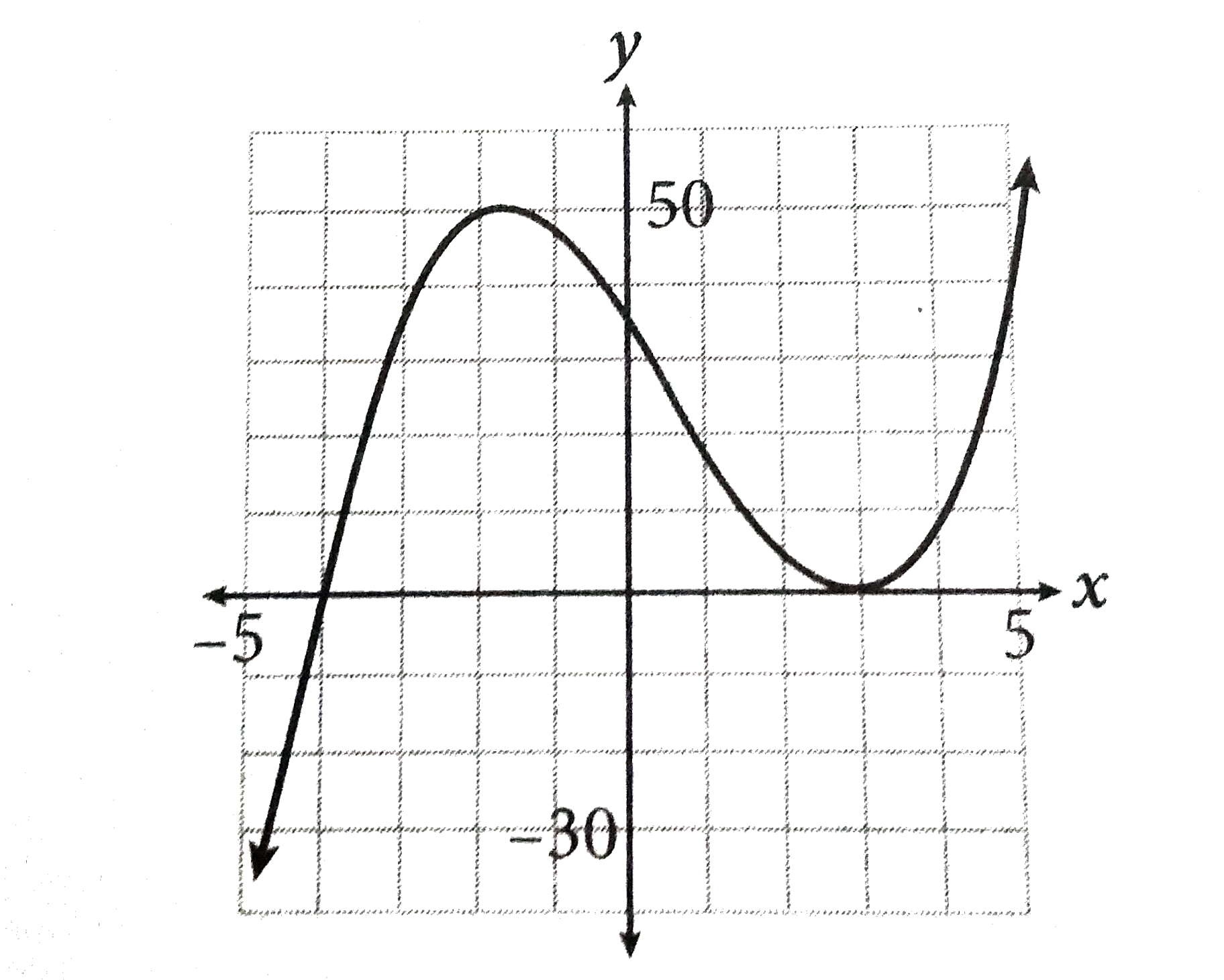
If p(x) is the polynomial functions shown in the graph above, which of the following could be fractored form of p(x)?
View SolutionIf 1 is a zero of the polynomial p(x)=ax2—3(a—1)x−1, then find the value of a.
View SolutionZero of the polynomial p(x)=2x+5 is
View SolutionLet P(x)=x10+a2x8+a3x6+a4x4+a5x2 be a polynomial with real coefficients. If P(1)=1andP(2)=−5, then the minimum-number of distinct real zeroes of P(x) is
View Solution
