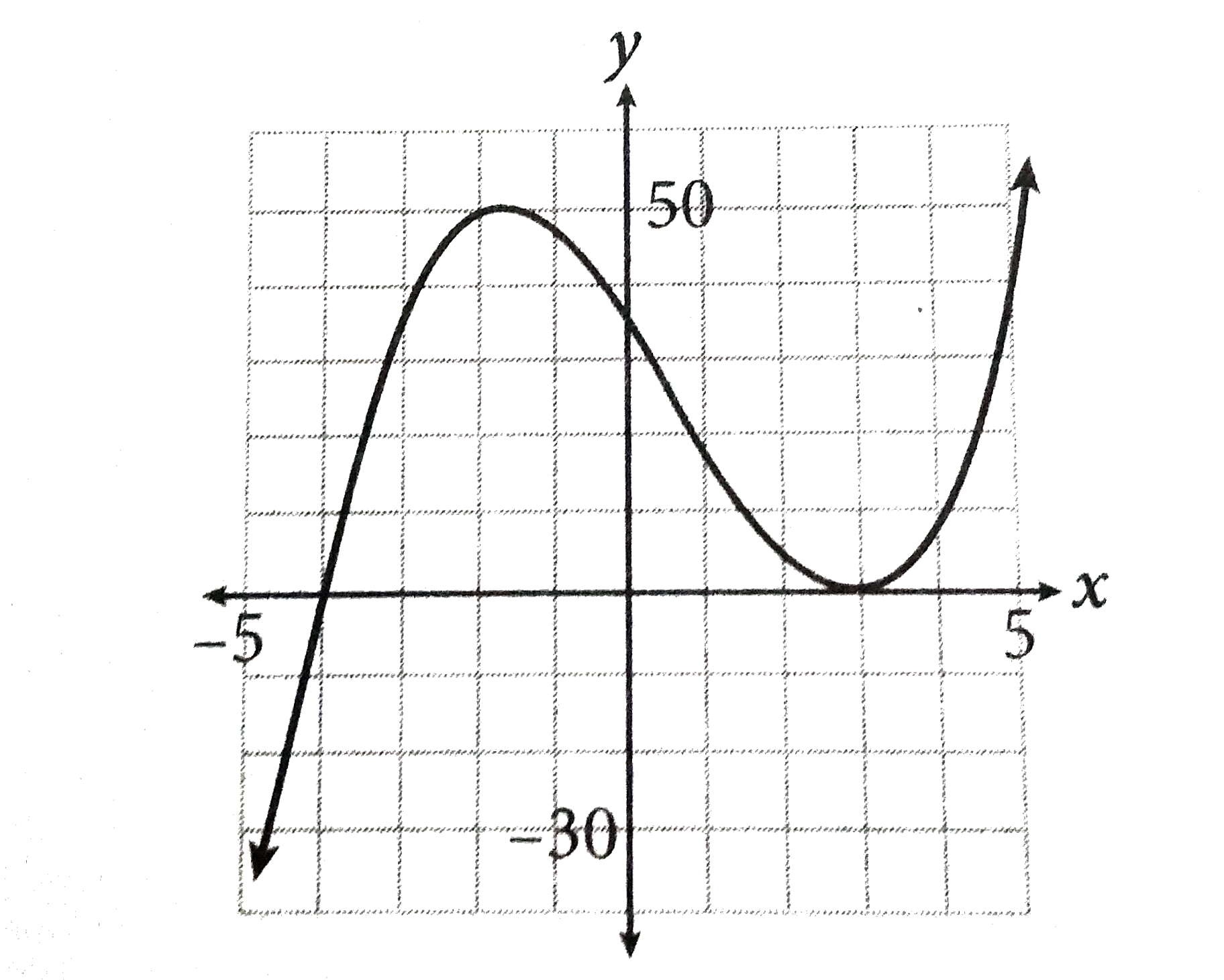
If p(x) is the polynomial functions shown in the graph above, which of the following could be fractored form of p(x)?
A
p(x)=(x−4)(x+3)
B
p(x)=(x−4)(x+3)2
C
p(x)=(x+4)(x−3)
D
p(x)=(x+4)(x−3)2
Video Solution
Text Solution
The correct Answer is:D
Difficult:Easy
Category: Passport to Advanced Math/ Functions
Strategic Advice: The graph of a polynomial function crosses the x-axis when there is a single root and just touches the x-axis when there is a double root. A double roots occurs when a factor is repreated, or in other word, is raised to the second power. For example, the factor (x-a) produces a single root at x=a,while (x−a)2 produces a double root at x=b.
Getting to the Answer: Examine the graph. The function crosses the x-axis at x=-4, which means one factor is (x−(−4)), or (x+4). This means you can eliminate A and B. The function just touches the x-axis at x=3, which means the other factor (which should be raised to the seconnd power) is x-3. The factored form of the polynomial could be p(x)=(x+4)(x−3)2, which is (D).
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following could be the graph of y=3−2x ?
A B
B C
C D
D
- Question 2 - Select One
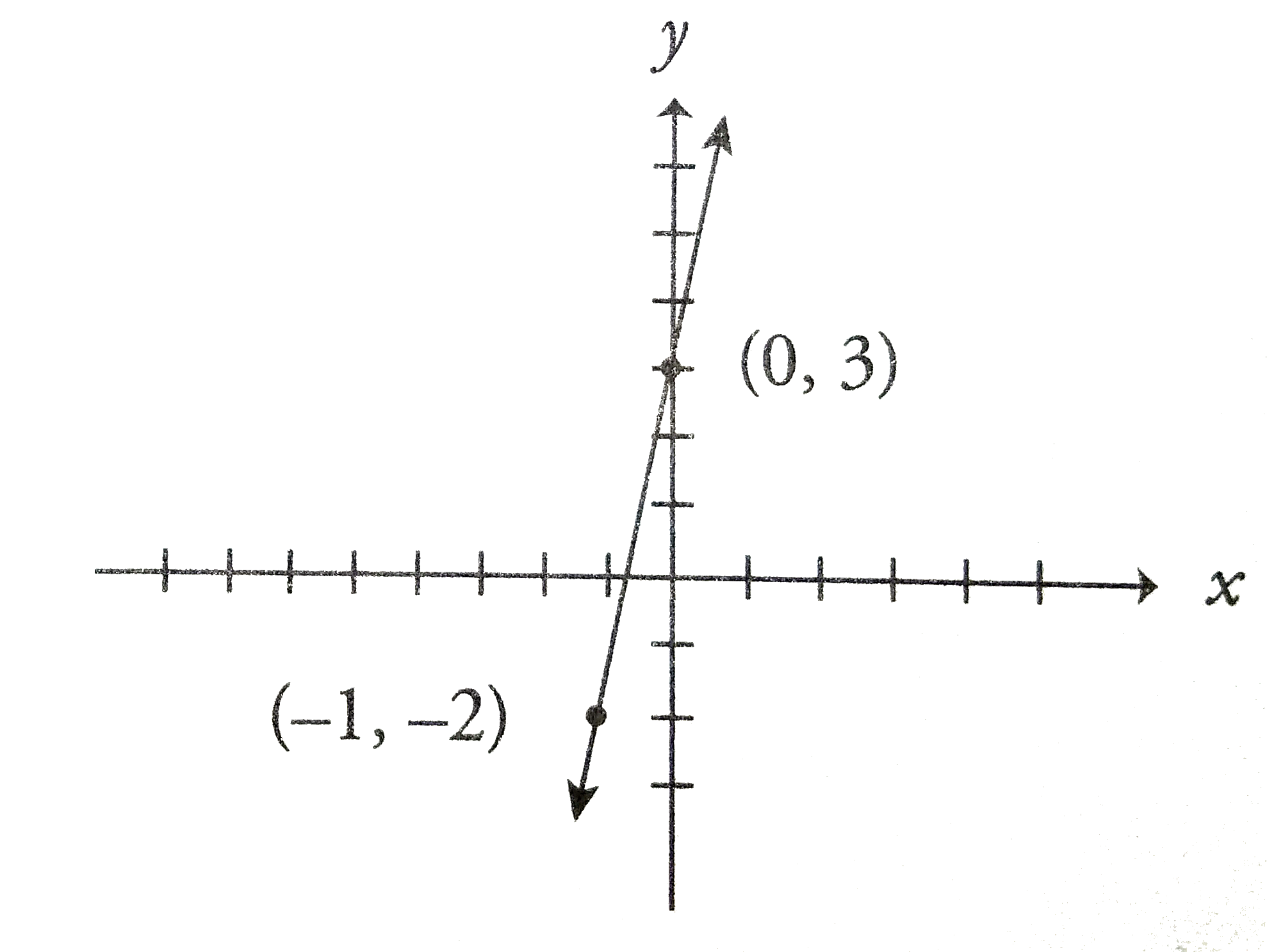
If the graph above is that of f(x), which of the following could be f(x)?Af(x)=15x+15Bf(x)=15x+3Cf(x)=3x+5Df(x)=5x+3 - Question 3 - Select One
Which of the following could be the graph of 2x+3y+12=0 ?
A B
B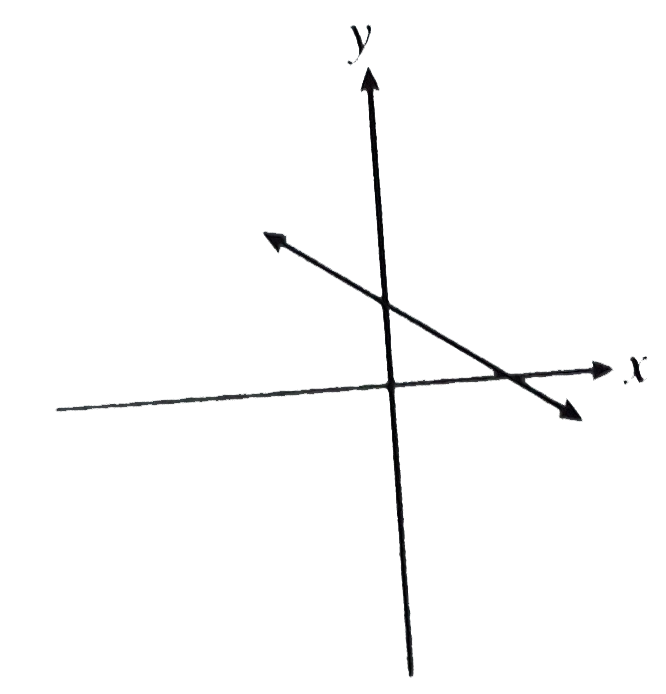 C
C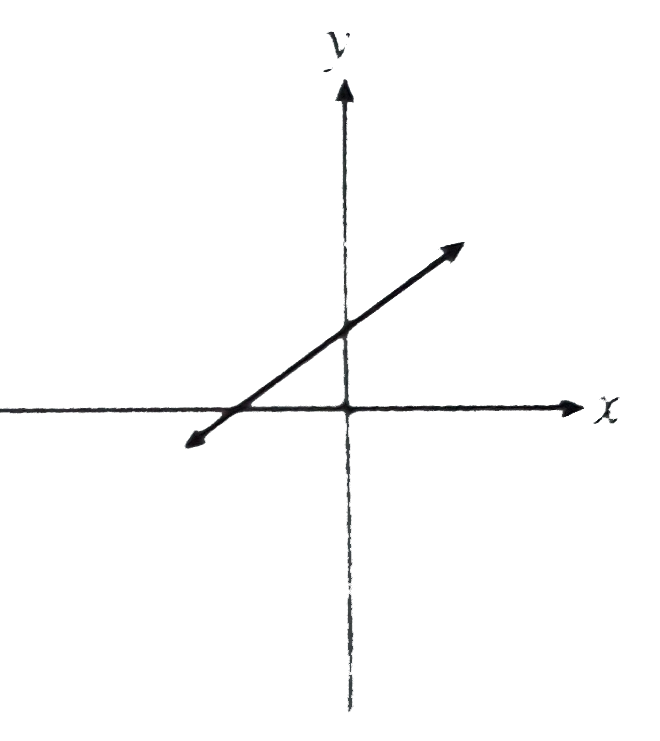 D
D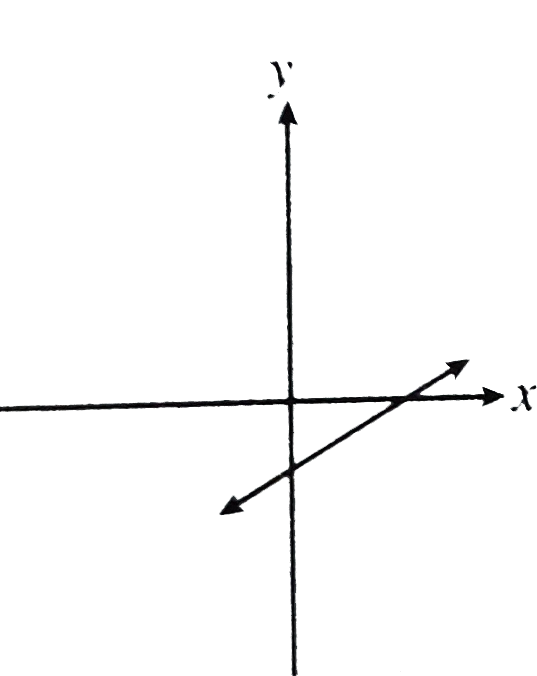
If p(x) is a polynomial function with p(3)=0, which statement must be true?
View Solution
The graph of the function f is shown above. Which of the following could represent the graph of y=|f(x)|?View Solution
The function f is defined by a polynomial. Some values of x and f x( ) are shown in the table above. Which of the following must be a factor of f x( ) ?View Solution
The function g is defined by a polynomial some of the value of x and g(x) are shown in the table above. Which of the following must be factor of g?View SolutionIf p(x) is a polynomial function and p(4)=0, then which statement is true?
View Solution


