It is desired to obtain an erect image of an object, using concave mirror of focal length of 12 cm.
(i) What should be the range of distance of an object placed in front of mirror ?
(ii) Will the image be smaller or large than the object ? Draw a ray diagram to show the formation of image in this case.
(iii) Where will the image of this object be, if it is placed 24 cm in front of the mirror ? Draw a ray diagram for this situation also to justify your answer.
Show the positions of the pole, the principal focus and the centre of curvature in the above ray diagrams.
To solve the question step by step, we will break it down into its parts as follows:
Part (i): Range of Distance of the Object
1. Understanding the Concave Mirror: A concave mirror can produce an erect image only when the object is placed between the focus (F) and the mirror (P). The focal length (F) is given as -12 cm (negative because it is a concave mirror).
2. Identifying the Range:
- The focus (F) is at -12 cm.
- The object must be placed between the focus and the mirror, which means the object distance (u) must be greater than the focal length but less than the distance of the mirror (P).
- Therefore, the range of the object distance is:
−12<u<0 cm
- This means the object should be placed anywhere between 0 cm (the mirror) and -12 cm (the focus).
Part (ii): Size of the Image
1. Image Characteristics: When the object is placed between the focus and the mirror, the image formed is virtual and erect.
2. Comparison of Sizes: The image formed is larger than the object. This can be understood from the nature of the ray diagram:
- Rays parallel to the principal axis reflect through the focus.
- Rays passing through the center of curvature reflect back on themselves.
- The intersection of these rays forms a virtual image that is larger than the object.
Part (iii): Image Position for Object at 24 cm
1. Using the Mirror Formula: The mirror formula is given by:
1f=1v+1u
Where:
- f=−12 cm (focal length)
- u=−24 cm (object distance, negative as per sign convention)
2. Substituting Values:
1−12=1v+1−24
3. Finding v:
- Rearranging gives:
1v=1−12+124
- Finding a common denominator (24):
1v=−224+124=−124
- Thus,
v=−24 cm
4. Conclusion: The image is formed at -24 cm, which indicates that it is real and located on the same side as the object.
Ray Diagrams
1. Ray Diagram for Part (i):
- Draw a concave mirror with the principal axis.
- Mark the focus (F) at -12 cm and the pole (P) at 0 cm.
- Show the object placed between P and F.
- Draw rays: one parallel to the principal axis reflecting through F, and one through the center of curvature reflecting back.
2. Ray Diagram for Part (iii):
- Draw the same concave mirror.
- Mark the object at -24 cm.
- Draw rays: one parallel to the principal axis reflecting through F, and one through the center of curvature.
- Show that the rays converge at -24 cm, indicating a real image.
- The focus (F) is at -12 cm.
- The object must be placed between the focus and the mirror, which means the object distance (u) must be greater than the focal length but less than the distance of the mirror (P).
- Therefore, the range of the object distance is:
−12<u<0 cm
- This means the object should be placed anywhere between 0 cm (the mirror) and -12 cm (the focus).
- Rays parallel to the principal axis reflect through the focus.
- Rays passing through the center of curvature reflect back on themselves.
- The intersection of these rays forms a virtual image that is larger than the object.
1f=1v+1u
Where:
- f=−12 cm (focal length)
- u=−24 cm (object distance, negative as per sign convention)
1−12=1v+1−24
- Rearranging gives:
1v=1−12+124
- Finding a common denominator (24):
1v=−224+124=−124
- Thus,
v=−24 cm
- Draw a concave mirror with the principal axis.
- Mark the focus (F) at -12 cm and the pole (P) at 0 cm.
- Show the object placed between P and F.
- Draw rays: one parallel to the principal axis reflecting through F, and one through the center of curvature reflecting back.
- Draw the same concave mirror.
- Mark the object at -24 cm.
- Draw rays: one parallel to the principal axis reflecting through F, and one through the center of curvature.
- Show that the rays converge at -24 cm, indicating a real image.
Similar Questions
We wish to obtain an erect image of an object, using a concave mirror of focal length 15 cm. What should be the range of distance of the object from the mirror? What is the nature of the image? Is the image larger or smaller than the object? Draw a ray diagram to show the image formation in this case.
View SolutionDraw a ray diagram showing the formation of image of a point object by a plane mirror.
View SolutionAn object is placed in front of a converging lens at a distance greater than twice the focal length of the lens. Draw a ray diagram to show the formation of the image.
View SolutionAn object is kept 40 cm in front of a concave mirror of focal length of 20 cm. Find the position and nature of the image. Draw a ray diagram to show the formation of image in this case.
View SolutionAn object is placed at a distance of 20 cm from a concave mirror of focal lenght 10 cm. What is the image distance?
View SolutionAn object is placed 40 cm from a concave mirror of focal length 20 cm. The image formed is
View SolutionThe image formed by a convex mirror of focal length 30cm. is a quarter of the object. What is the distance of the object from the mirror ?
View SolutionFig. shows a concave mirror with its pole at P, focus F and centre of curvature C. Draw ray diagram to show the formation of image of an object OA.
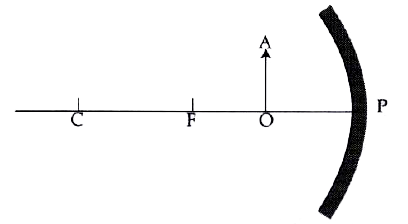 View Solution
View SolutionA converging lens is used to obtain an image of an object placed in front of it. The inverted image is formed between F2and2F2 of the lens.
Draw a ray diagram to illustrate the formation of the image obtained.View SolutionDraw a ray diagram to show the formation of image by a concave mirror for an object beyond its centre of curvature. State three characteristics of the image.
View Solution

