While traching the path of a ray of light passing through a rectangular glass slab a student tabulated his observations. If in his experiment for two readings he takes two values of ∠ians40∘and50∘ . What should be the correct values of ∠eand∠r in each case ?
To solve the problem of finding the angles of refraction (R) and emergence (E) for the given angles of incidence (I) of 40° and 50° when light passes through a rectangular glass slab, we can follow these steps:
1. Identify the Refractive Index (μ):
- The refractive index for glass is given as 1.5.
2. Use Snell's Law:
- Snell's Law states that:
sinIsinR=μ
- Rearranging gives:
sinR=sinIμ
3. Calculate for the First Angle of Incidence (I = 40°):
- Calculate sinR:
sinR=sin40°1.5
- Using sin40°≈0.6428:
sinR=0.64281.5≈0.4285
- Find angle R:
R=sin−1(0.4285)≈25.37°
- Since the angle of emergence (E) is equal to the angle of incidence (I):
E=40°
4. Calculate for the Second Angle of Incidence (I = 50°):
- Calculate sinR:
sinR=sin50°1.5
- Using sin50°≈0.7660:
sinR=0.76601.5≈0.5107
- Find angle R:
R=sin−1(0.5107)≈30.7°
- Again, the angle of emergence (E) is equal to the angle of incidence (I):
E=50°
Summary of Results:
- For I = 40°:
- Angle of Refraction (R) = 25.37°
- Angle of Emergence (E) = 40°
- For I = 50°:
- Angle of Refraction (R) = 30.7°
- Angle of Emergence (E) = 50°
- The refractive index for glass is given as 1.5.
- Snell's Law states that:
sinIsinR=μ
- Rearranging gives:
sinR=sinIμ
- Calculate sinR:
sinR=sin40°1.5
- Using sin40°≈0.6428:
sinR=0.64281.5≈0.4285
- Find angle R:
R=sin−1(0.4285)≈25.37°
- Since the angle of emergence (E) is equal to the angle of incidence (I):
E=40°
- Calculate sinR:
sinR=sin50°1.5
- Using sin50°≈0.7660:
sinR=0.76601.5≈0.5107
- Find angle R:
R=sin−1(0.5107)≈30.7°
- Again, the angle of emergence (E) is equal to the angle of incidence (I):
E=50°
- For I = 40°:
- Angle of Refraction (R) = 25.37°
- Angle of Emergence (E) = 40°
- Angle of Refraction (R) = 30.7°
- Angle of Emergence (E) = 50°
Similar Questions
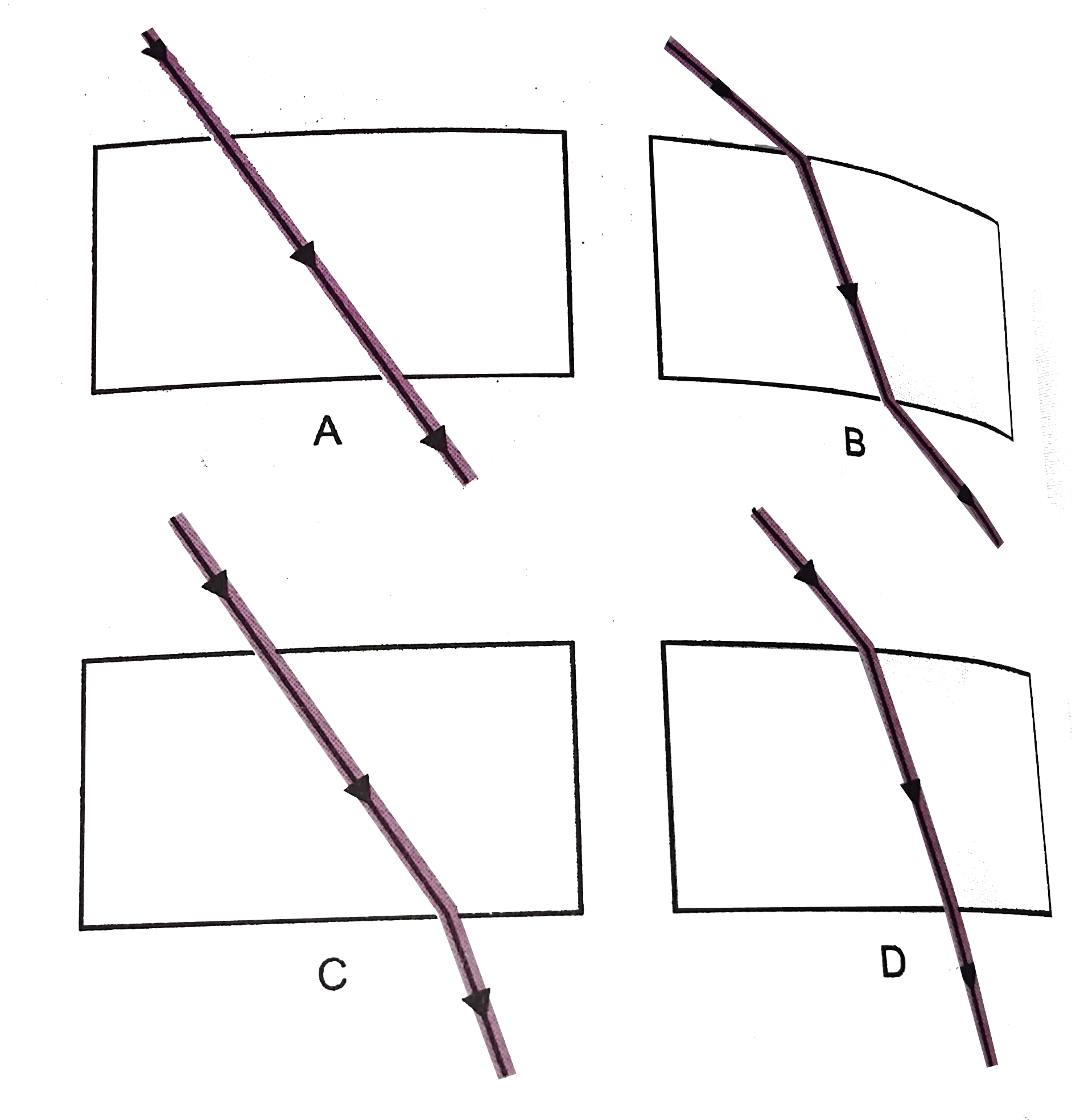
The path of a ray light coming from air passing through a rectangular glass slab traced by four students are shown as A, B, C and D in Figure. Which one of them is correct ?
View SolutionA ray of light strikes the surface of a rectangular glass slab such that the angle of incidence in air is (i) 0∘,(ii)45∘. In each case, draw a diagram to show the path taken by the ray as it passes through the glass slab and emerges from it.
View Solution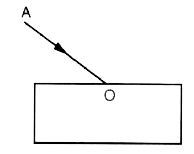
In the adjacent diagram, AO is a ray of light incident on a rectangular glass slab.
(a) Complete the path of the ray till it emerges out of the slab.
(b) In the diagram, mark the angle of incidence (i) and the angle of refraction (r) at the first interface. how is the refractive index of glass related to the angles i and r ?
(c) Mark angle of emergence by the letter e. how are the angles i and e related ?
(d) Which two rays are parallel to each other ? Name them
(e) Indicate in the diagram the lateral displacement between the emergent ray and the incident ray. state one factor that affects the lateral displacement.
View SolutionDiagram (a) and (b) in figure below show the refraction of a ray of light of single colour through a prism and a parallel sided glass slab respectively.
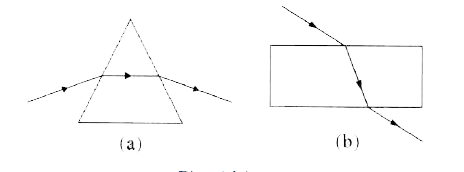
(i) In each diagram, label the incident, refracted, emergent rays and the angle of deviation.
(ii) In what way the direction of the emergent ray in the two cases differ with respect to the incident ray ? explain your answer.
View Solution(a) A student suffering from myopia is not able to see distinctly the objects placed beyond 5m. Two possible reasons due to which this defect of vision may have arisen. With the help of ray diagrams, explain :
(i) Why the student is unable to see distinctly the objects placed beyond 5m from his eyes.
(ii) The type of corrective lens used to restore proper vision and how this defect is corrected by the use of this lens.
(b) If in this case, numerical value of focal length of corrective lens is 5m, find the power of the lens as per the new cartesion sign convention.
View SolutionMohan was asked by his teacher to determine the boiling point of a liquid. He set up the apparatus as shown in the figure. He recorded the boiling point of the liquid as 140∘C and reported the reading to this teacher. The teacher asked him to repeat the experiment after dipping the bulb of the thermometer in the liquid and also placing the beaker on a tripod stand covered with a wire gauze. After reading this narration, answer the following question :
(i) Was the reading taken by the student correct ?
(ii) What was the necessity of wire gauze?
(iii) How did teacher help the student?
(iv) What is teh value based information associated with this?

View SolutionYoung's double-slit experiment setup with ligth of wavelength λ=6000Å, distance between two slit in 2 mm and distance between the plane of slits and the screen. Is 2 m. The slits are of equal intensity. When a sheet of glass of refractive index 1.5 (which permtis only a fraction η of the incident light to pass through) and thickness 8000Å is placed in front of the lower slit, it is observed that the intensity at a point P, 0.15 mm above the central maxima, does not change.
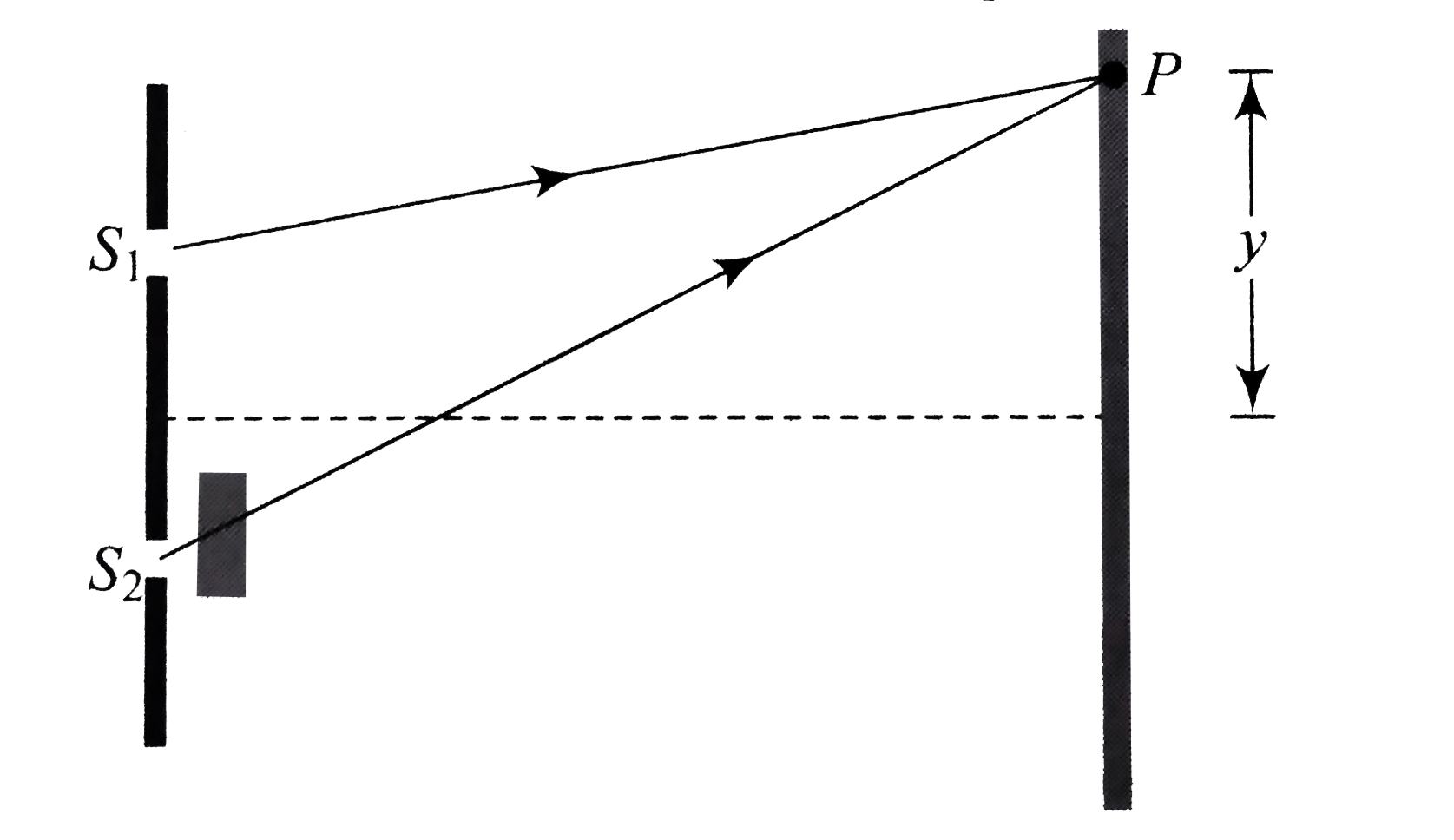
The value of η is
View SolutionThe existence of negatively charged particle in an atom was shown by J.J. Thomson as a result of the studies of the passage of electricity through gases at extremely low pressure known as discharge tube experiments. When a high voltage of the order of 10,000 volts or more was impressed across the electrodes, some sort of invisible rays moved from the negative electrode to the positive electrode these rays are called as cathode rays.
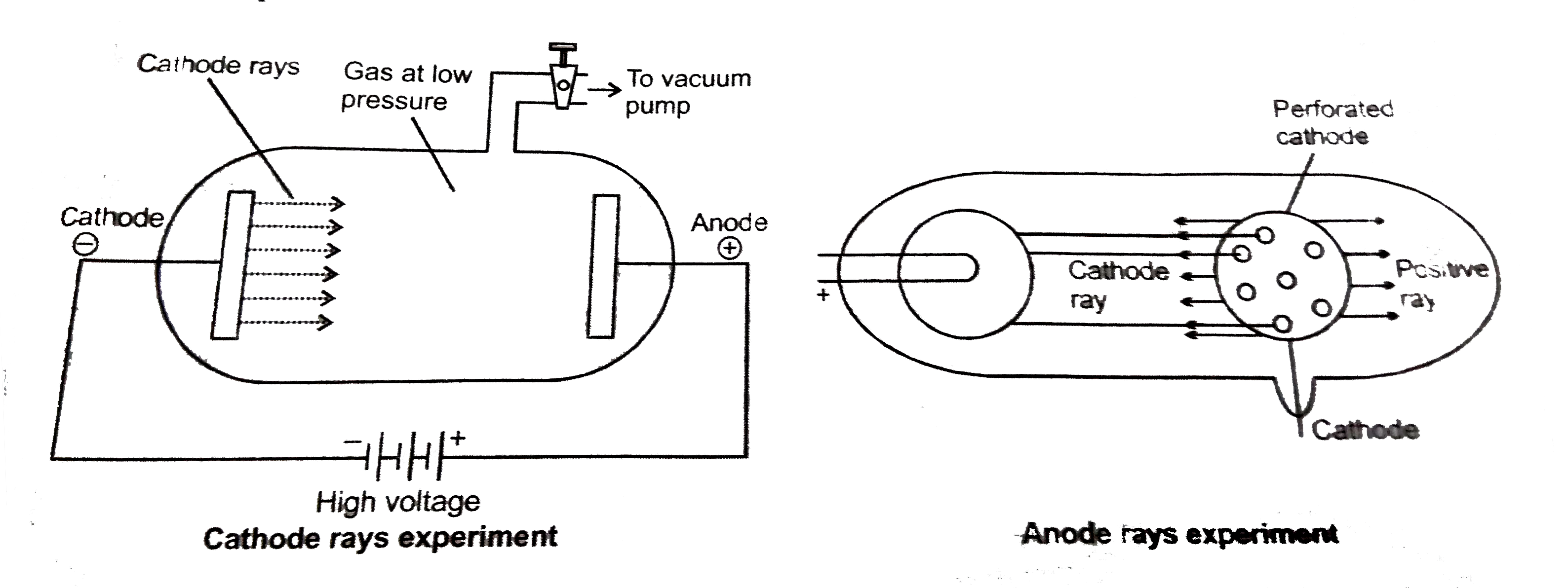
Cathode rays travel in straight path in absence of electrical and magnetic field . Cathode rays consist of material part and charged particles? Cathode rays produce X-rays and light is emitted when they strike on ZnS screen. Cathode rays penetrate through thin sheets of aluminium and other metals . They affect the photogenic plate and passes heating effect when they strike on metal foil. The raito of charge to mass i.e charge/mass is same for all the cathode rays irrespective of the gas used in the tube.
The existence of positively charged particle in an atom was shown be E. Goldstein. He repeated the same discharge tube experiments by using a perforated cathode. It was observed that when a high potential difference was applied between the electrodes, not only cathode rays were produced but also a new type of rays were produced simultaneoulsy from anode moving towards cathode and passes through the holes or canal of the cathode. These termed as canal rays or anode rays.
These rays travel in straight lines and consists of positively charged particles. These rays have kinetic energy and produces heating effect also. The e/m ratio of these rays is smaller than that of electrons. Unlike cathode rays, their e/m value is dependent upon the nature of the gas taken in the tube. These rays produced flashes of light on ZnS screen and can pass throughs thin metal foils. They can produce physical and chemical changes and are capable to produce ionisation in gases.
For cathode rays the value of e/m:
View SolutionThe existence of negatively charged particle in an atom was shown by J.J. Thomson as a result of the studies of the passage of electricity through gases at extremely low pressure known as discharge tube experiments. When a high voltage of the order of 10,000 volts or more was impressed across the electrodes, some sort of invisible rays moved from the negative electrode to the positive electrode these rays are called as cathode rays.
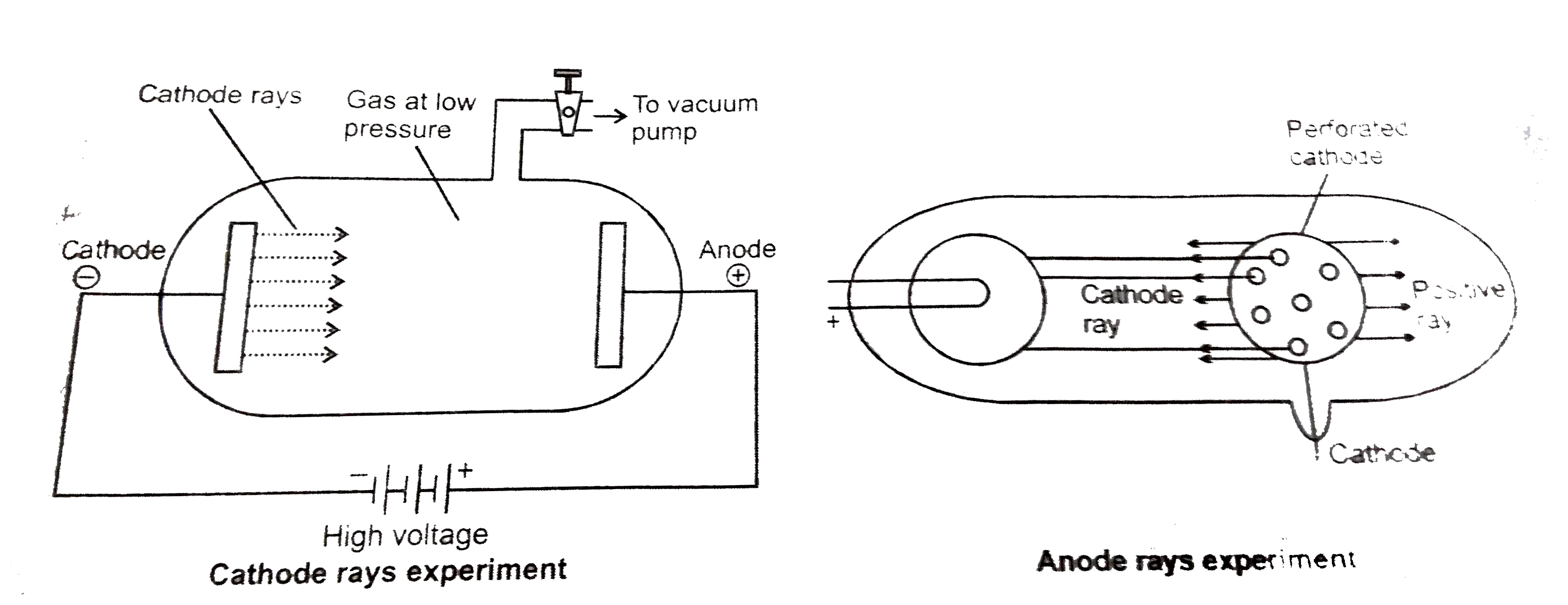
Cathode rays travel in straight path in absence of electrical and magnetic field . Cathode rays consist of material part and charged particles? Cathode rays produce X-rays and light is emitted when they strike on ZnS screen. Cathode rays penetrate through thin sheets of aluminium and other metals . They affect the photogenic plate and passes heating effect when they strike on metal foil. The raito of charge to mass i.e charge/mass is same for all the cathode rays irrespective of the gas used in the tube.
The existence of positively charged particle in an atom was shown be E. Goldstein. He repeated the same discharge tube experiments by using a perforated cathode. It was observed that when a high potential difference was applied between the electrodes, not only cathode rays were produced but also a new type of rays were produced simultaneoulsy from anode moving towards cathode and passes through the holes or canal of the cathode. These termed as canal rays or anode rays.
These rays travel in straight lines and consists of positively charged particles. These rays have kinetic energy and produces heating effect also. The e/m ratio of these rays is smaller than that of electrons. Unlike cathode rays, their e/m value is dependent upon the nature of the gas taken in the tube. These rays produced flashes of light on ZnS screen and can pass throughs thin metal foils. They can produce physical and chemical changes and are capable to produce ionisation in gases.
Which is not true with respect to cathode rays?
View SolutionThe existence of negatively charged particle in an atom was shown by J.J. Thomson as a result of the studies of the passage of electricity through gases at extremely low pressure known as discharge tube experiments. When a high voltage of the order of 10,000 volts or more was impressed across the electrodes, some sort of invisible rays moved from the negative electrode to the positive electrode these rays are called as cathode rays.
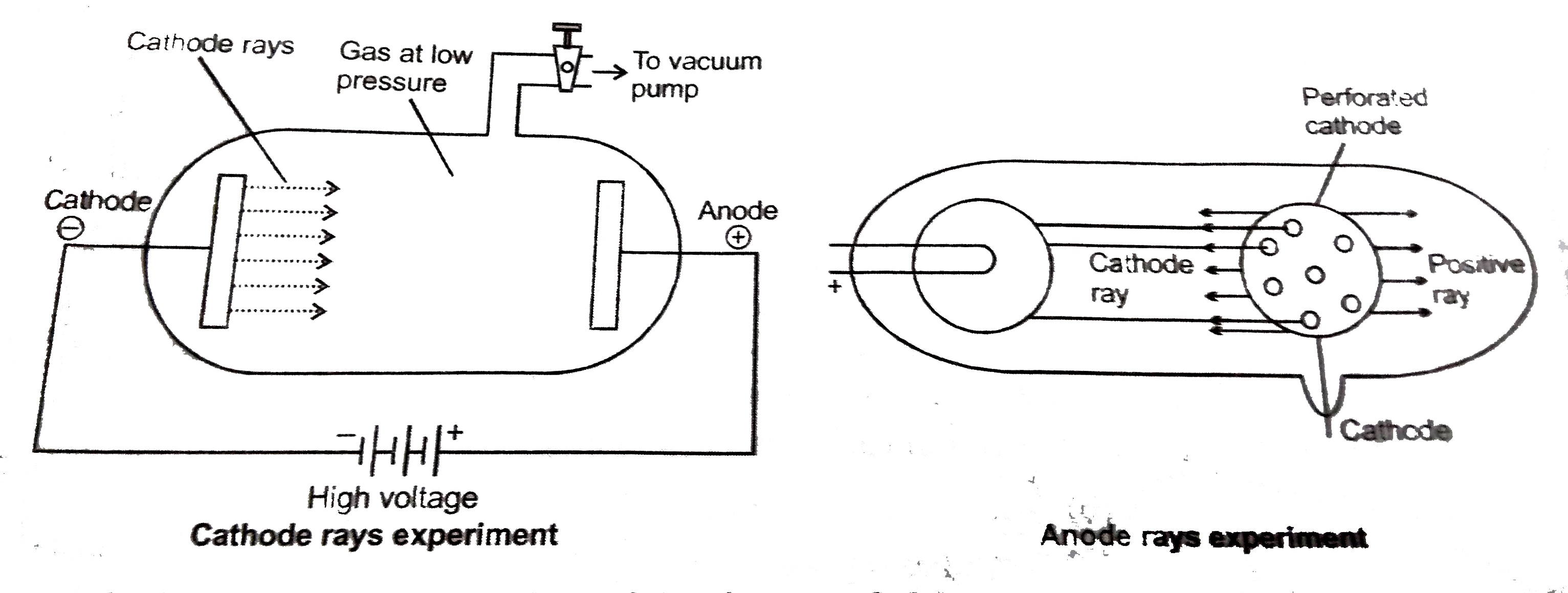
Cathode rays travel in straight path in absence of electrical and magnetic field . Cathode rays consist of material part and charged particles? Cathode rays produce X-rays and light is emitted when they strike on ZnS screen. Cathode rays penetrate through thin sheets of aluminium and other metals . They affect the photogenic plate and passes heating effect when they strike on metal foil. The raito of charge to mass i.e charge/mass is same for all the cathode rays irrespective of the gas used in the tube.
The existence of positively charged particle in an atom was shown be E. Goldstein. He repeated the same discharge tube experiments by using a perforated cathode. It was observed that when a high potential difference was applied between the electrodes, not only cathode rays were produced but also a new type of rays were produced simultaneoulsy from anode moving towards cathode and passes through the holes or canal of the cathode. These termed as canal rays or anode rays.
These rays travel in straight lines and consists of positively charged particles. These rays have kinetic energy and produces heating effect also. The e/m ratio of these rays is smaller than that of electrons. Unlike cathode rays, their e/m value is dependent upon the nature of the gas taken in the tube. These rays produced flashes of light on ZnS screen and can pass throughs thin metal foils. They can produce physical and chemical changes and are capable to produce ionisation in gases.
Select the incorrect statement.
View Solution
