Young's double-slit experiment setup with ligth of wavelength λ=6000Å, distance between two slit in 2 mm and distance between the plane of slits and the screen. Is 2 m. The slits are of equal intensity. When a sheet of glass of refractive index 1.5 (which permtis only a fraction η of the incident light to pass through) and thickness 8000Å is placed in front of the lower slit, it is observed that the intensity at a point P, 0.15 mm above the central maxima, does not change.
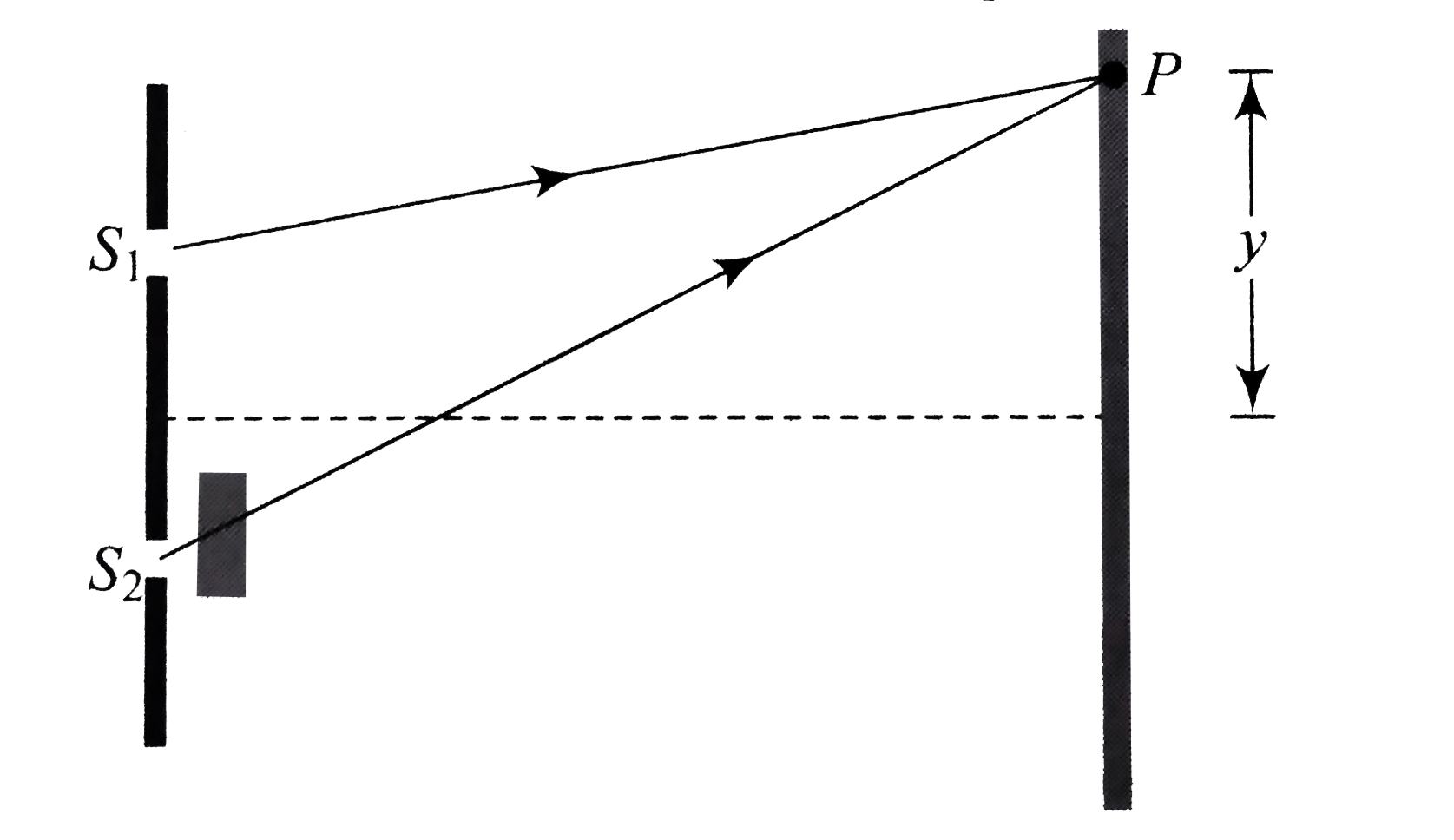
The value of η is
0.21
0.42
0.12
0.5
The correct Answer is:a
Without inserting the slab, path difference at P,
Δx=ydD=0.15×10−3×2×10−32=1.5×10−7m
Corresponding phase difference at P,
ϕ=(2πλ)(Δx)
=(2π6000×10−10)(1.5×10−7)=π2
ϕ2=π4
Therefore, intensity at P,
I=4I0cos2(ϕ/2)=2I0
Phase difference after placing to glass sheet,
ϕ'=ϕ+2πλ(μ−1)t
=π2+2π6000×10−10(1.5−1)(8000×10−19)
=11π6
Now, the intensity at P is,
I'=I0+ηI0+2√ηI20cos.11π6=2I0 (given)
solving this equation, we get η=0.21.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Integer
3 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Archives
4 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning
13 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
Young's double-slit experiment setup with ligth of wavelength λ=6000Å, distance between two slit in 2 mm and distance between the plane of slits and the screen. Is 2 m. The slits are of equal intensity. When a sheet of glass of refractive index 1.5 (which permtis only a fraction η of the incident light to pass through) and thickness 8000Å is placed in front of the lower slit, it is observed that the intensity at a point P, 0.15 mm above the central maxima, does not change.
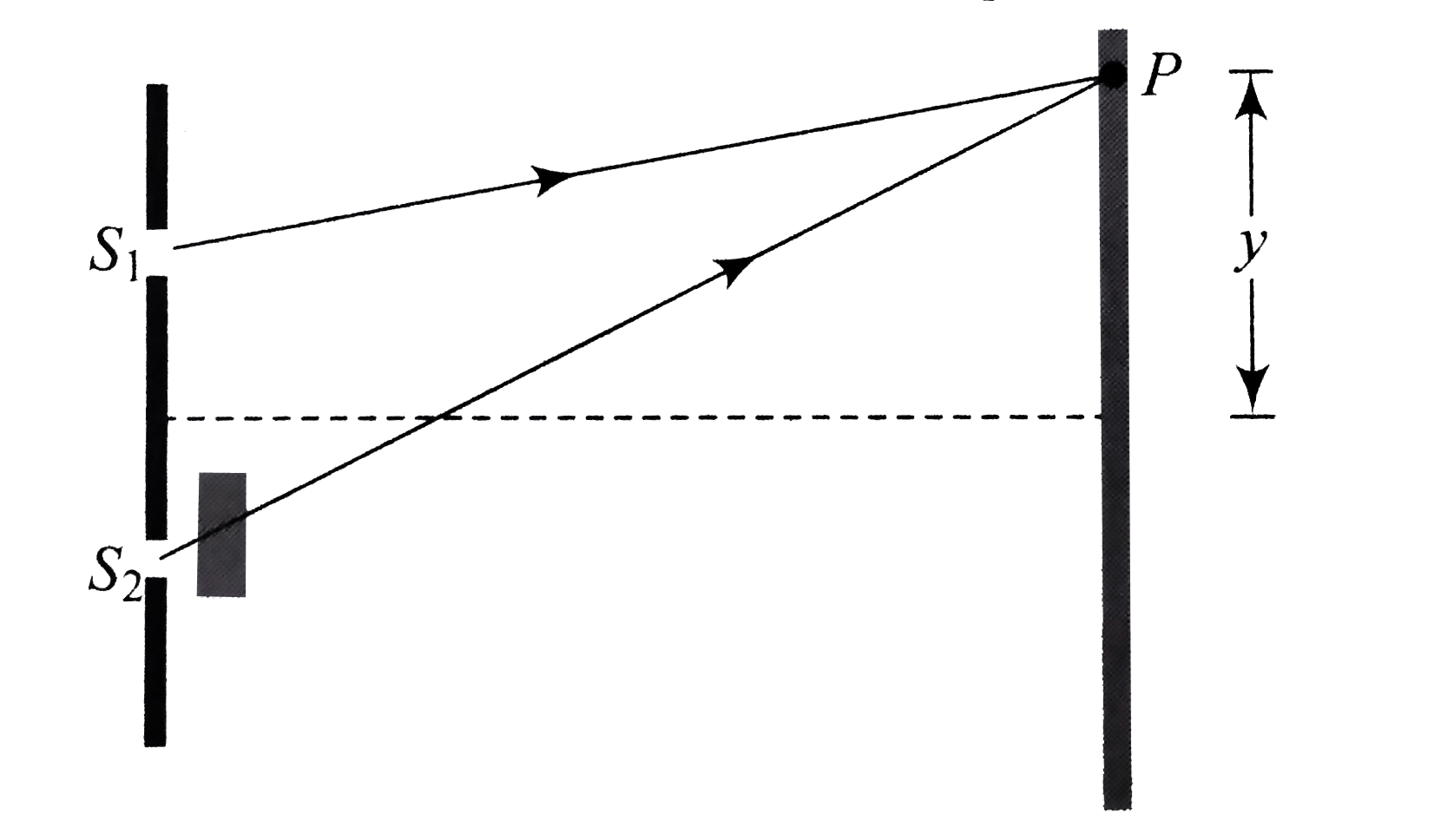
The phase difference at point P without inserting the slab is
View SolutionYoung's double-slit experiment setup with ligth of wavelength λ=6000Å, distance between two slit in 2 mm and distance between the plane of slits and the screen. Is 2 m. The slits are of equal intensity. When a sheet of glass of refractive index 1.5 (which permtis only a fraction η of the incident light to pass through) and thickness 8000Å is placed in front of the lower slit, it is observed that the intensity at a point P, 0.15 mm above the central maxima, does not change.
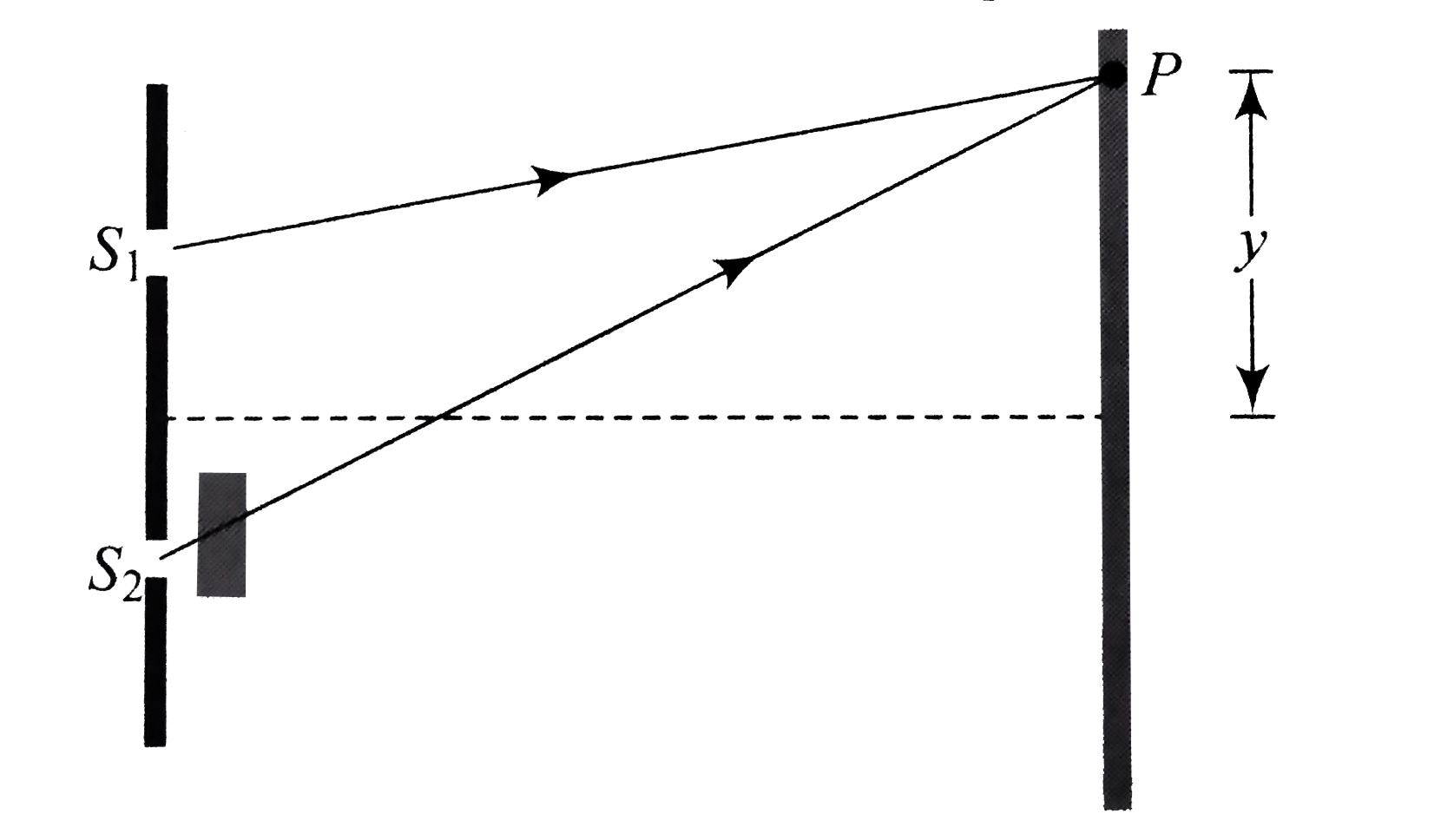
Intensity at point P is
View SolutionYoung's double slit experiment is carried out using microwaves of
wavelength λ=3cm. Distance between the slits is d=5cm and the distance
between the plane of slits and the screen is D=100cm.
(a) Find total number of maxima and
(b) their positions on the screen.
View SolutionYoung's double slit experiment is carried out using microwaves of
wavelength λ=3cm. Distance between the slits is d=5cm and the distance
between the plane of slits and the screen is D=100cm.
(a) Find total number of maxima and
(b) their positions on the screen.
View SolutionIn Young's double slit experiment the light emitted from source has λ=6500Å and the distance between th two slits is 1 mm. Distance between the screen and slit is 1 metre. Distance between third dark and fifth birth fringe will be :
View SolutionThe Young's double slit experiment is carried out with light of wavelength 5000Å. The distance between the slits is 0.2mm and the screen is at 200cm from the slits. The central maximum is at y=0. The third maximum will be at y equal to
View SolutionLight of wavelength λ is incident on a slit of width d and distance between screen and slit is D. Then width of maxima and width of slit will be equal if D is
View SolutionYoung’s double slit experiment is performed with light of wavelength 550 nm . The separation between the slits is 1.10mm and screen is placed at distance of 1 m . What is the distance between the consecutive bright or dark fringes
View SolutionIn Young's double slit experiment, the separation between the slits is halved and the distance between the slits and the screen is doubled. The fringe width is
View SolutionIn Young's double-slit experiment, the separation between the slits is halved and the distance between the slits and the screen in doubled. The fringe width is
View Solution
