If a person has five resistors each of value 1/5 ohm, then the maximum resistance he can obtain by connecting them is
(A) 1 ohm
(B) 5 ohm
(C) 10 ohm
(D) 25 ohm
To find the maximum resistance that can be obtained by connecting five resistors, each with a resistance of 15ohm, we need to connect them in series.
1. Understanding Series Connection:
In a series connection, the total or equivalent resistance Req is the sum of the individual resistances.
2. Identifying the Values:
Each resistor has a resistance of 15ohm. Since there are five resistors, we can denote them as R1,R2,R3,R4,R5.
3. Calculating the Total Resistance:
The formula for total resistance in series is:
Req=R1+R2+R3+R4+R5
Substituting the values:
Req=15+15+15+15+15
4. Simplifying the Expression:
Since there are five resistors, we can factor out 15:
Req=5×15
5. Final Calculation:
Simplifying gives:
Req=1ohm
Thus, the maximum resistance that can be obtained by connecting the five resistors in series is 1 ohm.
Answer:
(A) 1 ohm
In a series connection, the total or equivalent resistance Req is the sum of the individual resistances.
Each resistor has a resistance of 15ohm. Since there are five resistors, we can denote them as R1,R2,R3,R4,R5.
The formula for total resistance in series is:
Req=R1+R2+R3+R4+R5
Substituting the values:
Req=15+15+15+15+15
Since there are five resistors, we can factor out 15:
Req=5×15
Simplifying gives:
Req=1ohm
(A) 1 ohm
Similar Questions
Knowledge Check
A galvanometer has a current sensitivity of 1 mA per division. A variable shunt is connected across the galvanometer and the combination is put in series with a resistance of 500Ω and cell of internal resistance 1Ω. It gives a deflection of 5 division for shunt of 5 ohm and 20 division for shunt of 25 ohm. The emf of cell is
A47.1 VB57.1 VC67.1 VD77.1 V
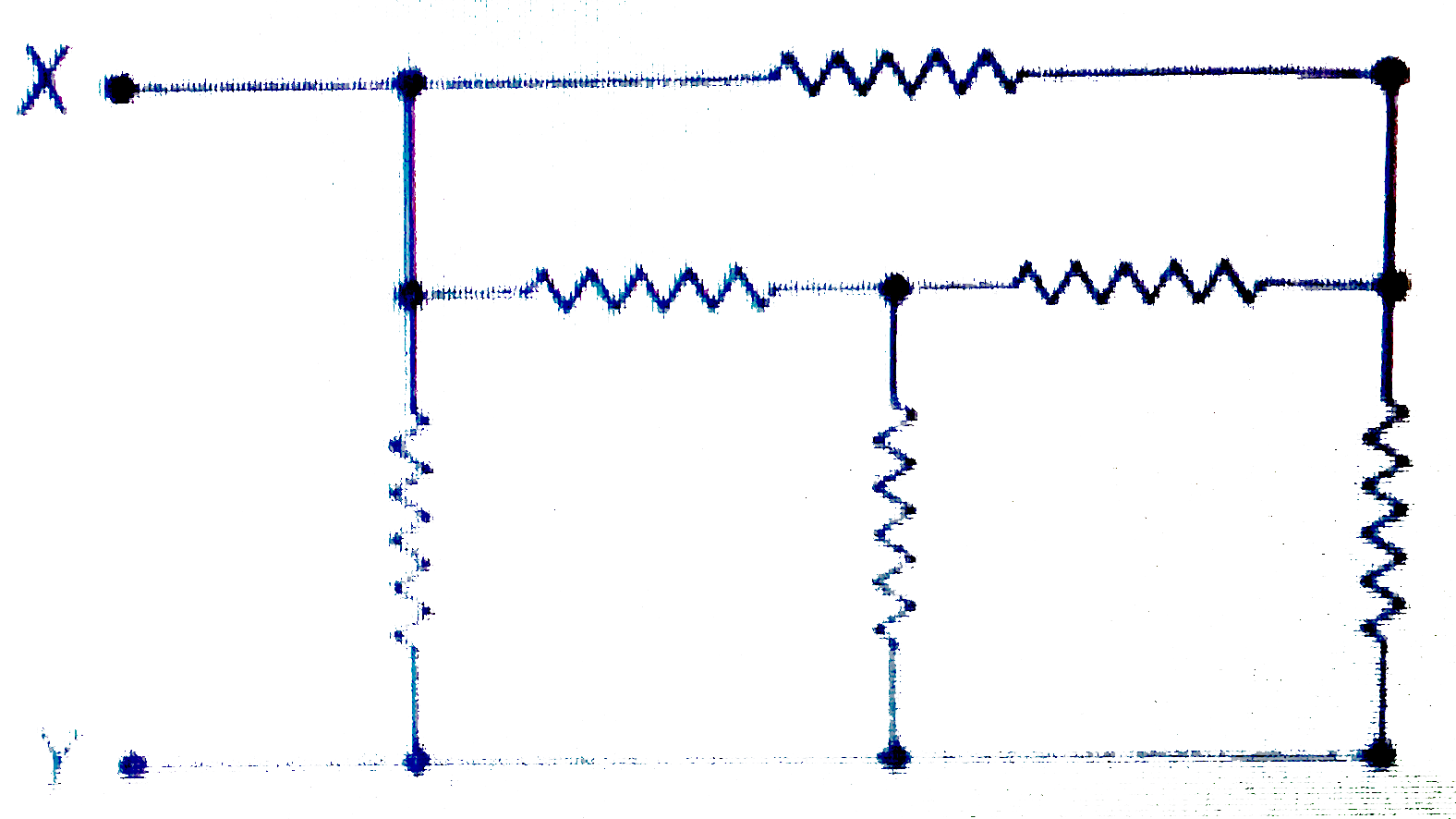
In the adjoining network of resistors, each is of resistance r ohm, the equivalent resistance between points A and B is–

View Solution"The resistance of a wire is 1 ohm". Explain the statement.
View SolutionIn the given circuit all resistances are of value R ohm each. The equivalent resistance between A and Bis :
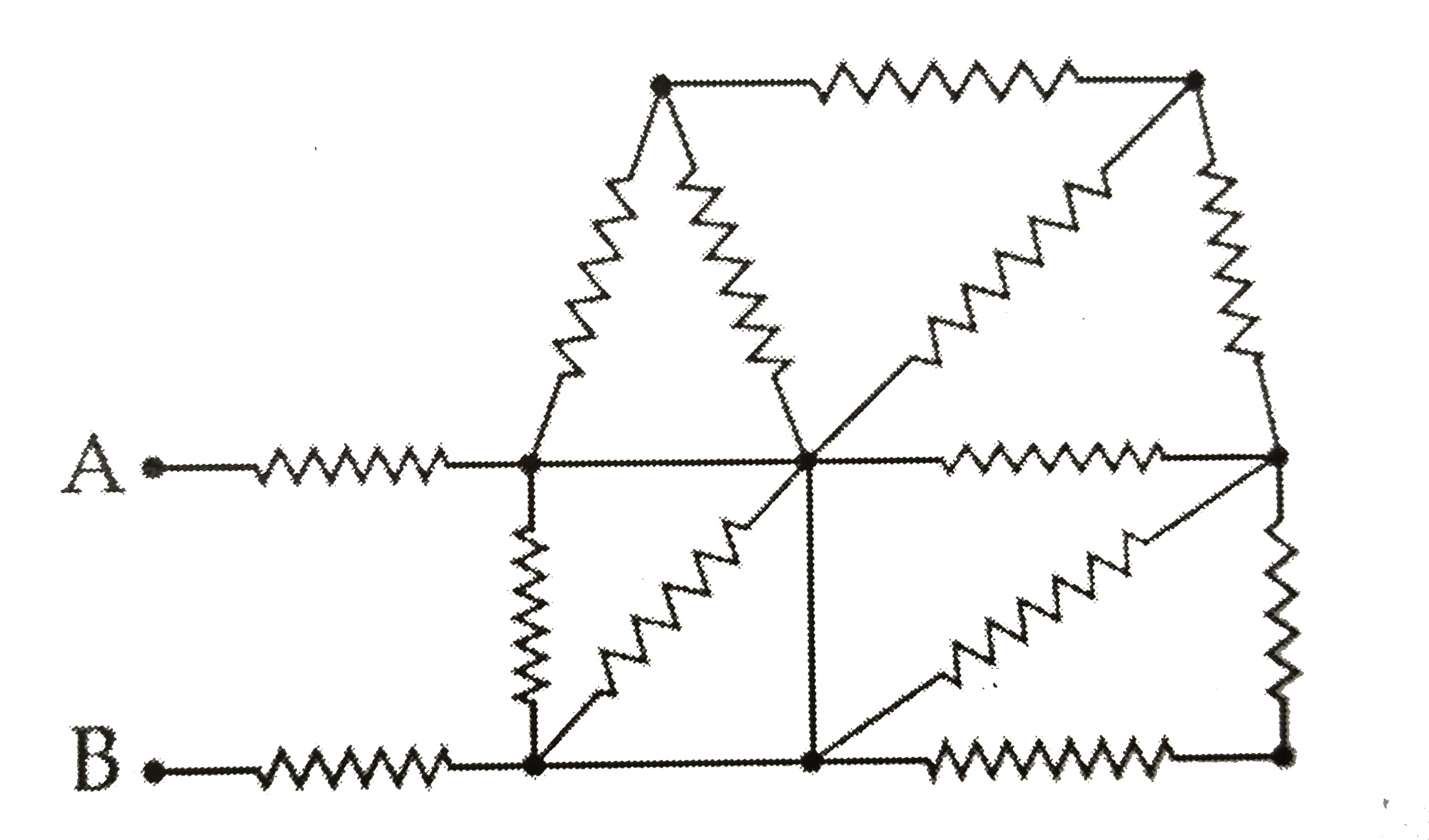
View SolutionAll resistances in fig. 5.34 are in ohm. Find the effective resistance between points A and B.

View SolutionThree resistors each of 2 ohm are connected together in a triangular shape. The resistance between any two vertices will be
View SolutionThe resistance of galvanometer is g ohm and the range is 1 volt. The value of resistance used to convert it into a voltmeter of ragne 10 volt is:-
View SolutionA potentiometer wire of length 10m and resistance 30 ohm is connected in series with a battery of emf 2.5V, internal resistance 5 ohm and external resistance R. If the fall of potential along the potentiometer wire is 50mV/m, the value of R is ohms is
View Solution