Three resistors each of 2 ohm are connected together in a triangular shape. The resistance between any two vertices will be
4/3Ω
3/4Ω
3Ω
6Ω
The correct Answer is:A
To find the equivalent resistance between any two vertices of a triangular arrangement of three resistors, each of 2 ohms, we can follow these steps:
Step 1: Understand the Circuit Configuration
We have three resistors (R1, R2, and R3), each of 2 ohms, connected in a triangular shape. We need to find the equivalent resistance between two vertices, say A and B.
Step 2: Identify the Series and Parallel Connections
From vertex A to vertex B, there are two paths:
1. The path through resistor R1 (2 ohms) and R2 (2 ohms) in series.
2. The path through resistor R3 (2 ohms) directly.
Step 3: Calculate the Resistance in Series
The resistors R1 and R2 are in series. The equivalent resistance (R_eq1) of resistors in series is given by:
Req1=R1+R2=2ohm+2ohm=4ohm
Step 4: Calculate the Equivalent Resistance in Parallel
Now we have two resistances: R_eq1 (4 ohms from the series path) and R3 (2 ohms from the direct path). These two resistances are in parallel. The equivalent resistance (R_eq_total) for resistors in parallel is given by:
1Req_total=1Req1+1R3
Substituting the values:
1Req_total=14+12
Step 5: Simplify the Parallel Resistance
To add these fractions, we find a common denominator (which is 4):
1Req_total=14+24=34
Now, taking the reciprocal to find R_eq_total:
Req_total=43ohm
Step 6: Conclusion
Thus, the equivalent resistance between any two vertices (A and B) of the triangular arrangement of resistors is:
Req_total=43ohm
We have three resistors (R1, R2, and R3), each of 2 ohms, connected in a triangular shape. We need to find the equivalent resistance between two vertices, say A and B.
From vertex A to vertex B, there are two paths:
1. The path through resistor R1 (2 ohms) and R2 (2 ohms) in series.
2. The path through resistor R3 (2 ohms) directly.
The resistors R1 and R2 are in series. The equivalent resistance (R_eq1) of resistors in series is given by:
Req1=R1+R2=2ohm+2ohm=4ohm
Now we have two resistances: R_eq1 (4 ohms from the series path) and R3 (2 ohms from the direct path). These two resistances are in parallel. The equivalent resistance (R_eq_total) for resistors in parallel is given by:
1Req_total=1Req1+1R3
1Req_total=14+12
To add these fractions, we find a common denominator (which is 4):
1Req_total=14+24=34
Req_total=43ohm
Thus, the equivalent resistance between any two vertices (A and B) of the triangular arrangement of resistors is:
Req_total=43ohm
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason
18 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Three resistance each of 4Ω are connected to form a triangle. The resistance between any two terminals is
View SolutionSix resistors each of 10 ohm are connected shown. The equivalent resistance between points X and Y is
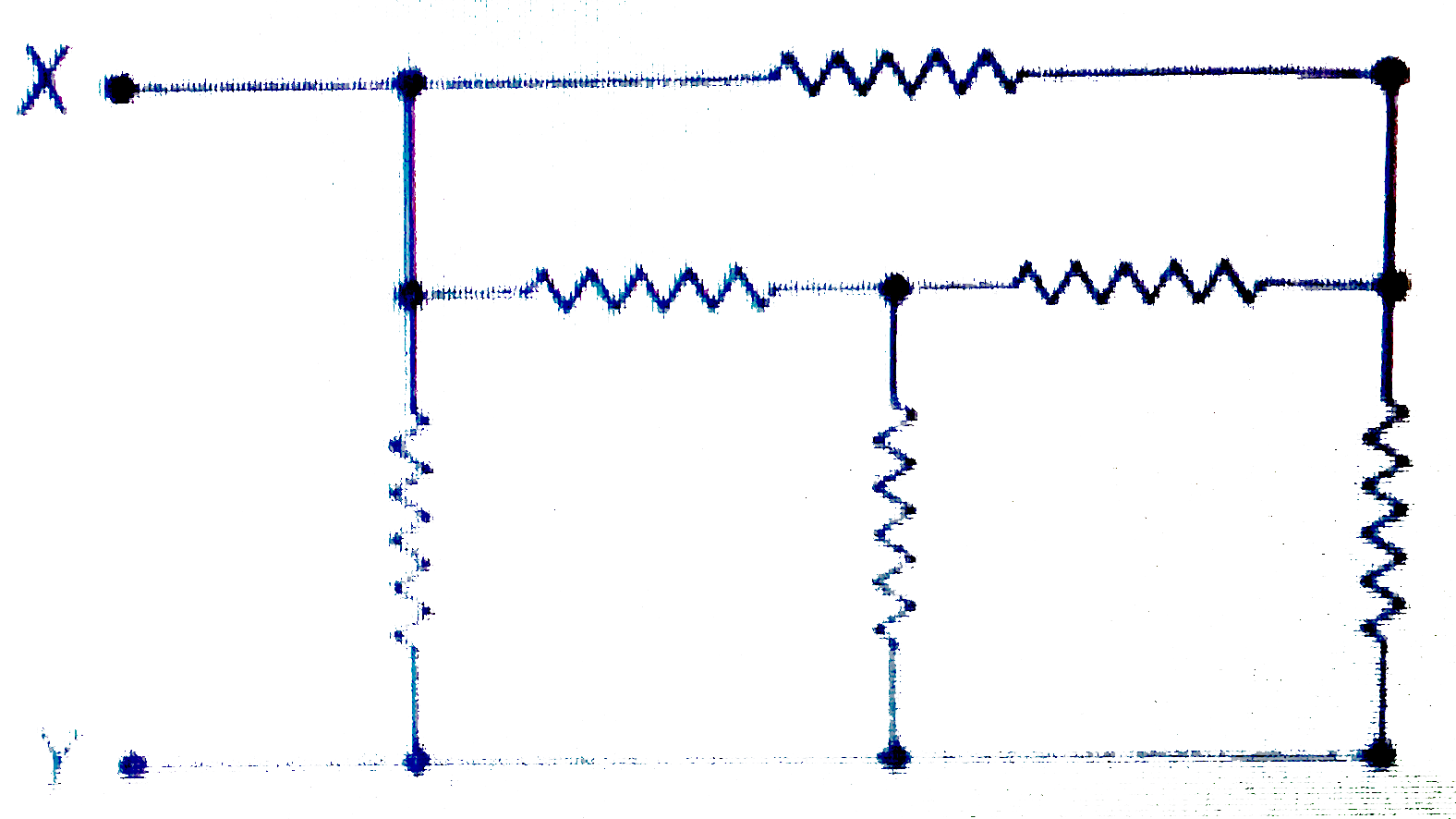
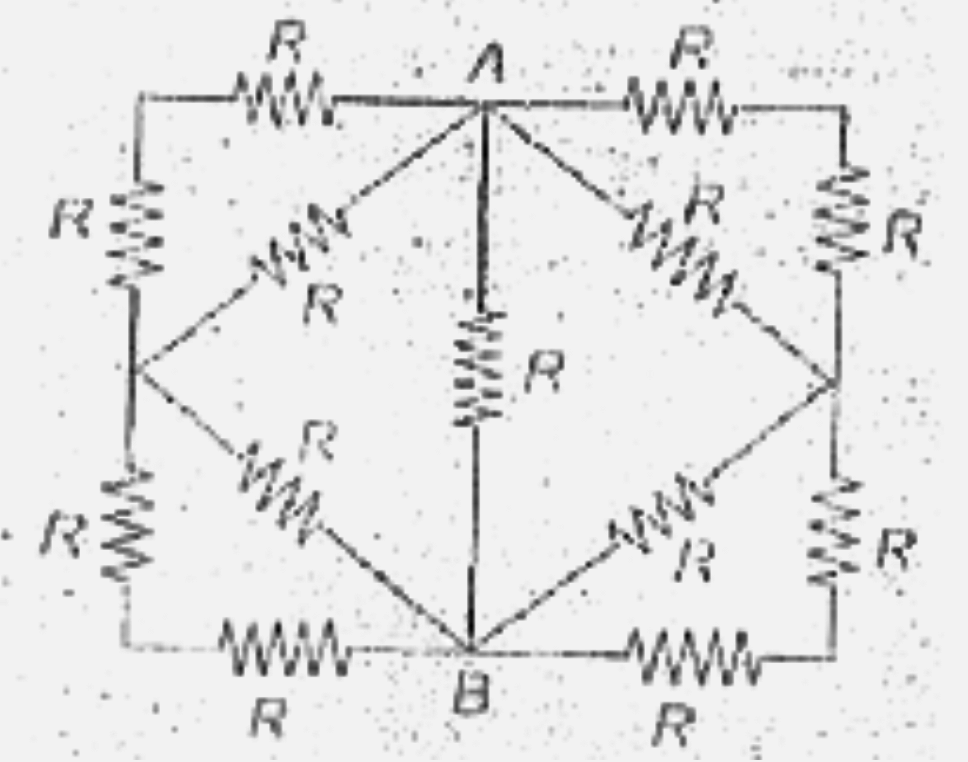
View SolutionThirteen resistors each of resistance R are connected in the circuit as shown . The effective resistance between A and B is
View SolutionThree resistors each of 2 Ω are connected together so that their total resistance is 3 Ω. Draw a diagram to show this arrangement and check it by calculation.
View SolutionNine resistors each of resistance R are connected in the circuit as shown in fig. The net resistance between A and B is

View SolutionA uniform metallic wire has a resistance of 18 Ω and is bent into an equiolateral triangle. Then, the resistance between any two vertices of the triangle is :
View SolutionFive resistors, each of 3 Ω, are connected as shown in Fig . Calculate the resistance
between the points X and Y.

View SolutionFive resistors, each of 3 Ω, are connected as shown in Fig . Calculate the resistance
between the points P and Q,
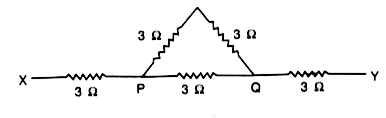
View SolutionSix resistors each of resistance R and two resistors each of resistance r are connected in the network shown below. The equivalent resistance between A and B is
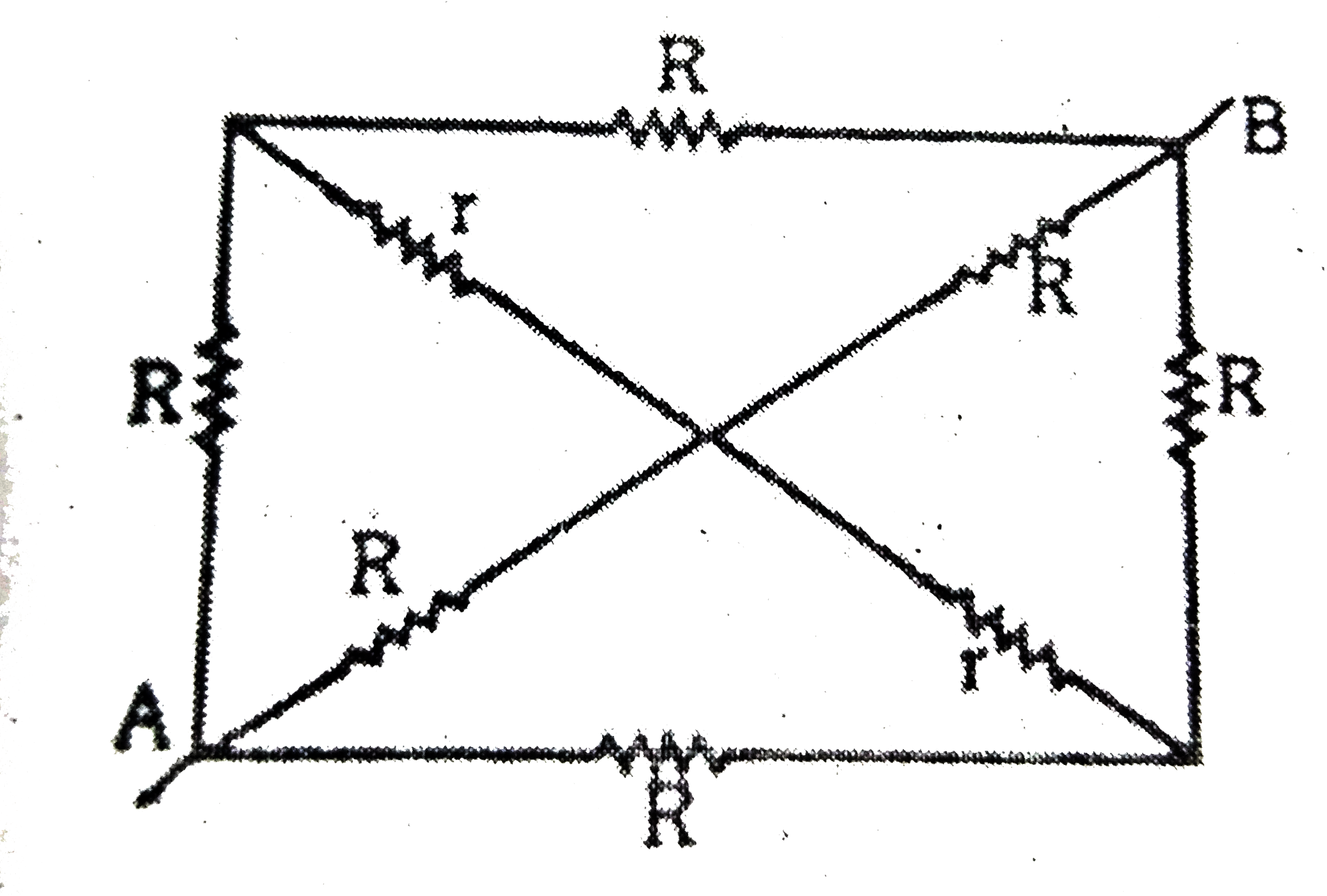
View SolutionTwelve resistors each of resistance 1Ω are connected in the circuit shown in figure. Net resistance between point A and H would be

View Solution
