All squares are
congurent
similar
no similar and no congurent
none of these
The correct Answer is:B
To solve the question "All squares are", we need to analyze the properties of squares and determine the correct relationship among them based on the given options.
1. Understanding Squares:
- A square is a quadrilateral with all four sides equal in length and all angles equal to 90 degrees.
2. Properties of Squares:
- Since all sides of a square are equal, if we have two squares, let’s say square A (with side length 'a') and square B (with side length 'b'), we can express their sides as:
- Square A: AB = a, BC = a, CD = a, DA = a
- Square B: PQ = b, QR = b, RS = b, SP = b
3. Ratio of Sides:
- The ratio of the sides of the squares can be expressed as:
- ABPQ=ab
- BCQR=ab
- CDRS=ab
- DASP=ab
- Since all these ratios are equal, we can conclude that the ratios of the corresponding sides of the squares are constant.
4. Conclusion on Similarity:
- Because the ratios of the corresponding sides of the squares are constant, we can say that the two squares are similar.
- In geometry, two figures are similar if their corresponding angles are equal and the lengths of corresponding sides are proportional.
5. Final Answer:
- Therefore, we conclude that "All squares are similar".
- A square is a quadrilateral with all four sides equal in length and all angles equal to 90 degrees.
- Since all sides of a square are equal, if we have two squares, let’s say square A (with side length 'a') and square B (with side length 'b'), we can express their sides as:
- Square A: AB = a, BC = a, CD = a, DA = a
- Square B: PQ = b, QR = b, RS = b, SP = b
- The ratio of the sides of the squares can be expressed as:
- ABPQ=ab
- BCQR=ab
- CDRS=ab
- DASP=ab
- Since all these ratios are equal, we can conclude that the ratios of the corresponding sides of the squares are constant.
- Because the ratios of the corresponding sides of the squares are constant, we can say that the two squares are similar.
- In geometry, two figures are similar if their corresponding angles are equal and the lengths of corresponding sides are proportional.
- Therefore, we conclude that "All squares are similar".
Topper's Solved these Questions
- CBSE BOARDS 2020BOOK - X BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - CBSE BOARDS 2020EXERCISE - SECTION B
22 Videos
- CBSE BOARDS 2020BOOK - X BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - CBSE BOARDS 2020EXERCISE - SECTION C
33 Videos
- SAMPLE PAPER 2019BOOK - X BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION-C
5 Videos
Similar Questions
Which of the following statements are true and which are false;
All squares are congruent.
If two squares have equal areas, they are congruent.
If two rectangles have equal areas, they are congruent.
If two triangles have equal areas, they are congruent.
View SolutionWrite the component statement of the following statement and check whether the compound statement is true or false
(i) r : All real numbers are complex and all complex numbers are real
(ii) s : All square are rectangle and all rectangle are not square
(iii) t : 2 is a root of equation (x−2)2=0 and 3 is a root of equation x2−3x=0
(iv) Sphere is 3-D solid and square is 2- demensional figure
View Solution
Knowledge Check
In the figure below, all of the small square are equal in area, and the area of rectangle ABCD is 1 square unit. Which of the following expressions represents the area, in square units, of the shaded region?
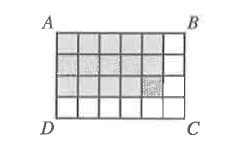 A16⋅14B16⋅34C16⋅56D56⋅34
A16⋅14B16⋅34C16⋅56D56⋅34
If the square of 8×8 chess board are painted either white or black at random then
Statement-1 : The probability that not all squares are in any coloumn, are alternating in colour is (1−127)8.
Statement-3 : The probability that the chess board contains equal number of white and black squares is 64!264.32!.
View SolutionIf three squares are selected at random from chessboard then the probability that all three squares share a common vertex is k find [1k] where denotes greatest integer function
View SolutionA: All square planar complexes can exhibit geometrical isomerism.
R: In square planar complexes metal assumes sp3 hybridisation.
View SolutionIf the mean of 100 observations is 50 and their standard deviations is 5,than the sum of all squares of all the observations is
View SolutionIf the mean of 100 observations is 50 and their standard deviations is 5,than the sum of all squares of all the observations is
View SolutionIf the squares of a 8×8 chess board are painted either red and black at random .The probability that not all squares is any alternating in colour is
View SolutionThe mean of 100 numbers observations is 50 and their standards deviation is 5. The sum of all squares of all the observations is (a)50,000 (b) 250,000 (c) 252500 (d) 255000
View Solution