Which of the following statements are true and which are false;
All squares are congruent.
If two squares have equal
areas, they are congruent.
If two rectangles have
equal areas, they are congruent.
If two triangles have
equal areas, they are congruent.
To determine the truth of the given statements, we will analyze each one step by step.
Step 1: Analyze the statement "All squares are congruent."
- Explanation: Congruent shapes are those that are identical in shape and size. Although all squares have four equal sides and four right angles, they can have different side lengths. For example, a square with a side length of 2 cm is not congruent to a square with a side length of 3 cm.
- Conclusion: This statement is False.
Step 2: Analyze the statement "If two squares have equal areas, they are congruent."
- Explanation: If two squares have equal areas, it means their side lengths must also be equal because the area of a square is calculated as side length squared (Area = side × side). Therefore, if the areas are equal, the side lengths must be equal, making the squares congruent.
- Conclusion: This statement is True.
Step 3: Analyze the statement "If two rectangles have equal areas, they are congruent."
- Explanation: Two rectangles can have the same area but different dimensions. For example, a rectangle with dimensions 2 cm by 4 cm has an area of 8 cm², and a rectangle with dimensions 1 cm by 8 cm also has an area of 8 cm². However, these rectangles are not congruent because their dimensions are different.
- Conclusion: This statement is False.
Step 4: Analyze the statement "If two triangles have equal areas, they are congruent."
- Explanation: Similar to rectangles, two triangles can have the same area but different shapes. For instance, a triangle with a base of 4 cm and height of 2 cm has an area of 4 cm², and another triangle with a base of 8 cm and height of 1 cm also has an area of 4 cm². However, these triangles are not congruent as their dimensions and shapes differ.
- Conclusion: This statement is False.
Final Summary of Statements:
1. All squares are congruent. - False
2. If two squares have equal areas, they are congruent. - True
3. If two rectangles have equal areas, they are congruent. - False
4. If two triangles have equal areas, they are congruent. - False
---
- Explanation: Congruent shapes are those that are identical in shape and size. Although all squares have four equal sides and four right angles, they can have different side lengths. For example, a square with a side length of 2 cm is not congruent to a square with a side length of 3 cm.
- Conclusion: This statement is False.
- Explanation: If two squares have equal areas, it means their side lengths must also be equal because the area of a square is calculated as side length squared (Area = side × side). Therefore, if the areas are equal, the side lengths must be equal, making the squares congruent.
- Conclusion: This statement is True.
- Explanation: Two rectangles can have the same area but different dimensions. For example, a rectangle with dimensions 2 cm by 4 cm has an area of 8 cm², and a rectangle with dimensions 1 cm by 8 cm also has an area of 8 cm². However, these rectangles are not congruent because their dimensions are different.
- Conclusion: This statement is False.
- Explanation: Similar to rectangles, two triangles can have the same area but different shapes. For instance, a triangle with a base of 4 cm and height of 2 cm has an area of 4 cm², and another triangle with a base of 8 cm and height of 1 cm also has an area of 4 cm². However, these triangles are not congruent as their dimensions and shapes differ.
- Conclusion: This statement is False.
1. All squares are congruent. - False
2. If two squares have equal areas, they are congruent. - True
3. If two rectangles have equal areas, they are congruent. - False
4. If two triangles have equal areas, they are congruent. - False
Topper's Solved these Questions
Similar Questions
If the areas of two similar triangles are equal, prove that they are congruent.
View SolutionIf the areas of two similar triangles are equal, prove that they are congruent.
View SolutionState which of the following statements are true and which are false :
A triangle can have two right angles.
View SolutionProve that a median divides a triangle into two triangles of equal area.
View SolutionFill in the blanks: Two square are congruent if
Two rectangles are congruent if
Two circles are congruent if
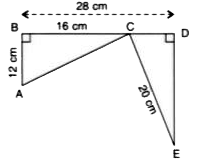
View SolutionShow that the two triangles given the following figure are congruent.
View SolutionWhich of the following statements are true (T) and which are false (F): Side opposite to equal angles of a triangle may be unequal. Angle opposite to equal sides of a triangle are equal. The measure of each angle of an equilateral triangle is 600 If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles. The bisectors of two equal angles of a triangle are equal. If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles. The two altitudes corresponding to two equal sides of a triangle need not be equal. If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent. Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal to the hypotenuse and a side of the other triangle.
View SolutionIf two angles and a side of one triangles are equal to two angles and a side of another triangles , the triangles are congruent.
View SolutionWhich of the following pairs of triangle are congruent by ASA condition?
View SolutionShow that a median of a triangle divides it into two triangles of equal areas.
View Solution
