Match the statements/expressions in Column I with the statements/expression in Column II. Column I Column II Root(s) of the equation 2sin2θ+sin22θ=2 (p) π6 Points of discontinuity of the function f(x)=[6xπ]cos[3xπ], where [y] denotes the largest integer less than or equal to y (q) π3 Volume of the parallelepiped with its edges represented by the vectors →a,→band→c are unit vectors satisfying →a+→b+√3→c=→0 (r) π2
To solve the problem, we need to match the statements in Column I with the corresponding expressions in Column II. We will analyze each statement one by one.
Step 1: Find the roots of the equation 2sin2θ+sin22θ=2
1. We start with the equation:
2sin2θ+sin22θ=2
2. We know that sin22θ=4sin2θcos2θ. Substituting this into the equation gives:
2sin2θ+4sin2θcos2θ=2
3. Rearranging the equation:
2sin2θ+4sin2θ(1−sin2θ)=2
4. This simplifies to:
2sin2θ+4sin2θ−4sin4θ=2
4sin4θ−6sin2θ+2=0
5. Let x=sin2θ. The equation becomes:
4x2−6x+2=0
6. Using the quadratic formula x=−b±√b2−4ac2a:
x=6±√(−6)2−4⋅4⋅22⋅4
x=6±√36−328
x=6±28
x=1orx=12
7. Therefore, sin2θ=1 or sin2θ=12. This gives:
θ=π2orθ=π4
Step 2: Find the points of discontinuity of the function f(x)=(6xπ)cos(3xπ)
1. The function f(x) is discontinuous at points where (6xπ) changes its value.
2. The expression 6xπ will change its integer part at:
6xπ=nfor integers n
x=nπ6
3. The values of n that yield x in the range of interest (0 to π) are n=0,1,2,3,4,5,6, giving:
x=0,π6,π3,π2,5π6,π
4. Thus, the points of discontinuity are:
x=π6,π3,π2,π
Step 3: Find the volume of the parallelepiped with edges represented by the vectors →a,→b,→c
1. The volume V of the parallelepiped formed by the vectors →a,→b,→c is given by the scalar triple product:
V=|→a⋅(→b×→c)|
2. Given that →a+→b+√3→c=→0, we can express →c as:
→c=−1√3(→a+→b)
3. Assuming →a,→b,→c are unit vectors, we can calculate the volume. However, without loss of generality, if we assume they are orthogonal, the volume can be simplified to:
V=1(since the vectors are unit vectors)
Final Matching
- The roots of the equation 2sin2θ+sin22θ=2 correspond to π4 and π2.
- The points of discontinuity of f(x) correspond to π6, π3, and π2.
- The volume of the parallelepiped corresponds to the unit vectors.
Thus, the final matching is:
- (p) π6 matches with the points of discontinuity.
- (q) π3 matches with the points of discontinuity.
- (r) π2 matches with the roots of the equation.
2sin2θ+sin22θ=2
2. We know that sin22θ=4sin2θcos2θ. Substituting this into the equation gives:
2sin2θ+4sin2θcos2θ=2
3. Rearranging the equation:
2sin2θ+4sin2θ(1−sin2θ)=2
4. This simplifies to:
2sin2θ+4sin2θ−4sin4θ=2
4sin4θ−6sin2θ+2=0
5. Let x=sin2θ. The equation becomes:
4x2−6x+2=0
6. Using the quadratic formula x=−b±√b2−4ac2a:
x=6±√(−6)2−4⋅4⋅22⋅4
x=6±√36−328
x=6±28
x=1orx=12
7. Therefore, sin2θ=1 or sin2θ=12. This gives:
θ=π2orθ=π4
2. The expression 6xπ will change its integer part at:
6xπ=nfor integers n
x=nπ6
3. The values of n that yield x in the range of interest (0 to π) are n=0,1,2,3,4,5,6, giving:
x=0,π6,π3,π2,5π6,π
4. Thus, the points of discontinuity are:
x=π6,π3,π2,π
V=|→a⋅(→b×→c)|
2. Given that →a+→b+√3→c=→0, we can express →c as:
→c=−1√3(→a+→b)
3. Assuming →a,→b,→c are unit vectors, we can calculate the volume. However, without loss of generality, if we assume they are orthogonal, the volume can be simplified to:
V=1(since the vectors are unit vectors)
- The points of discontinuity of f(x) correspond to π6, π3, and π2.
- The volume of the parallelepiped corresponds to the unit vectors.
- (p) π6 matches with the points of discontinuity.
- (q) π3 matches with the points of discontinuity.
- (r) π2 matches with the roots of the equation.
Topper's Solved these Questions
Similar Questions
Match the conditions/ expressions in Column I with statement in Column II
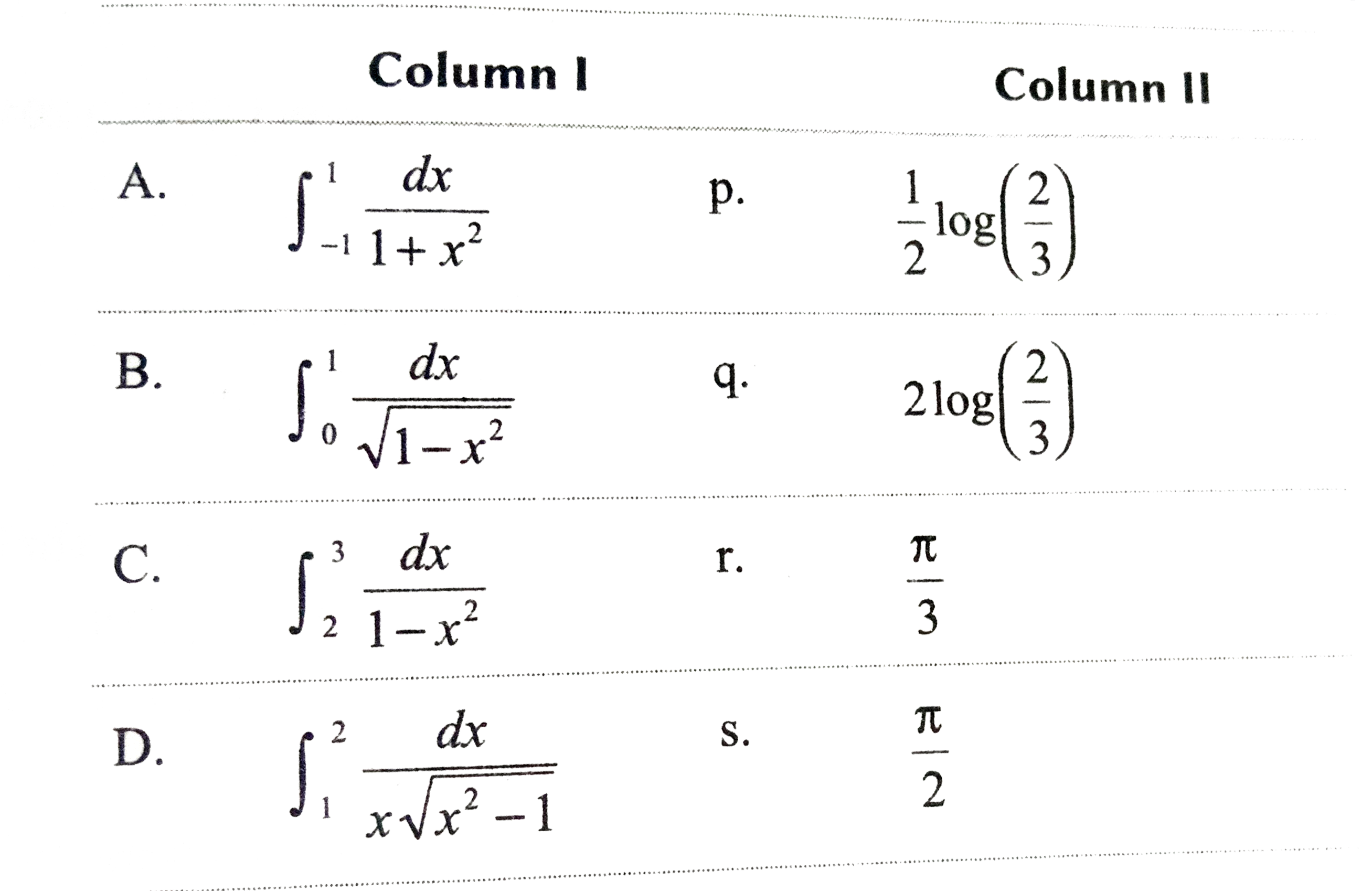
View SolutionMatch the conditions / expression in Column I with statement in Column II.
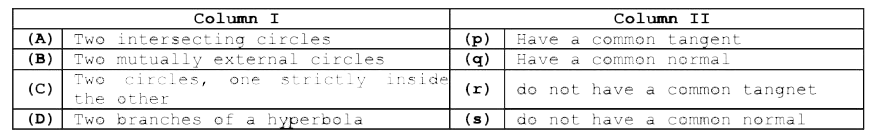
View SolutionThe function f(x)=tan|π[x−π]|1+[x]2, where [x] denotes the greatest integer less than or equal to x, is
View SolutionThe function f(x)=3sin2π+sin4πx+x−[x] where [x] denotes the greatest interger less than or equal to x, is
View SolutionThe function f(x)=[x]cos(2x−12)π where [ ] denotes the greatest integer function, is discontinuous
View SolutionThe points of discontinuities of f(x)=[6xπ]cos[3xπ]in[π6,π] is/are:(where [.] denotes greattest integer function)
View SolutionIf f(x)=sin[π2]x+sin[−π2]x, where [x] denotes the greatest integer less than or equal to
A. f(π/2)=1
B. f(π)=2
C. f(π/4)=−1
D. none of these
View SolutionIf f(x)=cos[π]x+cos[πx], where [y] is the greatest integer function of y then f(π2) is equal to
View SolutionThe period of the function
f(x)=cos2π{2x}−sin2π{2x},
is ( where {x} denotes the functional part of x)
View SolutionIf f(x)=sin{π3[x]−x2} for 2<x<3 and [x] denotes the greatest integer less than or equal to x, then f'(√π/3) is equal to
View Solution
