If , , then (a) exists for (b) exists for (c) does not exist for any value of (d) cannot be determined
To solve the problem, we need to analyze the limit of the function f(x) as x approaches 0. The function is defined as follows:
f(x)={xnsin(1x2)if x≠00if x=0
We need to evaluate the limit limx→0f(x) for different values of n.
Step 1: Evaluate the Right-Hand Limit
We start by evaluating the right-hand limit:
limx→0+f(x)=limx→0+xnsin(1x2)
As x→0+, xn approaches 0 if n>0. The sine function, sin(1x2), oscillates between -1 and 1, so it is bounded. Therefore, we can conclude:
limx→0+f(x)=0⋅(bounded)=0
Step 2: Evaluate the Left-Hand Limit
Next, we evaluate the left-hand limit:
limx→0−f(x)=limx→0−xnsin(1x2)
Similar to the right-hand limit, as x→0−, xn approaches 0 if n>0. The sine function remains bounded. Thus, we have:
limx→0−f(x)=0⋅(bounded)=0
Step 3: Conclusion for n≥1
Since both the right-hand limit and the left-hand limit equal 0, we conclude that:
limx→0f(x)=0for n≥1
Step 4: Consider n<0
If n<0, as x→0, xn approaches infinity. The sine function still oscillates between -1 and 1. Therefore, the limit does not exist because f(x) does not approach a finite value.
Final Conclusion
- For n>1: The limit exists and equals 0.
- For n<0: The limit does not exist.
- For n=1: The limit exists and equals 0.
Answer Selection
Based on the analysis:
- (a) True: limx→0f(x) exists for n≥1.
- (b) False: limx→0f(x) does not exist for n<0.
- (c) False: limx→0f(x) exists for n≥1.
- (d) False: The limit can be determined.
Thus, the correct option is (a).
- For n<0: The limit does not exist.
- For n=1: The limit exists and equals 0.
- (b) False: limx→0f(x) does not exist for n<0.
- (c) False: limx→0f(x) exists for n≥1.
- (d) False: The limit can be determined.
Topper's Solved these Questions
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Book:CENGAGE ENGLISHChapter:DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Exercise:Multiple correct answers type
Explore 11 Videos
- LINEAR INEQUALITIESBook:CENGAGE ENGLISHChapter:LINEAR INEQUALITIESExercise:All Questions
Explore 68 Videos
Similar Questions
limx→0xsecx
View Solutionlimx→0(x3logx)
View Solutionlimx→0sinxx=?
View Solutionlimx→0(x2−3x+2)
View SolutionIf f(x)={xsin(1x)x≠00x=0 Then, limx→0f(x)
View SolutionEvaluate limx→0f(x), where
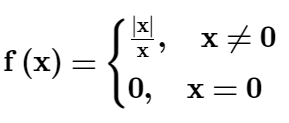
View SolutionEvaluate: limx→0xx
View Solutionlimx→0x2−xsinx
View Solutionlimx→0(1−cosxx2)
View SolutionIf f(x)=|x|x, then show that limx→0f(x) does not exist.
View Solution