If f(x)={xsin(1x)x≠00x=0 Then, limx→0f(x)
is equal to 1
is equal to−1
is equal to 0
does not exist
The correct Answer is:C
To find the limit of the function f(x) as x approaches 0, we start with the definition of the function:
f(x)={xsin(1x)if x≠00if x=0
We need to evaluate:
limx→0f(x)
Step 1: Analyze the limit for x≠0
Since we are interested in the limit as x approaches 0, we will focus on the case when x≠0:
limx→0f(x)=limx→0xsin(1x)
Step 2: Evaluate the behavior of sin(1x)
The function sin(1x) oscillates between -1 and 1 as x approaches 0. Therefore, we can say:
−1≤sin(1x)≤1
Step 3: Multiply by x
Now, if we multiply the entire inequality by x (keeping in mind that x approaches 0), we have:
−x≤xsin(1x)≤x
Step 4: Apply the Squeeze Theorem
As x approaches 0, both −x and x approach 0. Therefore, by the Squeeze Theorem:
limx→0xsin(1x)=0
Step 5: Conclude the limit
Thus, we conclude:
limx→0f(x)=0
Final Answer
The limit is:
limx→0f(x)=0
Topper's Solved these Questions
- LIMITSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - LIMITSEXERCISE - Chapter Test
58 Videos
- LIMITSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - LIMITSEXERCISE - Section II - Assertion Reason Type
5 Videos
- INVERSE TRIGONOMETRIC FUNCTIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONS EXERCISE - Chapter Test
30 Videos
- MATHEMATICAL INDUCTION BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise
30 Videos
Similar Questions
limx→0xsecx
View Solutionlimx→0sinxx=?
View SolutionIf f(x)={x−|x|x,x≠02, x=0,show that limx→0f(x) does not exist.
View SolutionIf f(x)={xnsin(1x2)x≠00x=0, (n∈I), then (a) limx→0f(x) exists for n>1 (b) limx→0f(x) exists for n<0 (c) limx→0f(x) does not exist for any value of n (d) limx→0f(x) cannot be determined
View SolutionIf f(x) is defined as follows:
f(x)=⎧⎪⎨⎪⎩1x>0−1x<00x=0
Then show that limx→0f(x) does not exist.
View SolutionEvaluate limx→0f(x), where
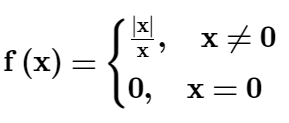
View Solutionlimx→0(x3logx)
View Solutionf(x)={x2x2+|x|x≠01x=0then f(x) is
View SolutionIf f(x) is defined as
f(x)={2x+3x≤03x+3x≥0
then evaluate : limx→0f(x)andlimx→1f(x)
View SolutionIf f(x)={x−|x|x,x≠0,2,x=0, show that limx→0 f(x) does not exist.
View Solution
