In how many points graph of y=x3−3x2+5x−3 intersect the x-axis?
To determine how many points the graph of the function y=x3−3x2+5x−3 intersects the x-axis, we need to find the values of x for which y=0. This means we need to solve the equation:
x3−3x2+5x−3=0
Step 1: Finding a root
Let's start by checking if x=1 is a root of the equation:
y=13−3(12)+5(1)−3
=1−3+5−3
=0
Since y=0 when x=1, we can conclude that x=1 is indeed a root of the equation.
Step 2: Factor the polynomial
Since x=1 is a root, we can factor the polynomial as follows:
x3−3x2+5x−3=(x−1)(Ax2+Bx+C)
To find A, B, and C, we can perform polynomial long division or synthetic division of x3−3x2+5x−3 by x−1.
Performing synthetic division:
11−35−31−231−230
The result of the division is:
x2−2x+3
So we can write:
x3−3x2+5x−3=(x−1)(x2−2x+3)
Step 3: Finding the roots of the quadratic
Next, we need to find the roots of the quadratic x2−2x+3 using the discriminant:
D=b2−4ac=(−2)2−4(1)(3)=4−12=−8
Since the discriminant D<0, the quadratic x2−2x+3 has no real roots.
Conclusion
Thus, the only real root of the original polynomial x3−3x2+5x−3 is x=1. Therefore, the graph of the function intersects the x-axis at exactly one point.
Final Answer
The graph of y=x3−3x2+5x−3 intersects the x-axis at 1 point.
---
=1−3+5−3
=0
Topper's Solved these Questions
Similar Questions
Knowledge Check
In how many different points does the graph of the function f(x)=x3−2x2+x−2 intersect the x-axis?
A0B1C2D3What is the y - coordinate of the point at which the graph of y = 2 sin x - cos 2 x intersects the y - axis ?
A−2B−1C0D1The graphs of y=2x-5 and x + 3y=-1 intersect at
A(-1,2)B(-2,-1)C(2,-1)D(-2,1)
In how many points the graph of f(x)=x3+2x2+3x+4 meets the x-axis ?
View SolutionIn how many points the graph of f(x)=x3+2x2+3x+4 meets the xaξs ?
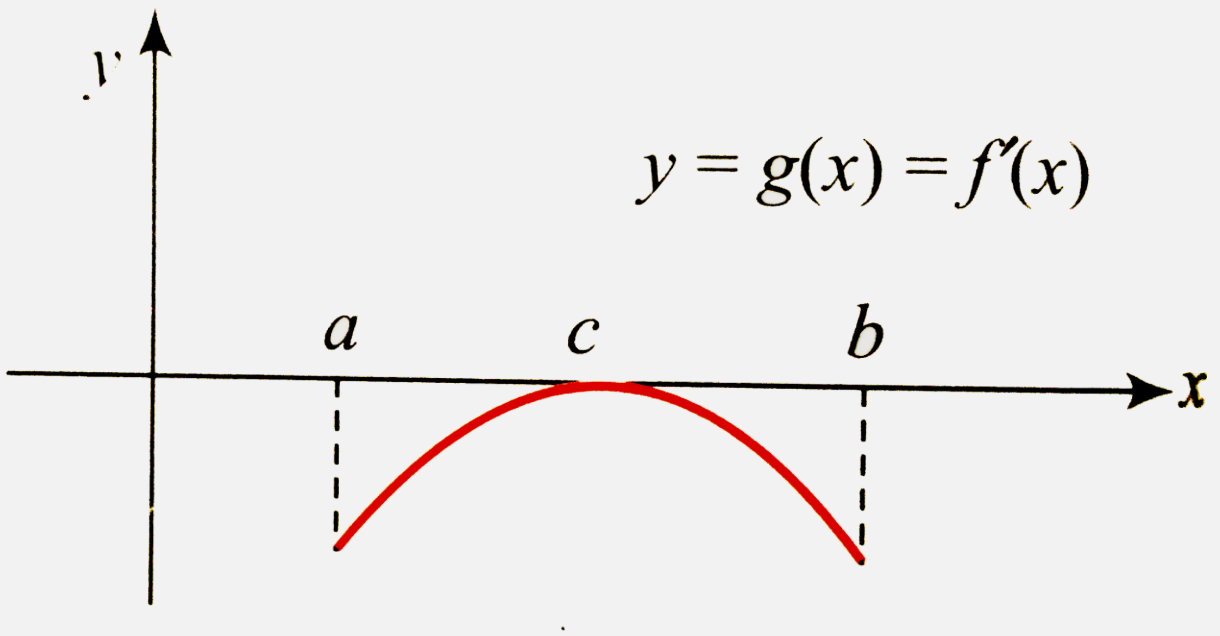
View SolutionFollowing is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, a≤x≤b.
(c) How many points of inflection the graph of y=f(x),a≤x≤b, has?
(d) Find the points of local maxima/minima ofy=f(x),a<xb.
(e) How many roots equation f''(x)=0 has?
View SolutionIn the xy-plane, the graph of y=3x2−14x intersects the graph of y = x at the points (0, 0) and (a, a). What is the value of a ?
View SolutionAnalyze the graph of y=3x2+2x+5
View Solution
