In how many points the graph of f(x)=x3+2x2+3x+4 meets the x-axis ?
To determine how many points the graph of the function f(x)=x3+2x2+3x+4 meets the x-axis, we need to find the roots of the equation f(x)=0. Here’s a step-by-step solution:
Step 1: Set the function equal to zero
We start by setting the function equal to zero:
x3+2x2+3x+4=0
Step 2: Analyze the behavior of the function as x approaches infinity and negative infinity
- As x→+∞:
The leading term x3 dominates, so f(x)→+∞.
- As x→−∞:
Again, the leading term x3 dominates, so f(x)→−∞.
Step 3: Find the derivative of the function
To understand the nature of the function, we find the derivative:
f′(x)=3x2+4x+3
Step 4: Determine the nature of the derivative
Next, we calculate the discriminant of the quadratic f′(x):
D=b2−4ac=42−4⋅3⋅3=16−36=−20
Since the discriminant is less than zero, this means that f′(x) does not have real roots and is always positive (as the coefficient of x2 is positive).
Step 5: Conclusion on the function's behavior
Since f′(x)>0 for all x, the function f(x) is always increasing.
Step 6: Analyze the function's values
Given that f(x) goes from −∞ to +∞ and is always increasing, it must cross the x-axis exactly once.
Final Answer
Thus, the graph of f(x)=x3+2x2+3x+4 meets the x-axis at exactly one point.
---
We start by setting the function equal to zero:
x3+2x2+3x+4=0
- As x→+∞:
The leading term x3 dominates, so f(x)→+∞.
- As x→−∞:
Again, the leading term x3 dominates, so f(x)→−∞.
To understand the nature of the function, we find the derivative:
f′(x)=3x2+4x+3
Next, we calculate the discriminant of the quadratic f′(x):
D=b2−4ac=42−4⋅3⋅3=16−36=−20
Since the discriminant is less than zero, this means that f′(x) does not have real roots and is always positive (as the coefficient of x2 is positive).
Since f′(x)>0 for all x, the function f(x) is always increasing.
Given that f(x) goes from −∞ to +∞ and is always increasing, it must cross the x-axis exactly once.
Thus, the graph of f(x)=x3+2x2+3x+4 meets the x-axis at exactly one point.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In how many different points does the graph of the function f(x)=x3−2x2+x−2 intersect the x-axis?
A0B1C2D3
In how many points graph of y=x3−3x2+5x−3 interest the x-axis?
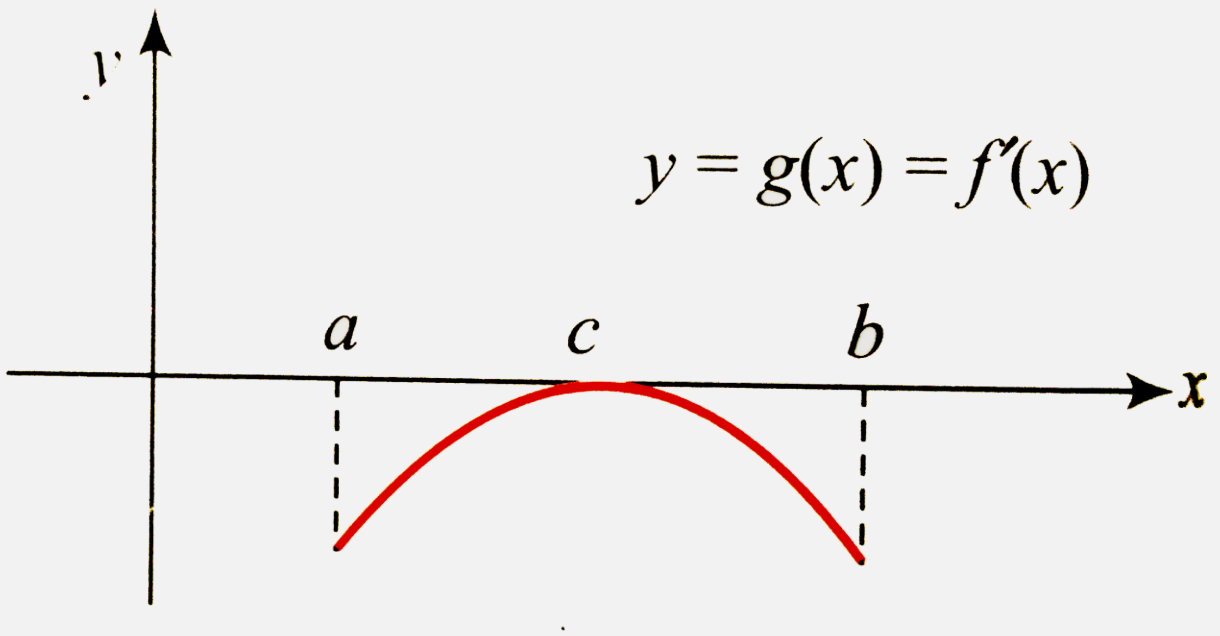
View SolutionFollowing is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, a≤x≤b.
(c) How many points of inflection the graph of y=f(x),a≤x≤b, has?
(d) Find the points of local maxima/minima ofy=f(x),a<xb.
(e) How many roots equation f''(x)=0 has?
View SolutionDraw and discuss the graph of f(x)=x2/3−x4/3
View SolutionHow many x-intercepts does f(x)=x2+3x+3 have?
View SolutionDraw the graph of f(x)=5x2(x−1)3.
View SolutionDraw the graph of f(x)=x3−xx2−1.
View SolutionDraw the graph of f(x)=(x−1)|(x−2)(x−3)|.
View Solution