There are 2 women participating in a chess tournament. Every participant played 2 games with the other participants. The number of games that the men played between themselves exceeded by 66 as compared to the number of games that the men played with women. If the number of participants is n , then the value of n−6 is ______.
To solve the problem step by step, we will define the variables and set up equations based on the information given in the question.
Step 1: Define Variables
Let the number of men participating in the chess tournament be m. Since there are 2 women, the total number of participants n can be expressed as:
n=m+2
Step 2: Calculate Games Played Between Men
Each participant plays 2 games with every other participant. The number of games played between men can be calculated using combinations. The number of ways to choose 2 men from m men is given by (m2). Since each pair of men plays 2 games, the total number of games played between men is:
Games between men=2×(m2)=2×m(m−1)2=m(m−1)
Step 3: Calculate Games Played Between Men and Women
Each man plays 2 games with each woman. Since there are 2 women, the total number of games played between men and women is:
Games between men and women=2×m×2=4m
Step 4: Set Up the Equation
According to the problem, the number of games played between men exceeds the number of games played between men and women by 66. Therefore, we can set up the equation:
m(m−1)=4m+66
Step 5: Rearrange the Equation
Rearranging the equation gives us:
m2−m−4m−66=0
m2−5m−66=0
Step 6: Factor the Quadratic Equation
We can factor the quadratic equation:
(m−11)(m+6)=0
Step 7: Solve for m
Setting each factor to zero gives us:
1. m−11=0 → m=11
2. m+6=0 → m=−6 (not valid since m cannot be negative)
Thus, we have:
m=11
Step 8: Calculate Total Number of Participants n
Now, substituting m back into the equation for n:
n=m+2=11+2=13
Step 9: Find n−6
Finally, we need to find n−6:
n−6=13−6=7
Final Answer
The value of n−6 is:
7
Let the number of men participating in the chess tournament be m. Since there are 2 women, the total number of participants n can be expressed as:
n=m+2
Each participant plays 2 games with every other participant. The number of games played between men can be calculated using combinations. The number of ways to choose 2 men from m men is given by (m2). Since each pair of men plays 2 games, the total number of games played between men is:
Games between men=2×(m2)=2×m(m−1)2=m(m−1)
Each man plays 2 games with each woman. Since there are 2 women, the total number of games played between men and women is:
Games between men and women=2×m×2=4m
According to the problem, the number of games played between men exceeds the number of games played between men and women by 66. Therefore, we can set up the equation:
m(m−1)=4m+66
Rearranging the equation gives us:
m2−m−4m−66=0
m2−5m−66=0
We can factor the quadratic equation:
(m−11)(m+6)=0
Setting each factor to zero gives us:
1. m−11=0 → m=11
2. m+6=0 → m=−6 (not valid since m cannot be negative)
m=11
Now, substituting m back into the equation for n:
n=m+2=11+2=13
Finally, we need to find n−6:
n−6=13−6=7
The value of n−6 is:
7
Topper's Solved these Questions
Similar Questions
There were two women participating in a chess tournament. Every participant played two games with the other participants. The number of games that the men played among themselves proved to exceed by 66 number of games that the men played with the women. The number of participants is a. 6 b. 11 c. 13 d. none of these
View SolutionTwo women and some men participated in a chess tournament in which every participant played two games with each of the other participants. If the number of games that the men played between themselves exceeds the number of games that the men played with the women by 66, then the number of men who participated in the tournament lies in the interval
View Solution
Knowledge Check
At the end of the season, the ratio of the number of games team has won to the number of games it lost it 4:3. If the team won 12 games and each game played ended in either a win or lose, how many games did the team play during season?
A9B15C18D21
There are m men and two women participating in a chess tournament. Each participant plays two games with every other participant. If the number of games played by the men between themselves exceeds the number of games played between the men and the women by 84, then teh value of m is
View SolutionIn a badminton each player played one game with ll the other players. Number of players participated in the tournament if they played 105 games is
View SolutionIf in a chess tournament each contestant plays once against each of the other and in all 45 games are played, then the number of participants, is
View SolutionIn a class tournament where the participants were to play one game with one another, two of the class players fell ill, having played 3 games each. If the total number of games played is 24, then the number of participants at the beginning was
View SolutionIn a class tournament, all participants were to plan different game with one another. Two players fell ill after having played three games each. If the total number of games played in the tournament is equal to 84, the total number of participants in the beginning was equal to a. 10 b. 15 c. 12 d. 14
View Solution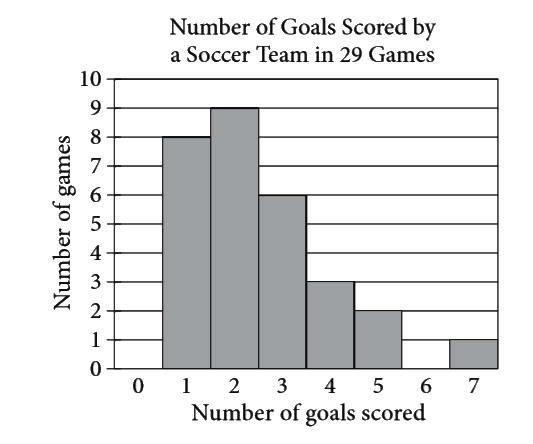
Based on the graph above, in how many of the games played did the soccer team score goals equal to the median number of goals for the 29 games?
View SolutionIn a football championship, 153 matches were played. Every two teams played one match with each other. The number of teams, participating in the championship is …….. .
View Solution
