If in a chess tournament each contestant plays once against each of the other and in all 45 games are played, then the number of participants, is
9
10
15
none of these
The correct Answer is:B
To solve the problem, we need to determine the number of participants in a chess tournament where each contestant plays once against each other, and a total of 45 games are played.
1. Understanding the Problem:
Each contestant plays against every other contestant exactly once. If there are n contestants, the number of games played can be represented by the combination formula (n2), which gives the number of ways to choose 2 contestants from n.
2. Setting Up the Equation:
We know that the total number of games played is 45. Therefore, we can set up the equation:
(n2)=45
This can be expanded to:
n(n−1)2=45
3. Eliminating the Fraction:
To eliminate the fraction, multiply both sides of the equation by 2:
n(n−1)=90
4. Rearranging the Equation:
Rearranging gives us a quadratic equation:
n2−n−90=0
5. Factoring the Quadratic:
We need to factor the quadratic equation. We look for two numbers that multiply to -90 and add to -1. The numbers -10 and 9 work:
(n−10)(n+9)=0
6. Finding the Values of n:
Setting each factor to zero gives us:
n−10=0⇒n=10
n+9=0⇒n=−9(not valid since n must be positive)
7. Conclusion:
The only valid solution is n=10. Therefore, the number of participants in the chess tournament is 10.
Final Answer:
The number of participants is 10.
Each contestant plays against every other contestant exactly once. If there are n contestants, the number of games played can be represented by the combination formula (n2), which gives the number of ways to choose 2 contestants from n.
We know that the total number of games played is 45. Therefore, we can set up the equation:
(n2)=45
This can be expanded to:
n(n−1)2=45
To eliminate the fraction, multiply both sides of the equation by 2:
n(n−1)=90
Rearranging gives us a quadratic equation:
n2−n−90=0
We need to factor the quadratic equation. We look for two numbers that multiply to -90 and add to -1. The numbers -10 and 9 work:
(n−10)(n+9)=0
Setting each factor to zero gives us:
n−10=0⇒n=10
n+9=0⇒n=−9(not valid since n must be positive)
The only valid solution is n=10. Therefore, the number of participants in the chess tournament is 10.
The number of participants is 10.
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Chapter Test
60 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Section II - Assertion Reason Type
9 Videos
- PARABOLABOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PARABOLAEXERCISE - Chapter Test
30 Videos
- PROBABILITY BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROBABILITY EXERCISE - Chapter Test
45 Videos
Similar Questions
In a class tournament where the participants were to play one game with one another, two of the class players fell ill, having played 3 games each. If the total number of games played is 24, then the number of participants at the beginning was
View SolutionTwo women and some men participated in a chess tournament in which every participant played two games with each of the other participants. If the number of games that the men played between themselves exceeds the number of games that the men played with the women by 66, then the number of men who participated in the tournament lies in the interval
View SolutionThere are m men and two women participating in a chess tournament. Each participant plays two games with every other participant. If the number of games played by the men between themselves exceeds the number of games played between the men and the women by 84, then teh value of m is
View SolutionThere are 2 women participating in a chess tournament. Every participant played 2 games with the other participants. The number of games that the men played between themselves exceeded by 66 as compared to the number of games that the men played with women. If the number of participants is n , then the value of n−6 is ______.
View SolutionThere were two women participating in a chess tournament. Every participant played two games with the other participants. The number of games that the men played among themselves proved to exceed by 66 number of games that the men played with the women. The number of participants is a. 6 b. 11 c. 13 d. none of these
View SolutionIn a class tournament, all participants were to plan different game with one another. Two players fell ill after having played three games each. If the total number of games played in the tournament is equal to 84, the total number of participants in the beginning was equal to a. 10 b. 15 c. 12 d. 14
View SolutionTwenty-eight games were played in a football tournament with each team playing once against each other. How many teams were there?
View SolutionThirty six games were played in a football tournament with each team playing once against each other. How many teams were there?
View Solution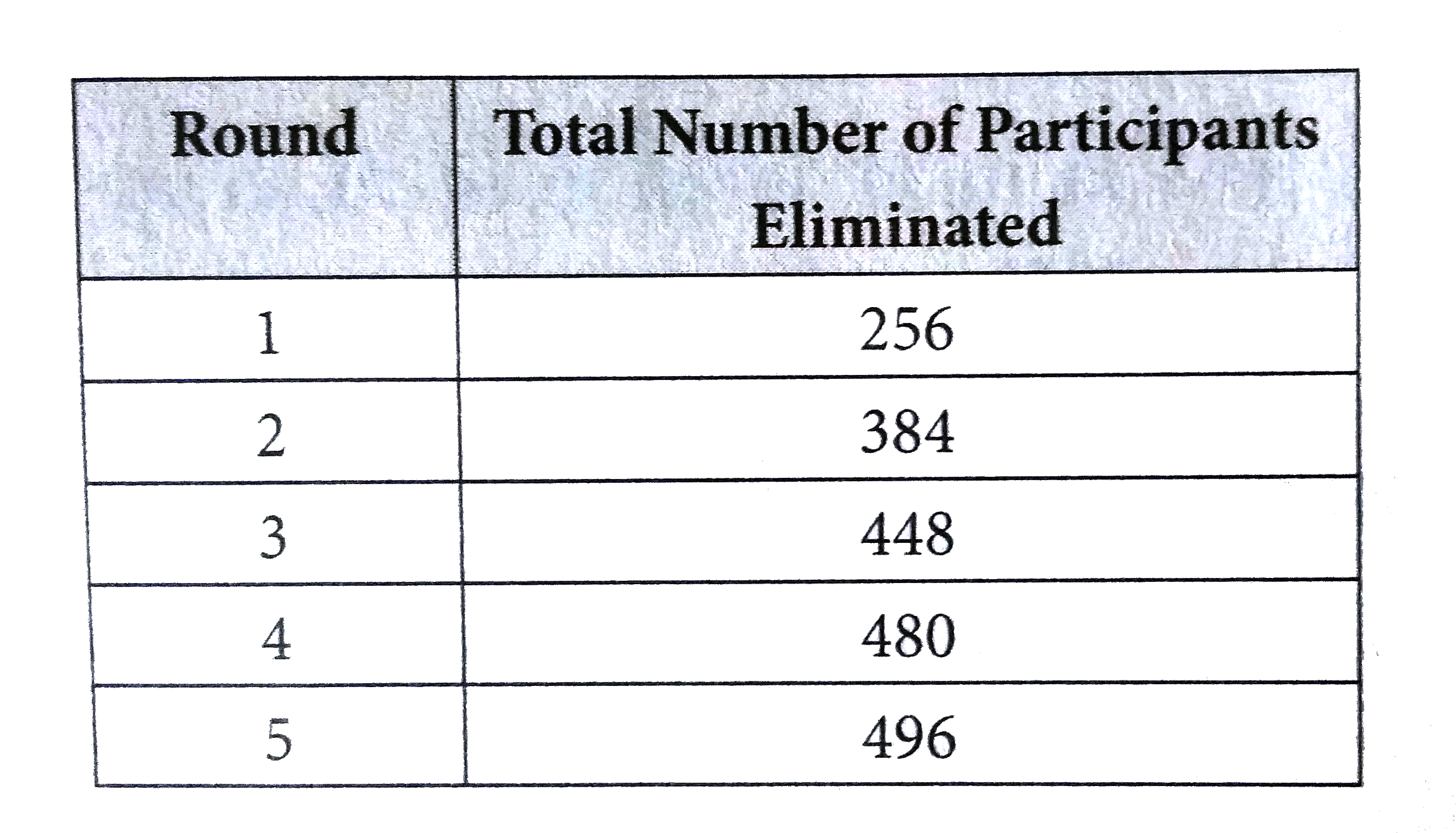
The table above shows the cummulative number of participants eliminated in a national miniature golf tournament by the end of each round. Which of the following best describes the relationship between the round and the number of participants remaining in the tournament?
View SolutionThe members of a chess club took part in a round robin competition in which each player plays with other once. All members scored the same number of points, except four juniors whose total score ere 17.5. How many members were there in the club? Assume that for each win a player scores 1 point, 1/2 for a draw, and zero for losing.
View Solution
