Column I Column II Total number of function f:{1,2,3,4,5}−−−−−−−−→1,2,3,4,5 than are on to and f(i)≠ is equal to p. divisible by 11 If x1,x2x3=2×5×72, then the number of solution set for (x1,x2,x3)wherex1∈N,x1>1 is q. divisible by 7 Number of factors of 3780 are divisible b; either 3 or 2 both is r. divisible by 3 Total number of divisor of n=25×34×510 that are of the form 4λ+2,λ≥1 is s. divisible by 4
Step by step video & image solution for Column I Column II Total number of function f:{1,2,3,4,5}vec{1,2,3,4,5} than are on to and f(i)!= is equal to p. divisible by 11 If x_1, x_2x_3=2xx5xx7^2, then the number of solution set for (x_1, x_2, x_3)w h e r ex_1 in N ,x_1>1 is q. divisible by 7 Number of factors of 3780 are divisible b; either 3 or 2 both is r. divisible by 3 Total number of divisor of n=2^5xx3^4xx5^(10) that are of the form 4lambda+2,lambdageq1 is s. divisible by 4 by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A function is defined as f:[a1,a2,a3,a4,a5,a6]−−−−−−→b1,b2,b3. Column I, Column II Number of subjective functions, p. is divisible by 9 Number of functions in which f(ai)≠bi , q. is divisible by 5 Number of invertible functions, r. is divisible by 4 Number of many be functions, s. is divisible by 3 , t. not possible
View SolutionFind the number of polynomials of the form x3+ax2+bx+c that are divisible by x2+1,wherea,b,c∈{1,2,3,9,10}.
View Solution
Knowledge Check
The solution set of 2x+13<3x−25x∈R on the number line is
A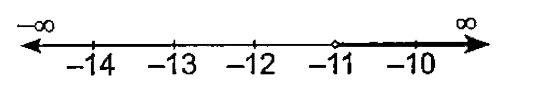 B
B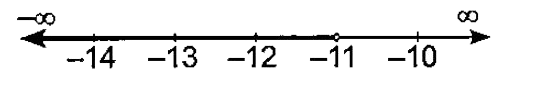 C
C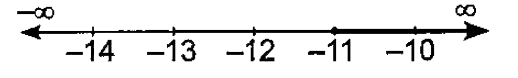 D
D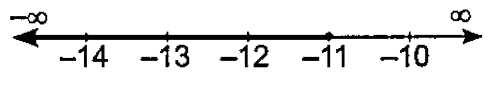
Statement -1 for all natural numbers n , 2.7n+3.5n−5 is divisible by 24.
Statement -2 if f(x) is divisible by x, then f(x+1)−f(x) is divisible by x+1,∀x∈N.
View SolutionStatement-1: If N the number of positive integral solutions of x1x2x3x4=770, then N is divisible by 4 distinct prime numbers.
Statement-2: Prime numbers are 2,3,5,7,11,13, . .
View SolutionLet P(x) and Q(x) be two polynomials.Suppose that f(x)=P(x3)+xQ(x3) is divisible by x2+x+1, then (a) P(x) is divisible by (x-1),but Q(x) is not divisible by x -1 (b) Q(x) is divisible by (x-1), but P(x) is not divisible by x-1 (c) Both P(x) and Q(x) are divisible by x-1 (d) f(x) is divisible by x-1
View SolutionThe number of polynomials of the form x3+ax2+bx+c that are divisible by x2+1, where a,b,c∈{1,2,3,4,5,6,7,8,9,10}, is
View SolutionStatement-1: A 5-digit number divisible by 3 is to be formed using the digits 0,1,2,3,4,5 without repetition, then the total number of ways this can be done is 216. Statement-2: A number is divisible by 3, if sum of its digits is divisible by 3.
View SolutionLet f(x)=ax3+5x2−bx+1. If f(x) when divied by 2x + 1 leaves 5 as remainder, and f'(x) is divisible by 3x - 1, then
View SolutionConsider a number N = 2 1 P 5 3 Q 4. The number of ordered pairs (P,Q) so that the number 'N' is divisible by 44, is
View Solution
