Find the number of integral solutions of x1+x2+x3+=24 subjected to the condition that 1≤x1≤5,12≤x2≤18 and −1≤x3
To find the number of integral solutions of the equation x1+x2+x3=24 under the given constraints, we can follow these steps:
Step 1: Rewrite the variables
We need to adjust the variables to account for the given constraints:
- Let y1=x1−1 (since x1 must be at least 1, y1 will be non-negative and can take values from 0 to 4).
- Let y2=x2−12 (since x2 must be at least 12, y2 will be non-negative and can take values from 0 to 6).
- Let y3=x3+1 (since x3 must be greater than -1, y3 will be non-negative).
Now, we can rewrite the equation:
(y1+1)+(y2+12)+(y3−1)=24
This simplifies to:
y1+y2+y3+12=24
Thus,
y1+y2+y3=12
Step 2: Determine the bounds for y1, y2, and y3
From the transformations:
- y1 can take values from 0 to 4 (since x1 can be from 1 to 5).
- y2 can take values from 0 to 6 (since x2 can be from 12 to 18).
- y3 has no upper limit (since x3 can take any value greater than -1).
Step 3: Count the solutions without restrictions
First, we calculate the total number of non-negative integer solutions to y1+y2+y3=12 without considering the upper limits on y1 and y2. The number of solutions is given by the stars and bars theorem:
Number of solutions=(n+k−1k−1)
where n is the total (12) and k is the number of variables (3):
Number of solutions=(12+3−13−1)=(142)=91
Step 4: Subtract the cases where y1 or y2 exceed their limits
1. Case 1: y1>4
- Let y′1=y1−5 (where y′1≥0). The equation becomes:
y′1+5+y2+y3=12⟹y′1+y2+y3=7
The number of solutions is:
(7+3−13−1)=(92)=36
2. Case 2: y2>6
- Let y′2=y2−7 (where y′2≥0). The equation becomes:
y1+y′2+7+y3=12⟹y1+y′2+y3=5
The number of solutions is:
(5+3−13−1)=(72)=21
3. Case 3: Both y1>4 and y2>6
- Let y′1=y1−5 and y′2=y2−7. The equation becomes:
y′1+5+y′2+7+y3=12⟹y′1+y′2+y3=0
The only solution is y′1=0,y′2=0,y3=0, which gives us 1 solution.
Step 5: Apply the principle of inclusion-exclusion
Now, we can apply the principle of inclusion-exclusion to find the total number of valid solutions:
Total valid solutions=91−36−21+1=35
Final Answer
Thus, the number of integral solutions of x1+x2+x3=24 under the given constraints is 35.
---
We need to adjust the variables to account for the given constraints:
- Let y1=x1−1 (since x1 must be at least 1, y1 will be non-negative and can take values from 0 to 4).
- Let y2=x2−12 (since x2 must be at least 12, y2 will be non-negative and can take values from 0 to 6).
- Let y3=x3+1 (since x3 must be greater than -1, y3 will be non-negative).
(y1+1)+(y2+12)+(y3−1)=24
This simplifies to:
y1+y2+y3+12=24
Thus,
y1+y2+y3=12
From the transformations:
- y1 can take values from 0 to 4 (since x1 can be from 1 to 5).
- y2 can take values from 0 to 6 (since x2 can be from 12 to 18).
- y3 has no upper limit (since x3 can take any value greater than -1).
First, we calculate the total number of non-negative integer solutions to y1+y2+y3=12 without considering the upper limits on y1 and y2. The number of solutions is given by the stars and bars theorem:
Number of solutions=(n+k−1k−1)
where n is the total (12) and k is the number of variables (3):
Number of solutions=(12+3−13−1)=(142)=91
1. Case 1: y1>4
- Let y′1=y1−5 (where y′1≥0). The equation becomes:
y′1+5+y2+y3=12⟹y′1+y2+y3=7
The number of solutions is:
(7+3−13−1)=(92)=36
- Let y′2=y2−7 (where y′2≥0). The equation becomes:
y1+y′2+7+y3=12⟹y1+y′2+y3=5
The number of solutions is:
(5+3−13−1)=(72)=21
- Let y′1=y1−5 and y′2=y2−7. The equation becomes:
y′1+5+y′2+7+y3=12⟹y′1+y′2+y3=0
The only solution is y′1=0,y′2=0,y3=0, which gives us 1 solution.
Now, we can apply the principle of inclusion-exclusion to find the total number of valid solutions:
Total valid solutions=91−36−21+1=35
Thus, the number of integral solutions of x1+x2+x3=24 under the given constraints is 35.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The solution set of 2x+13<3x−25x∈R on the number line is
A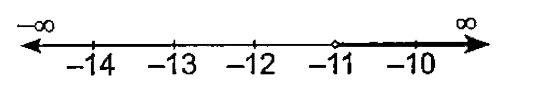 B
B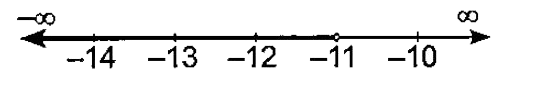 C
C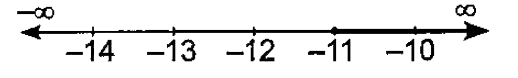 D
D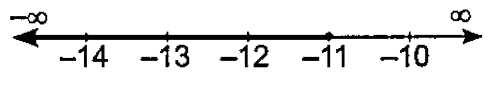
The number of intergal values of x if 5x−1<(x+1)2<7x−3 is
View SolutionSolve the following 1≤|x−2|≤3
View SolutionSolve 1≤|x−2|≤3.
View SolutionFind the solution set of each of the following inequations : −5<x2−3<52,x∈Z
View SolutionSolution set of (5x−1)<(x+1)2<(7x−3) is
View SolutionConsider any set of observations x1,x2,x3,..,x101. It is given that x1<x2<x3<..Ltx100<x101, then the mean deviation of this set of observations about a point k is minimum when k equals
View SolutionSolve: 0<|x−1|<3
View Solution
