In how many ways can a team of 6 horses be selected out of a stud of 16, so that there shall always be three out of A B C A' B' C', but never A A', B B' or C C' together a. b. c. d.
To solve the problem of selecting a team of 6 horses from a stud of 16, with specific conditions, we can break down the solution into clear steps.
1. Identify the Groups: We have 16 horses in total, which include 6 specific horses: A, A', B, B', C, and C'. The remaining horses are 10 in number.
2. Selection Requirement: We need to select 6 horses such that:
- At least 3 horses must be from the group {A, A', B, B', C, C'}.
- Horses A and A', B and B', C and C' cannot be selected together.
3. Selecting 3 Horses from the Group: Since we need to select 3 horses from the group {A, A', B, B', C, C'}, we can denote the selection as follows:
- We can choose either A or A', either B or B', and either C or C'. This gives us 2 choices for each of the 3 pairs.
4. Calculate the Combinations: The total number of ways to select one horse from each pair (A, A'), (B, B'), and (C, C') is:
2×2×2=8
5. Selecting the Remaining Horses: After selecting 3 horses from the group {A, A', B, B', C, C'}, we need to select 3 more horses from the remaining 10 horses. The number of ways to choose 3 horses from 10 is given by the combination formula:
(103)
6. Calculate (103):
(103)=10×9×83×2×1=7206=120
7. Total Combinations: Now, we multiply the number of ways to select the horses from the two groups:
Total Ways=(103)×8=120×8=960
Final Answer:
The total number of ways to select the team of 6 horses under the given conditions is 960.
- At least 3 horses must be from the group {A, A', B, B', C, C'}.
- Horses A and A', B and B', C and C' cannot be selected together.
- We can choose either A or A', either B or B', and either C or C'. This gives us 2 choices for each of the 3 pairs.
2×2×2=8
(103)
(103)=10×9×83×2×1=7206=120
Total Ways=(103)×8=120×8=960
The total number of ways to select the team of 6 horses under the given conditions is 960.
Topper's Solved these Questions
Similar Questions
In how many ways can a team of 11 players be formed out of 25 players, if 6 out of them are always to be included and 5 always to be excluded a. 2020 b. 2002 c. 2008 d. 8002
View SolutionIn how many ways can the 7 letters A, B, C, D, E, F, and G be arranged so that C and E are never together?
View SolutionThere are 6 students A,B,C,D,E,F. In how many ways can they be seated in a line so that C and D do not sit together?
View SolutionGive an example of three matrices A, B, C such that AB=AC but B≠C .
View SolutionGive an example of three matrices A, B, C such that AB=AC but B≠C .
View SolutionThere are 6 students A,B,C,D,E,F. In how many ways can a committee of 4 be formed so as to always include C?
View SolutionThere are 6 students A,B,C,D,E,F. In hoiw many ways can a committee of 4 be formed so as to always include C but exclude E?
View SolutionSelect the correct labelling out of a, b c and d of mitochondrian
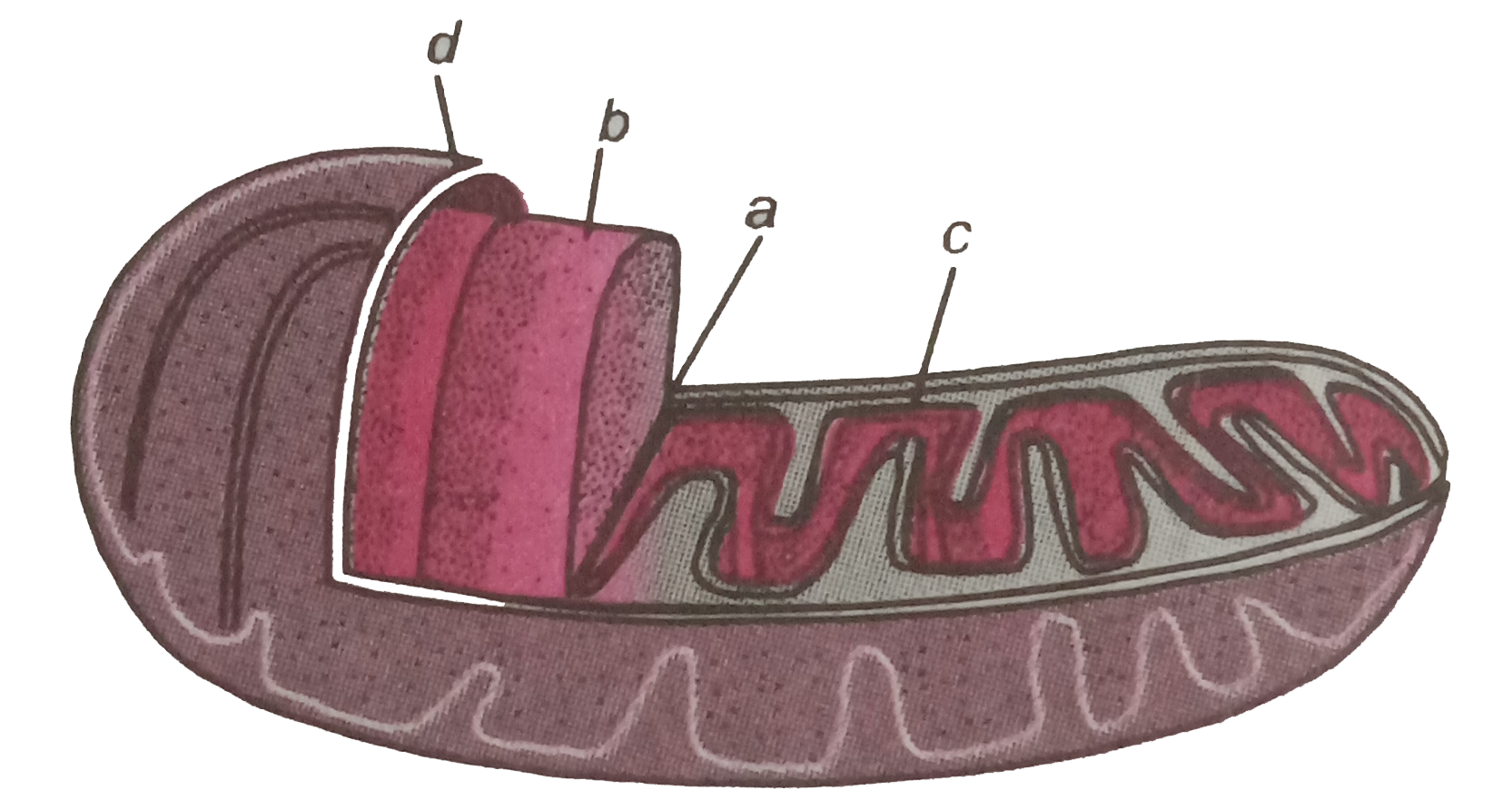
View SolutionIn a ABC, BD and CE are the altitudes. Prove that ADB and AEC are similar. Is CDB~BEC ?
View SolutionThe perpendicular AD on the base BC of a triangle ABC intersects BC at D so that DB=3CD . Prove that 2 AB2=2 AC2+BC2 .
View Solution
