If fogoh(x) is an increasing function, then which of the following is not possible? (a)f(x),g(x),andh(x) are increasing (b)f(x)andg(x) are decreasing and h(x) is increasing (c)f(x),g(x),andh(x) are decreasing
To determine which of the given options is not possible when f(g(h(x))) is an increasing function, we need to analyze the implications of the derivatives of the functions involved.
1. Understanding the Condition:
- We know that f(g(h(x))) is an increasing function. This means that the derivative of f(g(h(x))) must be greater than zero:
ddx(f(g(h(x))))>0
2. Applying the Chain Rule:
- By applying the chain rule, we can express the derivative as:
f′(g(h(x)))⋅g′(h(x))⋅h′(x)>0
- This means that the product of the derivatives f′(g(h(x))), g′(h(x)), and h′(x) must be positive.
3. Analyzing Each Option:
- Option A: f(x),g(x),h(x) are all increasing.
- If f′,g′,h′>0, then the product f′⋅g′⋅h′>0. This option is possible.
- Option B: f(x),g(x) are decreasing and h(x) is increasing.
- If f′,g′<0 and h′>0, then the product f′⋅g′⋅h′<0. This option is also possible because the two negative derivatives can multiply to give a positive result when combined with a positive derivative.
- Option C: f(x),g(x),h(x) are all decreasing.
- If f′,g′,h′<0, then the product f′⋅g′⋅h′<0. This option is not possible because the product of three negative numbers cannot be positive.
4. Conclusion:
- The option that is not possible is Option C: f(x),g(x),h(x) are all decreasing.
Final Answer:
The correct option that is not possible is (c) f(x),g(x),h(x) are decreasing.
- We know that f(g(h(x))) is an increasing function. This means that the derivative of f(g(h(x))) must be greater than zero:
ddx(f(g(h(x))))>0
- By applying the chain rule, we can express the derivative as:
f′(g(h(x)))⋅g′(h(x))⋅h′(x)>0
- This means that the product of the derivatives f′(g(h(x))), g′(h(x)), and h′(x) must be positive.
- Option A: f(x),g(x),h(x) are all increasing.
- If f′,g′,h′>0, then the product f′⋅g′⋅h′>0. This option is possible.
- Option B: f(x),g(x) are decreasing and h(x) is increasing.
- If f′,g′<0 and h′>0, then the product f′⋅g′⋅h′<0. This option is also possible because the two negative derivatives can multiply to give a positive result when combined with a positive derivative.
- Option C: f(x),g(x),h(x) are all decreasing.
- If f′,g′,h′<0, then the product f′⋅g′⋅h′<0. This option is not possible because the product of three negative numbers cannot be positive.
- The option that is not possible is Option C: f(x),g(x),h(x) are all decreasing.
The correct option that is not possible is (c) f(x),g(x),h(x) are decreasing.
Similar Questions
If f(x)andg(x) are two positive and increasing functions, then which of the following is not always true? (a) [f(x)]g(x) is always increasing (b) [f(x)]g(x) is decreasing, when f(x)<1 (c) [f(x)]g(x) is increasing, then f(x)>1. (d) If f(x)>1,then[f(x)]g(x) is increasing.
View SolutionIf f(x) and g(x) are differentiable and increasing functions then which of the following functions alwasys increases?
View SolutionFind the intervals in which the following function is increasing and decreasing f(x)=x2−6x+7
View SolutionFind the intervals in which the following functions are:
(i) increasing
.(ii)decreasing f(x)=2x2−6x
View SolutionFor each of the following graphs, comment whether f(x) is increasing or decreasing or neither increasing nor decreasing at x = a.
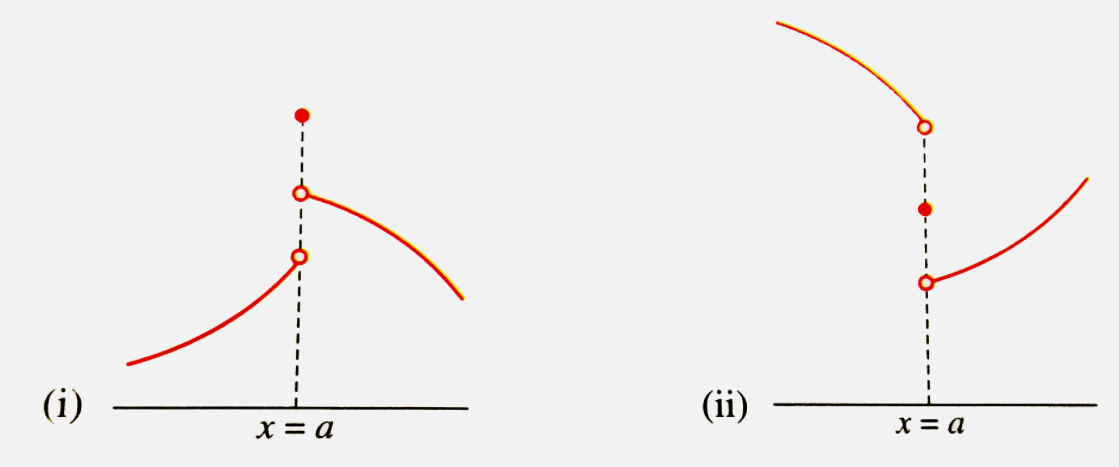
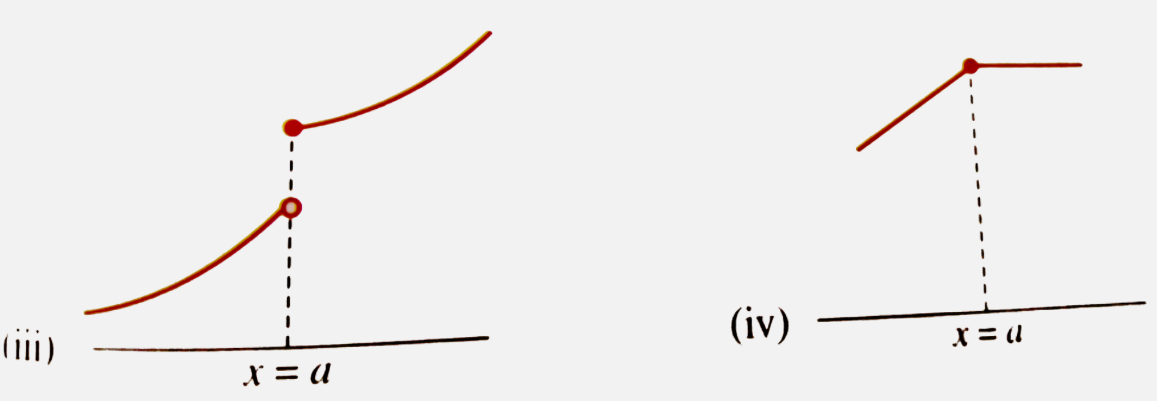
View SolutionIf f(x)=xex(x−1) , then f(x) is
View SolutionFind the intervals in which f(x)=xlogx is increasing or decreasing
View SolutionStatement 1: The function f(x)=x In x is increasing in (1e,∞) Statement 2: If both f(x)andg(x) are increasing in (a,b),thenf(x)g(x) must be increasing in (a,b).
View SolutionFind the intervals in which f(x)=xlogx is increasing or decreasing.
View SolutionWhich of the following statement is always true? (a)If f(x) is increasing, the f−1(x) is decreasing. (b)If f(x) is increasing, then 1f(x) is also increasing. (c)If fandg are positive functions and f is increasing and g is decreasing, then fg is a decreasing function. (d)If fandg are positive functions and f is decreasing and g is increasing, the fg is a decreasing function.
View Solution
