Which of the following statement is always true? (a)If f(x) is increasing, the f−1(x) is decreasing. (b)If f(x) is increasing, then 1f(x) is also increasing. (c)If fandg are positive functions and f is increasing and g is decreasing, then fg is a decreasing function. (d)If fandg are positive functions and f is decreasing and g is increasing, the fg is a decreasing function.
To determine which of the statements is always true, we will analyze each option step by step.
Step 1: Analyze Option (a)
Statement: If f(x) is increasing, then f−1(x) is decreasing.
1. Definition of Increasing Function: A function f(x) is increasing if for any two points x1<x2, we have f(x1)<f(x2).
2. Inverse Function: If f(x) is increasing, then its inverse f−1(x) will also be increasing. This is because if f(a)<f(b), then a<b implies f−1(f(a))<f−1(f(b)).
3. Conclusion for (a): Therefore, this statement is false.
Step 2: Analyze Option (b)
Statement: If f(x) is increasing, then 1f(x) is also increasing.
1. Increasing Function: Since f(x) is increasing, f'(x)>0.
2. Function Transformation: Consider the function h(x)=1f(x).
3. Derivative of h(x): Using the quotient rule, we find:
\(
h'(x) = -\frac{f'(x)}{(f(x))^2}
\)
Since f'(x)>0 and f(x)>0, we have h'(x)<0. This means h(x) is decreasing.
4. Conclusion for (b): Therefore, this statement is false.
Step 3: Analyze Option (c)
Statement: If f and g are positive functions and f is increasing and g is decreasing, then fg is a decreasing function.
1. Increasing and Decreasing Functions: Given f'(x)>0 and g'(x)<0.
2. Function Transformation: Let h(x)=f(x)g(x).
3. Derivative of h(x): Using the quotient rule:
\(
h'(x) = \frac{g(x)f'(x) - f(x)g'(x)}{(g(x))^2}
\)
Here, since g(x)>0, the sign of h'(x) depends on the numerator:
- g(x)f'(x)>0 (since both are positive)
- −f(x)g'(x)>0 (since g'(x)<0 and f(x)>0)
- Therefore, h'(x)>0, meaning h(x) is increasing.
4. Conclusion for (c): Therefore, this statement is false.
Step 4: Analyze Option (d)
Statement: If f and g are positive functions and f is decreasing and g is increasing, then fg is a decreasing function.
1. Decreasing and Increasing Functions: Given f'(x)<0 and g'(x)>0.
2. Function Transformation: Let h(x)=f(x)g(x).
3. Derivative of h(x): Using the quotient rule:
\(
h'(x) = \frac{g(x)f'(x) - f(x)g'(x)}{(g(x))^2}
\)
Here, since g(x)>0, the sign of h'(x) depends on the numerator:
- g(x)f'(x)<0 (since f'(x)<0)
- −f(x)g'(x)<0 (since g'(x)>0 and f(x)>0)
- Therefore, h'(x)<0, meaning h(x) is decreasing.
4. Conclusion for (d): Therefore, this statement is true.
Final Conclusion
The only statement that is always true is Option (d).
Statement: If f(x) is increasing, then f−1(x) is decreasing.
2. Inverse Function: If f(x) is increasing, then its inverse f−1(x) will also be increasing. This is because if f(a)<f(b), then a<b implies f−1(f(a))<f−1(f(b)).
3. Conclusion for (a): Therefore, this statement is false.
Statement: If f(x) is increasing, then 1f(x) is also increasing.
2. Function Transformation: Consider the function h(x)=1f(x).
3. Derivative of h(x): Using the quotient rule, we find:
\(
h'(x) = -\frac{f'(x)}{(f(x))^2}
\)
Since f'(x)>0 and f(x)>0, we have h'(x)<0. This means h(x) is decreasing.
4. Conclusion for (b): Therefore, this statement is false.
Statement: If f and g are positive functions and f is increasing and g is decreasing, then fg is a decreasing function.
2. Function Transformation: Let h(x)=f(x)g(x).
3. Derivative of h(x): Using the quotient rule:
\(
h'(x) = \frac{g(x)f'(x) - f(x)g'(x)}{(g(x))^2}
\)
Here, since g(x)>0, the sign of h'(x) depends on the numerator:
- g(x)f'(x)>0 (since both are positive)
- −f(x)g'(x)>0 (since g'(x)<0 and f(x)>0)
- Therefore, h'(x)>0, meaning h(x) is increasing.
4. Conclusion for (c): Therefore, this statement is false.
Statement: If f and g are positive functions and f is decreasing and g is increasing, then fg is a decreasing function.
2. Function Transformation: Let h(x)=f(x)g(x).
3. Derivative of h(x): Using the quotient rule:
\(
h'(x) = \frac{g(x)f'(x) - f(x)g'(x)}{(g(x))^2}
\)
Here, since g(x)>0, the sign of h'(x) depends on the numerator:
- g(x)f'(x)<0 (since f'(x)<0)
- −f(x)g'(x)<0 (since g'(x)>0 and f(x)>0)
- Therefore, h'(x)<0, meaning h(x) is decreasing.
4. Conclusion for (d): Therefore, this statement is true.
The only statement that is always true is Option (d).
Similar Questions
The function f(x)=x2−x+1 is increasing and decreasing in the intervals
View SolutionIf f is decreasing and g is increasing functions such that gof exists then gof is
View SolutionIf f and g are two increasing function such that fog is defined then
View SolutionProve that the function f(x)=cosx is neither increasing nor decreasing in (0, 2π)
View Solutionif f is an increasing function and g is a decreasing function on an interval I such that fog exists then
View SolutionThe function f and g are positive and continuous. If f is increasing and g is decreasing, then ∫10f(x)[g(x)−g(1−x)]dx is always non-positive is always non-negative can take positive and negative values none of these
View SolutionProve that the function f(x)=x2−x+1 is neither increasing nor decreasing on (−1, 1) .
View SolutionFor each of the following graphs, comment whether f(x) is increasing or decreasing or neither increasing nor decreasing at x = a.
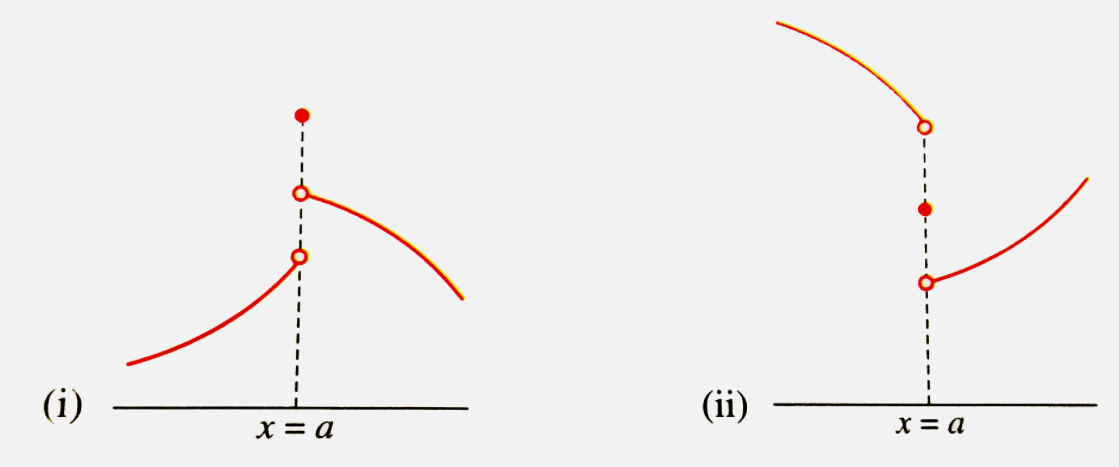
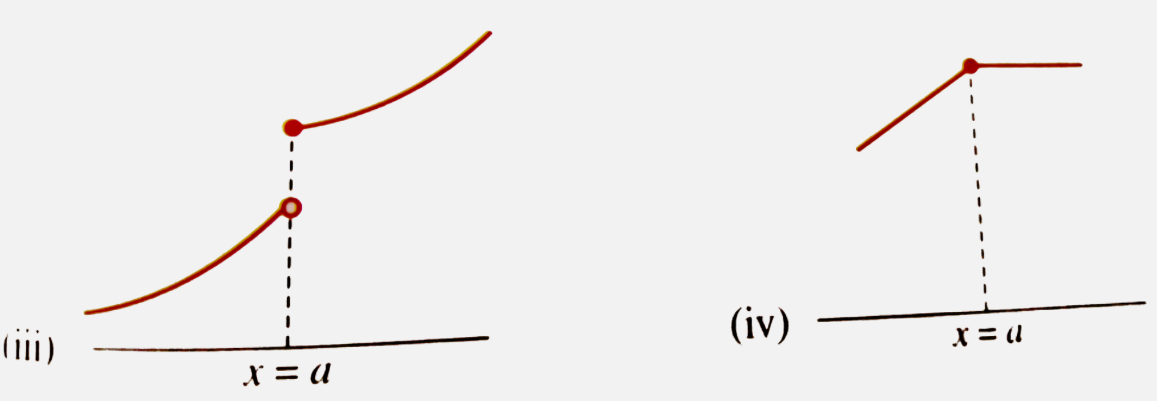
View SolutionFind the intervals in which the following function is increasing and decreasing f(x)=x2−6x+7
View SolutionShow that f(x)=cosx is decreasing function on (0,π), increasing in (−π,0) and neither increasing nor decreasing in (−π,π).
View Solution
