A right triangle is drawn in a semicircle of radius 12 with one of its legs along the diameter. If the maximum area of the triangle is M , then the value of 32√3Mc is______
To solve the problem of finding the maximum area M of a right triangle inscribed in a semicircle of radius 12 with one leg along the diameter, we can follow these steps:
Step 1: Understand the Geometry
We have a semicircle with radius r=12. The diameter of the semicircle will be 2r=1. Let the points on the diameter be A(−12,0) and B(12,0), and let point C be the vertex of the triangle on the semicircle.
Step 2: Set Up the Coordinates
Let the coordinates of point C be (x,y). Since point C lies on the semicircle, it satisfies the equation of the semicircle:
x2+y2=r2⟹x2+y2=(12)2=14
Step 3: Express Area of the Triangle
The area A of triangle ABC can be expressed as:
A=12×base×height=12×AB×y=12×1×y=y2
Step 4: Express y in Terms of x
From the semicircle equation, we can express y in terms of x:
y=√14−x2
Thus, the area can be rewritten as:
A=12√14−x2
Step 5: Maximize the Area
To find the maximum area, we need to maximize A:
A=12√14−x2
To do this, we can differentiate A with respect to x and set the derivative to zero.
Step 6: Differentiate and Solve
Let A=12√14−x2. The derivative A′ is:
A′=12⋅12⋅−2x√14−x2=−x√14−x2
Setting A′=0 gives x=0.
Step 7: Find the Corresponding y
Substituting x=0 back into the semicircle equation:
y=√14−02=12
Step 8: Calculate Maximum Area
Now substituting y into the area formula:
M=12×12=14
Step 9: Calculate 32√3M
Finally, we need to find:
32√3M=32√3×14=8√3
Final Answer
Thus, the value of 32√3M is:
8√3
We have a semicircle with radius r=12. The diameter of the semicircle will be 2r=1. Let the points on the diameter be A(−12,0) and B(12,0), and let point C be the vertex of the triangle on the semicircle.
Let the coordinates of point C be (x,y). Since point C lies on the semicircle, it satisfies the equation of the semicircle:
x2+y2=r2⟹x2+y2=(12)2=14
The area A of triangle ABC can be expressed as:
A=12×base×height=12×AB×y=12×1×y=y2
From the semicircle equation, we can express y in terms of x:
y=√14−x2
Thus, the area can be rewritten as:
A=12√14−x2
To find the maximum area, we need to maximize A:
A=12√14−x2
To do this, we can differentiate A with respect to x and set the derivative to zero.
Let A=12√14−x2. The derivative A′ is:
A′=12⋅12⋅−2x√14−x2=−x√14−x2
Setting A′=0 gives x=0.
Substituting x=0 back into the semicircle equation:
y=√14−02=12
Now substituting y into the area formula:
M=12×12=14
Finally, we need to find:
32√3M=32√3×14=8√3
Thus, the value of 32√3M is:
8√3
Similar Questions
An equilateral triangle is drawn on a diagonal of a square of perimeter 16cm. If the area of triangle is x√3cm2, then the value of x is
View SolutionA small card is in the shape of an isosceles triangle with a semicircle on its base. If the diameter of the semicircle is 6 cm, and the hright of the triangle is 3 cm, find the area of the card.
View Solution
Knowledge Check
A right triangle , shown below , has a longer leg measing 16√3 centimeters . How long is the hypotenuse of the triangle , in centimeters ?
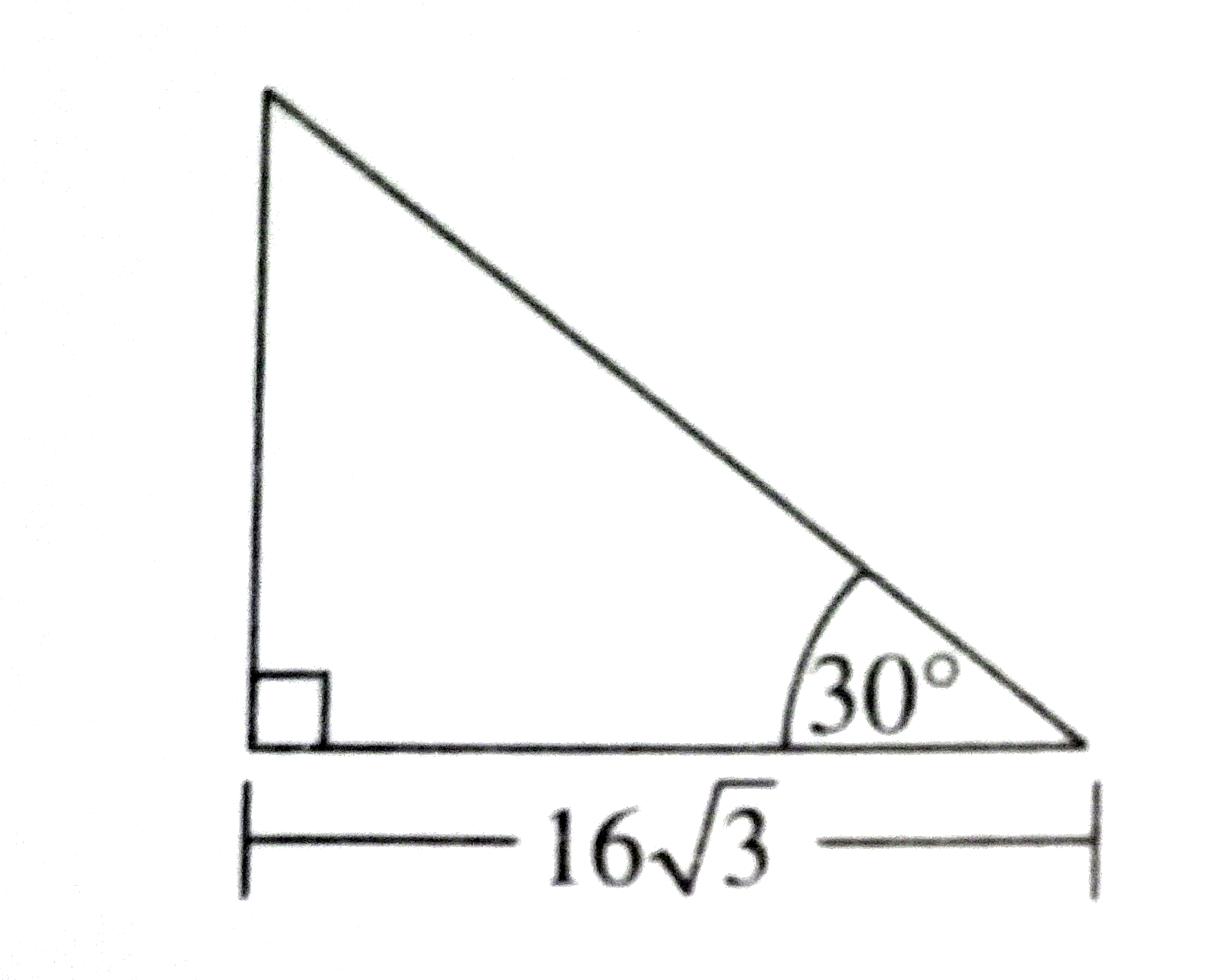 A8B8√2C16D32
A8B8√2C16D32
The area of a right triangle is 6864 sq. units. If the ratio of its legs is 143:24, then the value of r is ______
View SolutionThe three sides of a trapezium are equal each being 6 cms long. Let Δcm2 be the maximum area of the trapezium. The value of √3Δ is :
View SolutionIn a ΔABC, a semicircle is inscribed, whose diameter lies on the side c. Then the radius of the semicircle is (Where Δ is the area of the triangle ABC)
View SolutionConsider a right triangle with legs of length a and b and hypotenuse of lengthc. If k denotes the area of the triangle then the value of (a+b) equals
View SolutionThe base and the height of a triangle are in the ratio 5:3. If the area of the triangle is 67.5 m2, find its base and height.
View SolutionThe lengths of the two shorter legs of a right triangle add up to 40 units. What is the maximum possible area of the triangle?
View SolutionIn the right triangle BAC,∠A=π2anda+b=8. The area of the triangle is maximum when ∠C , is
View Solution