Let h(x)=f(x)−(f(x))2+(f(x))3 for every real number x. Then (a) h is increasing whenever f is increasing (b)h is increasing whenever f is decreasing (c)h is decreasing whenever f is decreasing (d) nothing can be said in general
To solve the problem, we need to analyze the function h(x)=f(x)−(f(x))2+(f(x))3 and determine the relationship between the behavior of h and the behavior of f.
Step 1: Differentiate h(x)
We start by finding the derivative of h(x) with respect to x:
h′(x)=ddx(f(x))−ddx((f(x))2)+ddx((f(x))3)
Using the chain rule, we differentiate each term:
1. The derivative of f(x) is f′(x).
2. The derivative of (f(x))2 is 2f(x)f′(x).
3. The derivative of (f(x))3 is 3(f(x))2f′(x).
Putting it all together, we have:
h′(x)=f′(x)−2f(x)f′(x)+3(f(x))2f′(x)
Step 2: Factor out f′(x)
Now, we can factor out f′(x):
h′(x)=f′(x)(1−2f(x)+3(f(x))2)
Step 3: Analyze the expression 1−2f(x)+3(f(x))2
Let y=f(x). Then we can rewrite the expression as:
h′(x)=f′(x)(3y2−2y+1)
Now, we need to analyze the quadratic 3y2−2y+1:
1. The discriminant D of the quadratic 3y2−2y+1 is given by D=b2−4ac=(−2)2−4⋅3⋅1=4−12=−8.
2. Since the discriminant is negative, the quadratic has no real roots and opens upwards (as the coefficient of y2 is positive).
Thus, 3y2−2y+1>0 for all real y.
Step 4: Conclusion about h′(x)
Since 3f(x)2−2f(x)+1>0 for all f(x), the sign of h′(x) depends solely on the sign of f′(x):
- If f′(x)>0 (i.e., f is increasing), then h′(x)>0 (i.e., h is increasing).
- If f′(x)<0 (i.e., f is decreasing), then h′(x)<0 (i.e., h is decreasing).
Final Answer
From the analysis, we conclude that:
- h is increasing whenever f is increasing (Option a).
- h is decreasing whenever f is decreasing (Option c).
Thus, the correct options are (a) and (c).
2. The derivative of (f(x))2 is 2f(x)f′(x).
3. The derivative of (f(x))3 is 3(f(x))2f′(x).
2. Since the discriminant is negative, the quadratic has no real roots and opens upwards (as the coefficient of y2 is positive).
- If f′(x)<0 (i.e., f is decreasing), then h′(x)<0 (i.e., h is decreasing).
- h is decreasing whenever f is decreasing (Option c).
Similar Questions
Let g(x)=(f(x))3−3(f(x))2+4f(x)+5x+3sinx+4cosx∀x∈R. Then prove that g is increasing whenever is increasing.
View SolutionLet g(x)=(f(x))3−3(f(x))2+4f(x)+5x+3sinx+4cosx∀x∈R. Then prove that g is increasing whenever is increasing.
View SolutionLet h(x)=f(x)−a(f(x))3 for every real number x
h(x) increase as f(x) increses for all real values of x if
View SolutionThe function f(x)=x1+|x| is (a) strictly increasing (b) strictly decreasing (c) neither increasing nor decreasing (d) none of these
View SolutionThe function f(x)=x2−x+1 is increasing and decreasing in the intervals
View SolutionFind the intervals in which f(x)=xlogx is increasing or decreasing
View SolutionFor each of the following graphs, comment whether f(x) is increasing or decreasing or neither increasing nor decreasing at x = a.
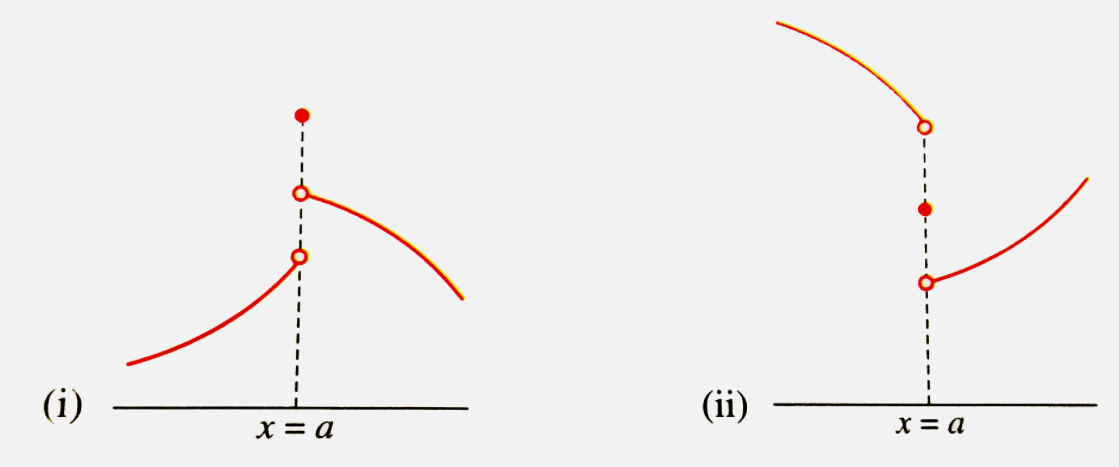
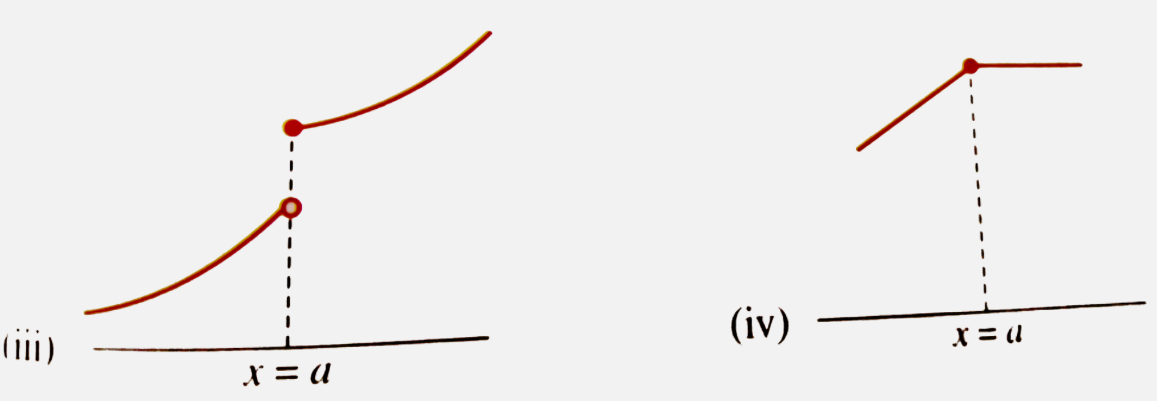
View SolutionFind the intervals in which f(x)=xlogx is increasing or decreasing.
View SolutionWhich of the following statement is always true? (a)If f(x) is increasing, the f−1(x) is decreasing. (b)If f(x) is increasing, then 1f(x) is also increasing. (c)If fandg are positive functions and f is increasing and g is decreasing, then fg is a decreasing function. (d)If fandg are positive functions and f is decreasing and g is increasing, the fg is a decreasing function.
View SolutionState whether f(x)=tanx−x is increasing or decreasing its domain.
View Solution
