If the sum of the distances of a point from two perpendicular lines in a plane is 1, then its locus is(A) a square (b) a circle (C) a straight line (d) two intersecting lines
a square
a circle
a straight line
two intersecting lines
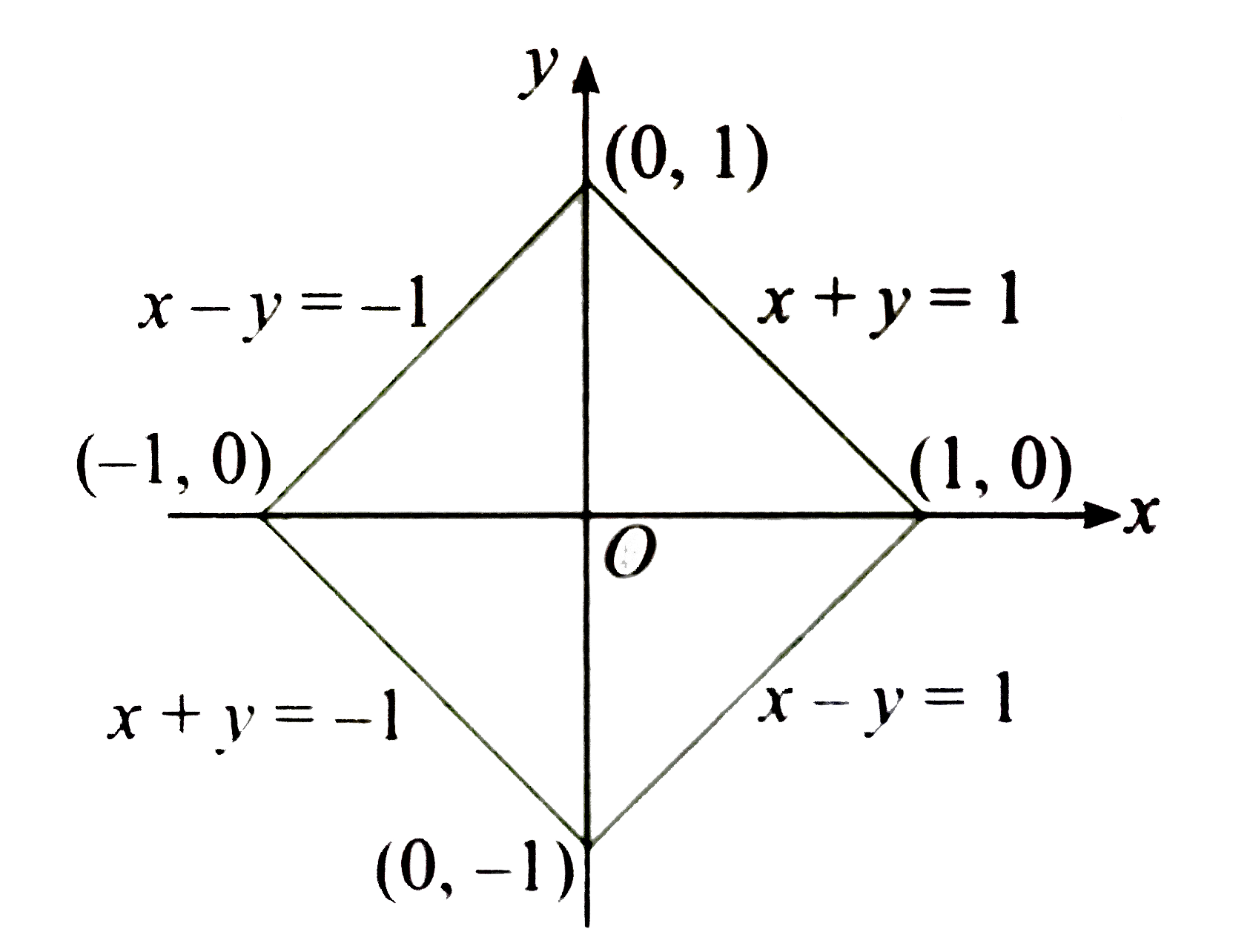
Let the two perpendicular lines be taken as the coordinates axes. If (h,k) is any point on the locus, then according to the given condition, |h|+|k|=1. Hence, the locus of (h,k) is |x|+|y|=1. This consists of four line segments enclosing a square as shown in the figure.
Topper's Solved these Questions
Similar Questions
A rod of length / slides with its ends on two perpendicular lines. Find the locus of its mid-point.
View SolutionWrite the maximum number of points of intersection of 8 straight lines in a plane.
View SolutionFind the locus of centres of circles which touch two intersecting lines.
View SolutionAn ellipse slides between two perpendicular straight lines. Then identify the locus of its center.
View SolutionA point moves so that the sum of the squares of its distances from two intersecting straight lines is constant. Prove that its locus is an ellipse.
View SolutionThe locus of a point which moves such that the sum of the square of its distance from three vertices of a triangle is constant is a/an circle (b) straight line (c) ellipse (d) none of these
View SolutionA line of fixed length a+b moves so that its ends are always on two fixed perpendicular straight lines. Then the locus of the point which divides this line into portions of length aandb is (a) an ellipse (b) parabola (c) straight line (d) none of these
View SolutionIf z2+z|z|+∣∣z2∣∣=0, then the locus z is a. a circle b. a straight line c. a pair of straight line d. none of these
View SolutionTwo particles move with constant velocities towards point O along straight lines in a plane as shown. The shortest distance A and B is
 View Solution
View SolutionProve that two lines that are respectively perpendicular to two intersecting lines intersect each other .
View Solution

