Two numbers are randomly selected and multiplied. Consider two events E1andE2 defined as E1 : Their product is divisible by 5 and E2 Unit's place in their product is 5 Which of the following statement(s) is/are correct? (a)E1 is twice as likely to occur as E2. (b) E1 and E2 are disjoint. (c) P(E1/E2)=1/4 (d) P(E1/E2)=1
To solve the problem, we need to analyze the two events E1 and E2:
- E1: The product of the two numbers is divisible by 5.
- E2: The unit's place of the product of the two numbers is 5.
Step 1: Calculate P(E1)
For E1 to occur, at least one of the two numbers must be divisible by 5. The possible numbers we can select are from 1 to 10 (assuming we are selecting from the first 10 natural numbers).
The numbers divisible by 5 in this range are 5 and 10.
- Total outcomes when selecting two numbers = 10×10=100.
- Outcomes where at least one number is divisible by 5:
- Total outcomes where neither number is divisible by 5 = 8×8=64 (the numbers 1, 2, 3, 4, 6, 7, 8, 9).
- Thus, outcomes where at least one number is divisible by 5 = 100−64=36.
So,
P(E1)=36100=925
Step 2: Calculate P(E2)
For E2 to occur, the unit's place of the product must be 5. This can happen when one number ends in 5 and the other ends in an odd number (1, 3, 5, 7, 9).
- The numbers that can end in 5 are 5 and 10.
- The odd numbers in the range are 1, 3, 5, 7, 9 (5 options).
Calculating the outcomes:
- If the first number is 5, the second number can be any of the 5 odd numbers: 1,3,5,7,9 (5 outcomes).
- If the first number is 10, the second number can also be any of the 5 odd numbers: 1,3,5,7,9 (5 outcomes).
Thus, the total outcomes for E2:
P(E2)=5+5100=10100=110
Step 3: Check if E1 and E2 are disjoint
Events E1 and E2 are disjoint if they cannot happen at the same time.
- The product can be divisible by 5 (if either number is 5 or 10) and can also end in 5 (if one number is 5 and the other is odd). Therefore, they are not disjoint.
Step 4: Calculate P(E1|E2)
Using the formula for conditional probability:
P(E1|E2)=P(E1∩E2)P(E2)
To find P(E1∩E2):
- The only way for both events to occur is if one number is 5 and the other is an odd number. This gives us 5 outcomes (as calculated above).
Thus,
P(E1∩E2)=5100=120
Now substituting into the conditional probability formula:
P(E1|E2)=120110=120×101=12
Conclusion
Now we can analyze the options:
(a) E1 is twice as likely to occur as E2. False (since P(E1)=925 and P(E2)=110).
(b) E1 and E2 are disjoint. False (as shown above).
(c) P(E1|E2)=14. False (we found it to be 12).
(d) P(E1|E2)=1. False (we found it to be 12).
Final Answer
None of the statements are correct.
- E2: The unit's place of the product of the two numbers is 5.
- Outcomes where at least one number is divisible by 5:
- Total outcomes where neither number is divisible by 5 = 8×8=64 (the numbers 1, 2, 3, 4, 6, 7, 8, 9).
- Thus, outcomes where at least one number is divisible by 5 = 100−64=36.
P(E1)=36100=925
- The odd numbers in the range are 1, 3, 5, 7, 9 (5 options).
- If the first number is 5, the second number can be any of the 5 odd numbers: 1,3,5,7,9 (5 outcomes).
- If the first number is 10, the second number can also be any of the 5 odd numbers: 1,3,5,7,9 (5 outcomes).
P(E2)=5+5100=10100=110
P(E1|E2)=P(E1∩E2)P(E2)
- The only way for both events to occur is if one number is 5 and the other is an odd number. This gives us 5 outcomes (as calculated above).
P(E1∩E2)=5100=120
P(E1|E2)=120110=120×101=12
None of the statements are correct.
Similar Questions
Two whole numbers are randomly selected and multiplied. Consider two events E1andE2 defined as E1 : Their product is divisible by 5 and E2 Unit's place in their product is 5 Which of the following statement(s) is/are correct?
View SolutionTwo batteries of emf E1 and E2(E2>E1) and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure. Then, which of the followings statements is correct ?
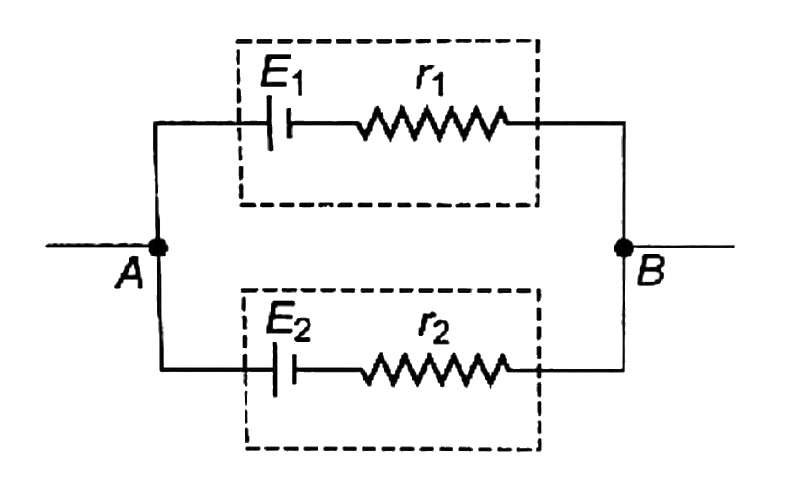
View Solution
Knowledge Check
Let E1andE2 are two mutually exclusive and exhaustive events. If odds are 2:3 against E1 then odds in favour of E2 are
A3:2B1:3C3:1D2:3
Let two fair six-faced dice A and B be thrown simultaneously. If E1 is the event that die A shows up four, E2 is the event that die B shows up two and E3 is the event that the sum of numbers on both dice is odd, then which of the following statements is NOT true ? (1) E1 and E2 are independent. (2) E2 and E3 are independent. (3) E1 and E3 are independent. (4) E1 , E2 and E3 are independent.
View SolutionFor any two independent events E1 and E2 P{(E1∪E2)∩(¯¯¯¯E1∩¯¯¯¯E2} is equal to
View SolutionIf E1 and E2 are two events such that P(E1)=1/4, P(E2/E1)=1/2 and P(E1/E2)=1/4, then
View SolutionIn the figure shown, at what distance

(a) E2 will appear to E1
(b) E1 will appear to E2
View SolutionIf E and F are two independent events and P(E)=13,P(F)=14, then find P(E∪F).
View SolutionThe letters of the word PRABABILITY are written down at random in a row. Let E1 denotes the event that two Is are together and E2 denotes the event that B's are together, then P(E1)=P(E2=311 (b) P(E1∩E2)=255 P(E1∪E2)=1855 (d) P(E1E2)=15
View SolutionTwo cells of emfs E1 and E2 and of negligible internal resistances are connected with two variable resistors as shown in Fig. A2.4. When the galvanometer shows no deflection, the values of the resistances are P and Q. What is the value of the ratio E2E1?
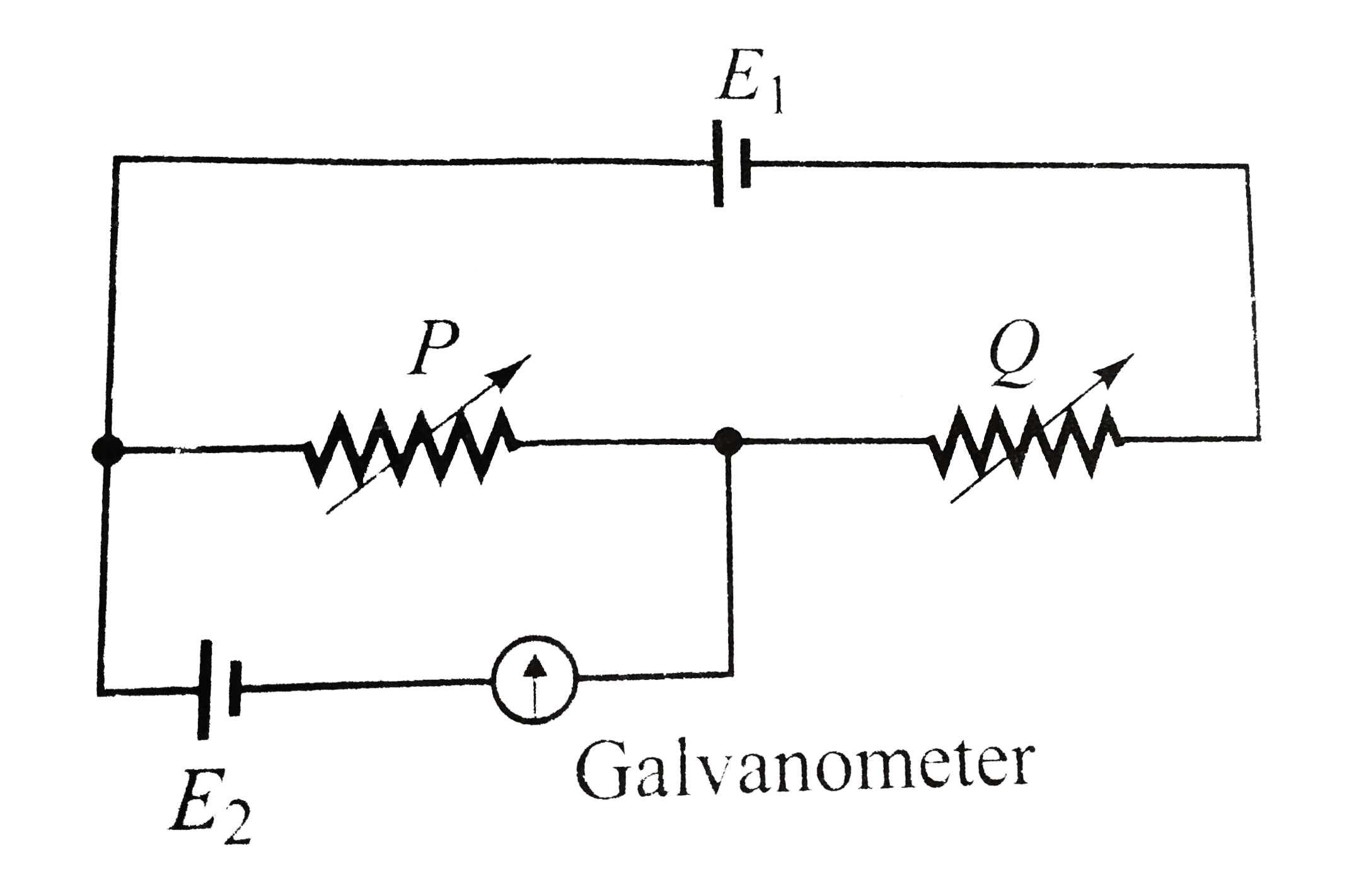
View Solution
