Column I|Column II If the circle lies in the first quadrant, then,|p. g<0 If the circle lies above the x-axis, then|q. g>0 If the circle lies on the left of the y-axis, then|r. g2−c<0 If the circle touches the positive x-axis and does not intersect the y-axis, then|s. c>0
To solve the problem, we will analyze each statement from Column I and match it with the appropriate option from Column II based on the properties of circles.
1. Statement 1: If the circle lies in the first quadrant, then:
- A circle in the first quadrant has its center at coordinates (-g, -f) where both -g and -f must be positive. This implies:
- g<0 (since -g > 0)
- f<0 (since -f > 0)
- Therefore, the correct match is p: g<0.
2. Statement 2: If the circle lies above the x-axis, then:
- For the circle to lie above the x-axis, the y-coordinate of the center (-f) must be positive, which implies:
- f<0
- The circle can touch or intersect the y-axis, which means:
- The equation when x = 0 (i.e., y2+2fy+c=0) must have real roots. Thus, f2−c≥0.
- Additionally, since it does not touch the x-axis, g2−c<0.
- Therefore, the correct match is r: g2−c<0.
3. Statement 3: If the circle lies on the left of the y-axis, then:
- The center of the circle is at (-g, -f) where -g must be positive, implying:
- g<0.
- The circle can touch or intersect the x-axis, which means:
- The equation when y = 0 (i.e., x2+2gx+c=0) must have real roots. Thus, g2−c≥0.
- Additionally, since it does not touch the y-axis, f2−c<0.
- Therefore, the correct match is p: g<0.
4. Statement 4: If the circle touches the positive x-axis and does not intersect the y-axis, then:
- The center of the circle is at (-g, -f) where -g must be positive, implying:
- g<0.
- Since it touches the x-axis, the equation x2+2gx+c=0 must have equal roots, which means:
- g2−c=0 or g2=c.
- Since it does not intersect the y-axis, c>0.
- Therefore, the correct match is s: c>0.
Final Matches:
- Statement 1 → p: g<0
- Statement 2 → r: g2−c<0
- Statement 3 → p: g<0
- Statement 4 → s: c>0
- A circle in the first quadrant has its center at coordinates (-g, -f) where both -g and -f must be positive. This implies:
- g<0 (since -g > 0)
- f<0 (since -f > 0)
- Therefore, the correct match is p: g<0.
- For the circle to lie above the x-axis, the y-coordinate of the center (-f) must be positive, which implies:
- f<0
- The circle can touch or intersect the y-axis, which means:
- The equation when x = 0 (i.e., y2+2fy+c=0) must have real roots. Thus, f2−c≥0.
- Additionally, since it does not touch the x-axis, g2−c<0.
- Therefore, the correct match is r: g2−c<0.
- The center of the circle is at (-g, -f) where -g must be positive, implying:
- g<0.
- The circle can touch or intersect the x-axis, which means:
- The equation when y = 0 (i.e., x2+2gx+c=0) must have real roots. Thus, g2−c≥0.
- Additionally, since it does not touch the y-axis, f2−c<0.
- Therefore, the correct match is p: g<0.
- The center of the circle is at (-g, -f) where -g must be positive, implying:
- g<0.
- Since it touches the x-axis, the equation x2+2gx+c=0 must have equal roots, which means:
- g2−c=0 or g2=c.
- Since it does not intersect the y-axis, c>0.
- Therefore, the correct match is s: c>0.
- Statement 1 → p: g<0
- Statement 2 → r: g2−c<0
- Statement 3 → p: g<0
- Statement 4 → s: c>0
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBook:CENGAGE ENGLISHChapter:COMPLEX NUMBERS AND QUADRATIC EQUATIONSExercise:All Questions
Explore 886 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Book:CENGAGE ENGLISHChapter:DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Exercise:Multiple correct answers type
Explore 11 Videos
Similar Questions
Column I|Column II If the circle lies in the first quadrant, then,|p. g<0 If the circle lies above the x-axis, then|q. g>0 If the circle lies on the left of the y-axis, then|r. g2−c<0 If the circle touches the positive x-axis and does not intersect the y-axis, then|s. c>0
View SolutionArea lying in the first quadrant and bounded by the circle x2+y2=4 and the lines x=0 and x=2 is:
View SolutionLines 5x+12y−10=0 and 5x−12y−40=0 touch a circle C1 of diameter 6. If the center of C1, lies in the first quadrant then the equation of the circle C2, which is concentric with C1, and cuts intercept of length 8 on these lines
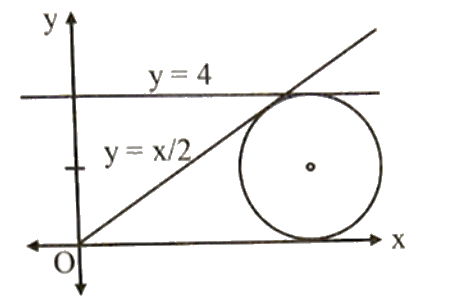
View SolutionThe distance of the y - axis from from the center of the circle which lies in the first quadrant (see figure) and tangent to the lines y=12x,y=4 and the x-axis is
View SolutionIf z = x + iy lies in the third quadrant, then prove that ¯zz also lies in the third quadrant when y<x<0
View SolutionThe equation of the circle of radius 3 that lies in 4th quadrant and touching the lines x=0,y=0 is
View SolutionFind the equation of the circle which lies in the first quadrant and touching each-co ordinate-axis at a distance of 2 units from the origin.
View SolutionIf z lies on the circle I z l = 1, then 2/z lies on
View SolutionArea of the region in the first quadrant exclosed by the X-axis, the line y=x and the circle x2+y2=32 is
View SolutionDraw a circle with centre O and radius 6 cm . Mark points P, Q, R such that P lies on the circle, Q lies in the interior of the circle , and R lies in the exterior of the circle. Rewrite each of the following statements using the correct symbol (=, ⟨or⟩): (i) OQ5 cm (ii) OP.5cm (iii) OR.5 cm
View Solution
