Two circles with radii aandb touch each other externally such that θ is the angle between the direct common tangents, (a>b≥2) . Then prove that θ=2sin−1(a−ba+b) .
To prove that the angle θ between the direct common tangents of two externally touching circles with radii a and b (where a>b≥2) is given by the formula:
θ=2sin−1(a−ba+b)
we can follow these steps:
Step 1: Draw the Circles and Tangents
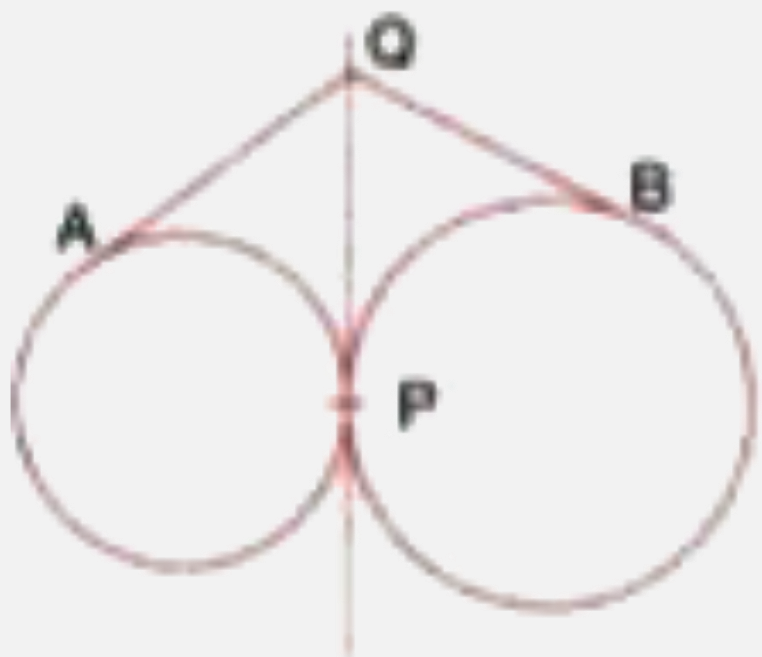
Draw two circles with centers C1 and C2 and radii a and b respectively. Since the circles touch each other externally, the distance between the centers C1 and C2 is a+b.
Step 2: Identify Points and Angles
Let P and Q be the points where the direct common tangents touch the circles. The angle between the tangents at point C (the intersection of the tangents) is θ.
Step 3: Use the Angle Bisector
The line segment C1C2 bisects the angle θ into two equal angles of θ2.
Step 4: Apply the Sine Rule
In triangle C1CP, we can use the definition of sine:
sin(θ2)=oppositehypotenuse=PRAR
where PR is the length from point P to the line connecting the centers C1 and C2 (the perpendicular from P to C1C2), and AR is the distance between the centers C1 and C2, which is a+b.
Step 5: Find Lengths
The length PR can be found using the difference of the radii:
PR=a−b
since P is at a distance b from C2 and a from C1.
Step 6: Substitute into the Sine Formula
Now substituting these lengths into the sine formula gives:
sin(θ2)=a−ba+b
Step 7: Solve for θ
To find θ, we take the inverse sine:
θ2=sin−1(a−ba+b)
Multiplying both sides by 2 gives:
θ=2sin−1(a−ba+b)
Conclusion
Thus, we have proved that:
θ=2sin−1(a−ba+b)
Draw two circles with centers C1 and C2 and radii a and b respectively. Since the circles touch each other externally, the distance between the centers C1 and C2 is a+b.
Let P and Q be the points where the direct common tangents touch the circles. The angle between the tangents at point C (the intersection of the tangents) is θ.
The line segment C1C2 bisects the angle θ into two equal angles of θ2.
In triangle C1CP, we can use the definition of sine:
sin(θ2)=oppositehypotenuse=PRAR
where PR is the length from point P to the line connecting the centers C1 and C2 (the perpendicular from P to C1C2), and AR is the distance between the centers C1 and C2, which is a+b.
The length PR can be found using the difference of the radii:
PR=a−b
since P is at a distance b from C2 and a from C1.
Now substituting these lengths into the sine formula gives:
sin(θ2)=a−ba+b
To find θ, we take the inverse sine:
θ2=sin−1(a−ba+b)
Multiplying both sides by 2 gives:
θ=2sin−1(a−ba+b)
Thus, we have proved that:
θ=2sin−1(a−ba+b)
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - All Questions
886 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
Similar Questions
Knowledge Check
Two circles with radii 25 cm and 9 cm touch each other externally. Find the length of the direct common tangent.
A32 cmB50 cmC40 cmD30 cm
Two circles of radii 4cm and 1cm touch each other externally and θ is the angle contained by their direct common tangents. Then sinθ is equal to (a)2425 (b) 1225 (c)34 (d) none of these
View Solution3 circles of radii a,b,c(a<b<c) touch each other externally and have x-axis as a common tangent then
View SolutionTwo circles touch each other internally. Show that the tangents drawn to the two circles from any point on the common tangent, are equal in length.
View SolutionTwo circle of radii R and r,R>r touch each other externally then the radius of circle which touches both of them externally and also their direct common tangent, is R (b) RrR+r Rr(√R+√r)2 (d) Rr(√R−√r)2
View SolutionTwo circles touch each other externally. The sum of their areas is 58πcm2 and the distance between their centres is 10 cm. Find the radii of the two circles.
View SolutionTwo fixed circles with radii r1andr2,(r1>r2) , respectively, touch each other externally. Then identify the locus of the point of intersection of their direction common tangents.
View SolutionTwo circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
View Solution
