Two circles touch each other internally. Show that the tangents drawn to the two circles from any point on the common tangent, are equal in length.
To solve the problem of showing that the tangents drawn to two internally touching circles from any point on their common tangent are equal in length, we can follow these steps:
1. Understanding the Configuration:
Let the two circles be Circle O (the larger circle) and Circle C (the smaller circle). They touch each other internally at point P.
2. Identify the Point A:
Let A be any point on the common tangent to both circles.
3. Draw Tangents from Point A:
From point A, draw two tangents:
- Tangent AB to Circle O (larger circle)
- Tangent AC to Circle C (smaller circle)
4. Using the Tangent Property:
According to the property of tangents from a point to a circle, the lengths of the tangents drawn from an external point to a circle are equal. Therefore, we can state:
- Length of tangent AB = Length of tangent from A to Circle O = OA
- Length of tangent AC = Length of tangent from A to Circle C = AC
5. Applying the Tangent Length Property:
Since point A is outside both circles, we can say:
- AB = OA (where O is the center of Circle O)
- AC = OC (where C is the center of Circle C)
6. Establishing Equality:
Since both AB and AC are tangents from point A to their respective circles, we can write:
- AB = AC
7. Conclusion:
Therefore, we have shown that the lengths of the tangents drawn from any point on the common tangent to the two circles are equal:
- AB = AC
Final Statement:
Thus, we have proved that the tangents drawn to the two circles from any point on the common tangent are equal in length.
---
Let the two circles be Circle O (the larger circle) and Circle C (the smaller circle). They touch each other internally at point P.
Let A be any point on the common tangent to both circles.
From point A, draw two tangents:
- Tangent AB to Circle O (larger circle)
- Tangent AC to Circle C (smaller circle)
According to the property of tangents from a point to a circle, the lengths of the tangents drawn from an external point to a circle are equal. Therefore, we can state:
- Length of tangent AB = Length of tangent from A to Circle O = OA
- Length of tangent AC = Length of tangent from A to Circle C = AC
Since point A is outside both circles, we can say:
- AB = OA (where O is the center of Circle O)
- AC = OC (where C is the center of Circle C)
Since both AB and AC are tangents from point A to their respective circles, we can write:
- AB = AC
Therefore, we have shown that the lengths of the tangents drawn from any point on the common tangent to the two circles are equal:
- AB = AC
Thus, we have proved that the tangents drawn to the two circles from any point on the common tangent are equal in length.
Topper's Solved these Questions
- TANGENTS AND INTERSECTING CHORDSBook:ICSEChapter:TANGENTS AND INTERSECTING CHORDSExercise:EXERCISE 18 (B)
Explore 18 Videos
- TANGENTS AND INTERSECTING CHORDSBook:ICSEChapter:TANGENTS AND INTERSECTING CHORDSExercise:EXERCISE 18 (C)
Explore 42 Videos
- TANGENTS AND INTERSECTING CHORDSBook:ICSEChapter:TANGENTS AND INTERSECTING CHORDSExercise:EXERCISE 18 (C)
Explore 42 Videos
- SPECIMEN QUESTION PAPER (MATHEMATICS)Book:ICSEChapter:SPECIMEN QUESTION PAPER (MATHEMATICS)Exercise:Section C
Explore 12 Videos
- TRIGONOMETRICAL IDENTITIESBook:ICSEChapter:TRIGONOMETRICAL IDENTITIESExercise:QUESTIONS
Explore 22 Videos
Similar Questions
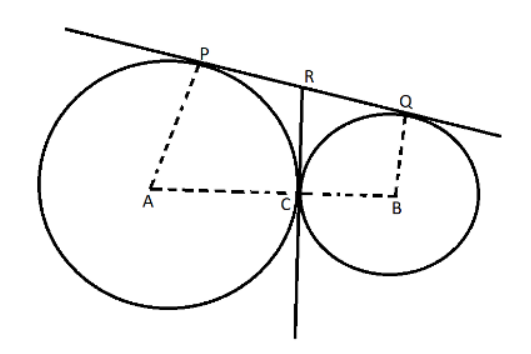
In Figure, two circles touch each other at the point C . Prove that the common tangent to the circles at C , bisects the common tangent at P and Q .
View SolutionIn the figure, two circles touch each other at the point C.Prove that the common tangents to the circles at C, bisect the common tangents at P and Q.
View SolutionProve that the tangent lines drawn from the outer point to the circle are equal? Or
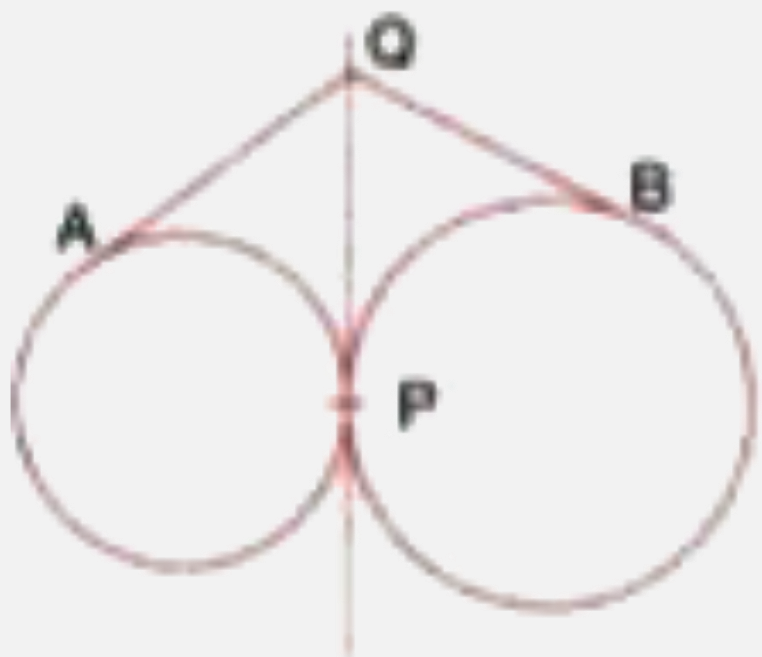
View SolutionTwo circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
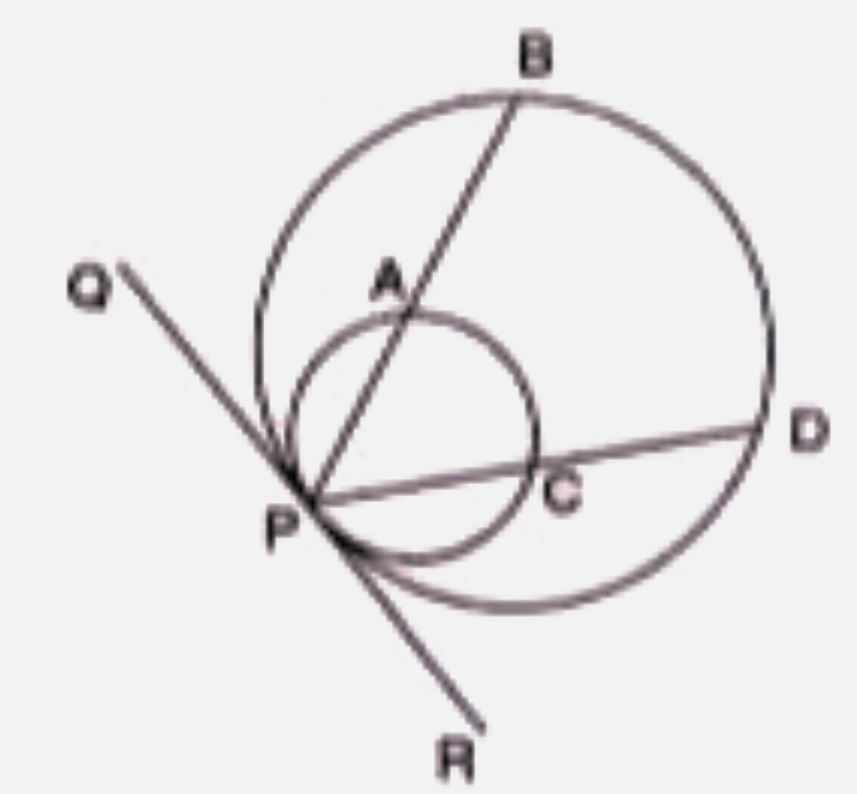
View SolutionTwo circles touch each other internally at point P. QPR is the tangent at P, segments PAB and PCD meet circles at points, A,B,C and D as shown in the figure.
Show that chord AC is parallel to chord BD.
View SolutionIn the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that:
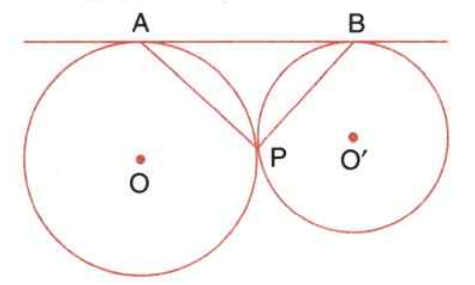
(i) tangent at point P bisects AB
(ii) angle APB=90∘
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View Solution