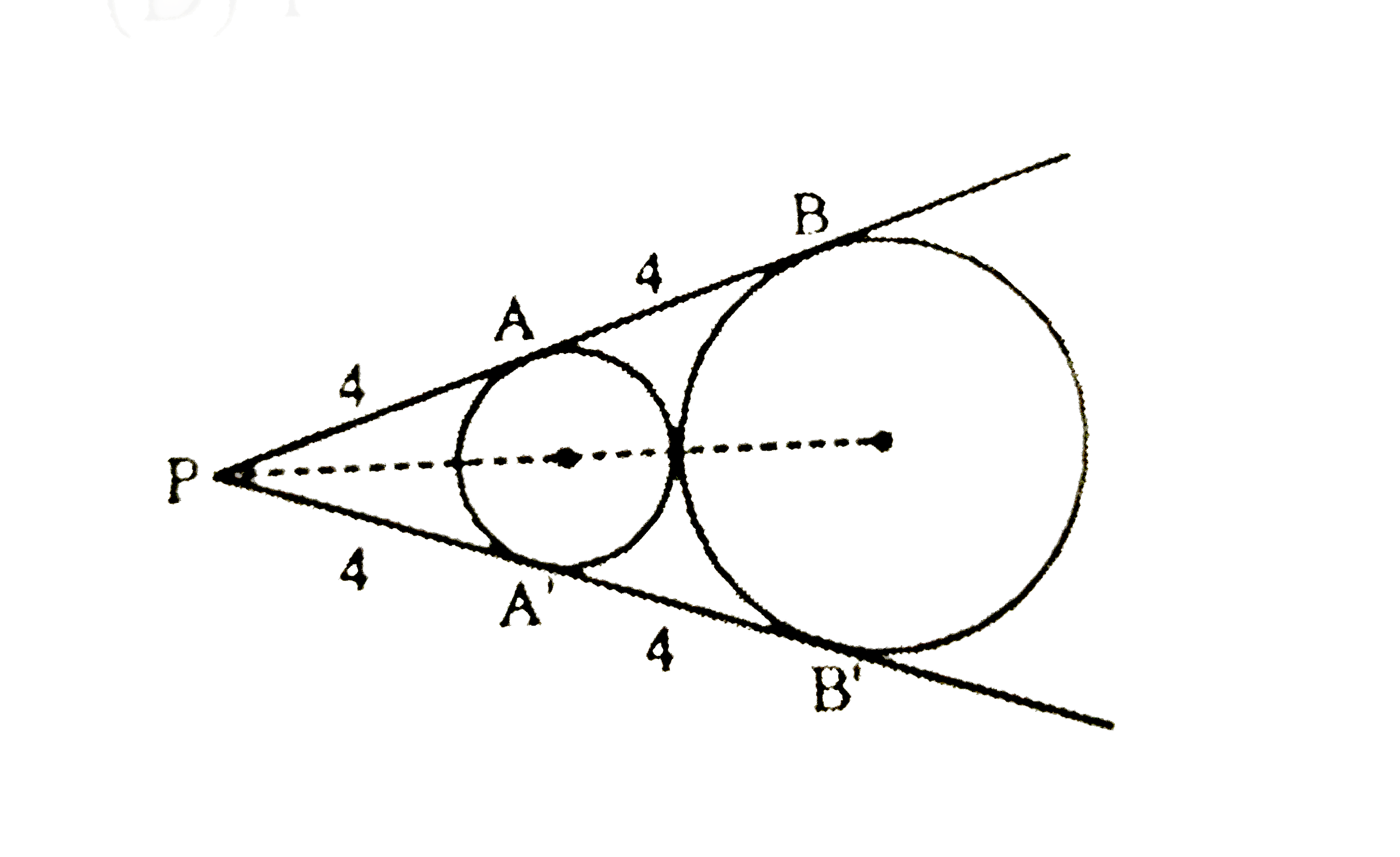
Two circle are externally tangent. Lines PAB and P A 'B ' are common tangents with A and A ' on the smaller circle and B and B ' on the larger circle. If PA=AB=4, then the square of the radius of the circle is___________
To solve the problem, we need to find the square of the radius of the smaller circle given that two circles are externally tangent and that the lengths PA and AB are both equal to 4.
1. Understand the Configuration:
We have two circles that are externally tangent. Let the radius of the smaller circle be R and the radius of the larger circle be 2R. The points P,A,B,A′,B′ represent points on the tangents and the circles.
2. Set Up the Tangent Lengths:
Given that PA=AB=4, we can denote these lengths as follows:
- PA=4
- AB=4
- Therefore, PB=PA+AB=4+4=8.
3. Use the Tangent Segment Theorem:
The lengths from point P to the points of tangency on the circles can be related to the radii of the circles:
- The length from P to the center of the smaller circle C1 is PC1=√PA2+R2=√42+R2=√16+R2.
- The length from P to the center of the larger circle C2 is PC2=√PB2+(2R)2=√82+(2R)2=√64+4R2.
4. Set Up the Relationship Between the Centers:
The distance between the centers of the two circles C1 and C2 can be expressed as:
PC2−PC1=3R
Substituting the expressions we found:
√64+4R2−√16+R2=3R
5. Square Both Sides:
To eliminate the square roots, we square both sides:
(√64+4R2−√16+R2)2=(3R)2
Expanding both sides:
(64+4R2)+(16+R2)−2√(64+4R2)(16+R2)=9R2
This simplifies to:
80+5R2−9R2=2√(64+4R2)(16+R2)
Thus:
80−4R2=2√(64+4R2)(16+R2)
6. Square Again:
Squaring both sides again:
(80−4R2)2=4(64+4R2)(16+R2)
This leads to a polynomial equation in terms of R2.
7. Solve for R2:
After simplifying the equation, we find:
R2=2
8. Conclusion:
The square of the radius of the smaller circle is:
2
We have two circles that are externally tangent. Let the radius of the smaller circle be R and the radius of the larger circle be 2R. The points P,A,B,A′,B′ represent points on the tangents and the circles.
Given that PA=AB=4, we can denote these lengths as follows:
- PA=4
- AB=4
- Therefore, PB=PA+AB=4+4=8.
The lengths from point P to the points of tangency on the circles can be related to the radii of the circles:
- The length from P to the center of the smaller circle C1 is PC1=√PA2+R2=√42+R2=√16+R2.
- The length from P to the center of the larger circle C2 is PC2=√PB2+(2R)2=√82+(2R)2=√64+4R2.
The distance between the centers of the two circles C1 and C2 can be expressed as:
PC2−PC1=3R
Substituting the expressions we found:
√64+4R2−√16+R2=3R
To eliminate the square roots, we square both sides:
(√64+4R2−√16+R2)2=(3R)2
Expanding both sides:
(64+4R2)+(16+R2)−2√(64+4R2)(16+R2)=9R2
This simplifies to:
80+5R2−9R2=2√(64+4R2)(16+R2)
Thus:
80−4R2=2√(64+4R2)(16+R2)
Squaring both sides again:
(80−4R2)2=4(64+4R2)(16+R2)
This leads to a polynomial equation in terms of R2.
After simplifying the equation, we find:
R2=2
The square of the radius of the smaller circle is:
2
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - All Questions
886 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
Similar Questions
Two circles are externally tangent. Lines PAB and PA'B' are common tangents with A and A' on the smaller circle and B' and B' on the larger circle. If PA=AB=4, then area of the smaller circle, is
View SolutionThe line 2x−y+1=0 is tangent to the circle at the point (2, 5) and the centre of the circle lies on x−2y=4. The square of the radius of the circle is
View Solution
Knowledge Check
One circle has a radius of r, and another circle has a radius of 2r. The area of the larger circle is how many times the area of the smaller circle?
A1.5B2C3D4
The figure shows two circles with the same center O. Line segment ¯¯¯¯¯¯AB ios tangent to the smaller circle . If OA=5 and AB=12.what is the ratio of the area of the smaller circle to the area of the larger circle ?A5:13B5:12C25:169D144:169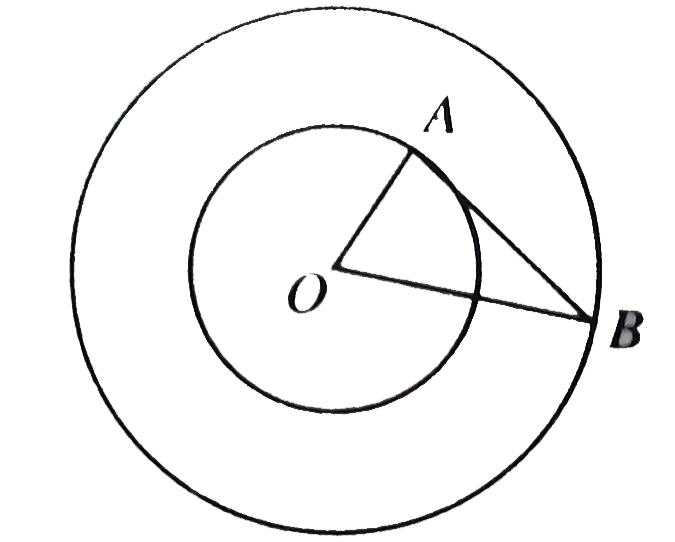
The figure above shows two circles , each with center O. Line segment ¯¯¯¯¯¯AB is tangent to the smaller circle . If OA=5 and AB=12, what is the ratio of the area of the smaller circle to the area of the larger circle ?A5:13B5:12C25:169D25:144
The length of a common internal tangent to two circles is 5 and a common external tangent is 15, then the product of the radii of the two circles is :
View SolutionTwo equal circles touch each other externally at C and AB is a common tangent to the circles. Then, ∠ACB= 60o (b) 45o (c) 30o (d) 90o
View SolutionTwo circles have an external tangent with length 36 cm. The shortest distance between these circles is 14 cm. If the radius of the longer circle is 4 times the radius of the smaller circle then the radius of the larger circle in cms is
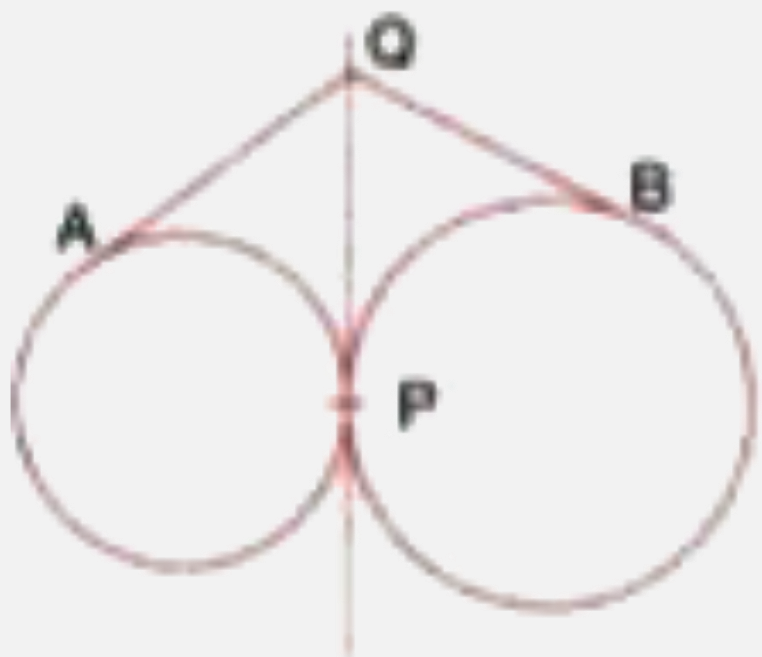
View SolutionTwo circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
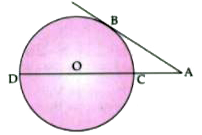
View SolutionIn the given figure O is the centre of the circle and AB is a tangents at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of the circle.
View Solution
