Rectangle ABCD has area 200.An ellipse with area 200π passes through A and C and has foci at B and D. Find the perimeter of the rectangle.
To solve the problem step-by-step, we will follow the reasoning provided in the video transcript and derive the necessary equations to find the perimeter of rectangle ABCD.
Step 1: Understand the given information
- Area of rectangle ABCD = 200 sq. units
- Area of ellipse = 200π sq. units
- The ellipse passes through points A and C and has foci at points B and D.
Step 2: Set up the dimensions of the rectangle
Let the length of side AB (or CD) be L and the length of side AD (or BC) be W. The area of the rectangle can be expressed as:
L×W=200
From this, we can express W in terms of L:
W=200L
Step 3: Determine the diagonal of the rectangle
The diagonal BD of the rectangle can be calculated using the Pythagorean theorem:
BD=√L2+W2=√L2+(200L)2
Step 4: Relate the diagonal to the ellipse parameters
The distance between the foci of the ellipse (points B and D) is given by:
2c=BD
where c is the distance from the center of the ellipse to each focus. The relationship for an ellipse gives us:
c=ae
where a is the semi-major axis and e is the eccentricity. Therefore:
BD=2ae
Step 5: Set up the equation for the ellipse
The area of the ellipse is given by:
Area=πab=200π
From this, we can express:
ab=200
Step 6: Use the property of the ellipse
For points A and C on the ellipse, the sum of the distances from these points to the foci (B and D) is:
BC+CD=2a
Substituting the lengths:
200L+L=2a
Step 7: Solve for a
From the equation ab=200, we can express b in terms of a:
b=200a
Substituting this into the eccentricity formula e=√1−b2a2:
e=
⎷1−(200a)2a2=√1−40000a4
Step 8: Substitute the values into the equations
We can now substitute a and b into the equations derived from the ellipse properties and simplify to find L and W.
Step 9: Calculate the perimeter of the rectangle
The perimeter P of rectangle ABCD is given by:
P=2(L+W)=2(L+200L)
Substituting the values of L that we find from the previous steps will give us the perimeter.
Final Calculation
After substituting and simplifying, we find that:
P=80 units
- Area of rectangle ABCD = 200 sq. units
- Area of ellipse = 200π sq. units
- The ellipse passes through points A and C and has foci at points B and D.
Let the length of side AB (or CD) be L and the length of side AD (or BC) be W. The area of the rectangle can be expressed as:
L×W=200
From this, we can express W in terms of L:
W=200L
The diagonal BD of the rectangle can be calculated using the Pythagorean theorem:
BD=√L2+W2=√L2+(200L)2
The distance between the foci of the ellipse (points B and D) is given by:
2c=BD
where c is the distance from the center of the ellipse to each focus. The relationship for an ellipse gives us:
c=ae
where a is the semi-major axis and e is the eccentricity. Therefore:
BD=2ae
The area of the ellipse is given by:
Area=πab=200π
From this, we can express:
ab=200
For points A and C on the ellipse, the sum of the distances from these points to the foci (B and D) is:
BC+CD=2a
Substituting the lengths:
200L+L=2a
From the equation ab=200, we can express b in terms of a:
b=200a
Substituting this into the eccentricity formula e=√1−b2a2:
e=
⎷1−(200a)2a2=√1−40000a4
We can now substitute a and b into the equations derived from the ellipse properties and simplify to find L and W.
The perimeter P of rectangle ABCD is given by:
P=2(L+W)=2(L+200L)
Substituting the values of L that we find from the previous steps will give us the perimeter.
After substituting and simplifying, we find that:
P=80 units
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - All Questions
886 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
Similar Questions
Knowledge Check
AC, a diagnonal of the rectange ABCD , measure 5 units. The area of the rectangle is 12 sq. units. What is the perimeter of the rectangle?
A7B14C17D20In the figure, ABCD is a rectangle, and F and E are points on AB and BC respectively. The area of ΔDFB is 9 and the area of ΔBED is 24. What is the perimeter of the rectangle?
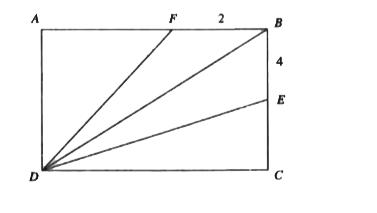 A18B23C30D42
A18B23C30D42
The area of a rectangle is 49cm2 and its breadth is 2.8cm. Find the length of the rectangle.
View SolutionIf a rectangle has breadth 11 m and area 264 sq. m, what is the length of the rectangle? Also, find the perimeter of the rectangle.
View SolutionParallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View SolutionThe area of a square and a rectangle are equal.If the side of the square is 40 cm and the breadth of the rectangle is 25 cm,find the length of the rectangle. Also,find the perimeter of the rectangle.
View SolutionA square and a rectangle have equal area. If side of a square is 24 cm and the length of the rectangle is 32 cm , find
the breadth of the rectangle
View SolutionIn rectangle ABCD, diagonal BD = 26 cm and cotangent of angle ABD = 1.5. Find the area and the perimeter of the rectangle ABCD.
View Solution
