Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
To show that the perimeter of parallelogram ABCD is greater than that of rectangle ABEF, we can follow these steps:
Step 1: Define the Perimeters
The perimeter of a parallelogram is given by the formula:
PABCD=2(AB+AD)
where AB is the length of the base and AD is the height (or the length of the side opposite to base AB).
The perimeter of a rectangle is given by the formula:
PABEF=2(AB+AF)
where AF is the height of the rectangle.
Step 2: Set Up the Equality of Areas
Since the areas of parallelogram ABCD and rectangle ABEF are equal, we have:
AreaABCD=AreaABEF
The area of the parallelogram is given by:
AreaABCD=AB×AD
The area of the rectangle is given by:
AreaABEF=AB×AF
Setting these equal gives:
AB×AD=AB×AF
Step 3: Simplify the Area Equation
Assuming AB≠0, we can divide both sides by AB:
AD=AF
This means that the heights of the parallelogram and rectangle are equal.
Step 4: Analyze the Sides
In parallelogram ABCD, we have:
- AB=CD (opposite sides are equal)
- AD=BC (opposite sides are equal)
In rectangle ABEF, we have:
- AB=EF (opposite sides are equal)
- AF=BE (opposite sides are equal)
Step 5: Compare the Heights
Since AD=AF, we need to compare the lengths AD and AF. In a parallelogram, the side AD is the hypotenuse of triangle ADF (where D is directly above A and F is directly above B). By the properties of triangles, the hypotenuse is always longer than either of the other two sides.
Thus, we can conclude:
AD>AF
Step 6: Conclude the Perimeter Comparison
Now substituting back into the perimeter formulas:
1. For parallelogram ABCD:
PABCD=2(AB+AD)
2. For rectangle ABEF:
PABEF=2(AB+AF)
Since AD>AF, we can say:
PABCD=2(AB+AD)>2(AB+AF)=PABEF
Conclusion
Thus, we have shown that the perimeter of parallelogram ABCD is greater than that of rectangle ABEF:
PABCD>PABEF
---
The perimeter of a parallelogram is given by the formula:
PABCD=2(AB+AD)
where AB is the length of the base and AD is the height (or the length of the side opposite to base AB).
PABEF=2(AB+AF)
where AF is the height of the rectangle.
Since the areas of parallelogram ABCD and rectangle ABEF are equal, we have:
AreaABCD=AreaABEF
The area of the parallelogram is given by:
AreaABCD=AB×AD
The area of the rectangle is given by:
AreaABEF=AB×AF
Setting these equal gives:
AB×AD=AB×AF
Assuming AB≠0, we can divide both sides by AB:
AD=AF
This means that the heights of the parallelogram and rectangle are equal.
In parallelogram ABCD, we have:
- AB=CD (opposite sides are equal)
- AD=BC (opposite sides are equal)
- AB=EF (opposite sides are equal)
- AF=BE (opposite sides are equal)
Since AD=AF, we need to compare the lengths AD and AF. In a parallelogram, the side AD is the hypotenuse of triangle ADF (where D is directly above A and F is directly above B). By the properties of triangles, the hypotenuse is always longer than either of the other two sides.
AD>AF
Now substituting back into the perimeter formulas:
1. For parallelogram ABCD:
PABCD=2(AB+AD)
2. For rectangle ABEF:
PABEF=2(AB+AF)
PABCD=2(AB+AD)>2(AB+AF)=PABEF
Thus, we have shown that the perimeter of parallelogram ABCD is greater than that of rectangle ABEF:
PABCD>PABEF
Similar Questions
Parallelogram ABCD and rectangle ABEF have the same base AB and also have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View SolutionParallelogram ABCD and rectangle ABEF have the same base AB and also have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle. GIVEN : A∣∣gmABCD and a rectangle ABEF with the same base AB and equal areas. TO PROVE : Perimeter of ∣∣gmABCD > Perimeter of rectangle ABEF i.e. AB+BC+CD+AD>AB+BE+EF+AF
View Solution
Knowledge Check
- Question 1 - Select One
In the figure, what is the perimeter of parallelogram ABCD ?
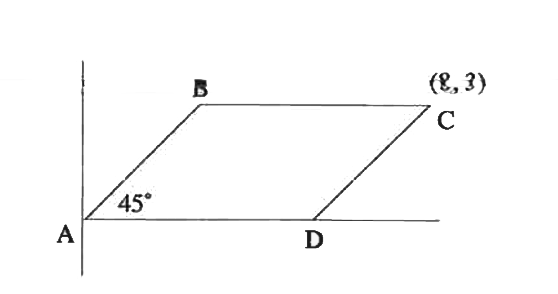 A12B10+6√2C20+√2D24
A12B10+6√2C20+√2D24 - Question 2 - Select One
In the figure, ABCD and ABEF are parallelograms. The area of the quadrilateral ABED is 6. what is the area of the parallelogram ABCD?
 A2B4C4.5D5
A2B4C4.5D5
In figure, if parallelogram ABCD and rectangle ABEM are of equal area, then
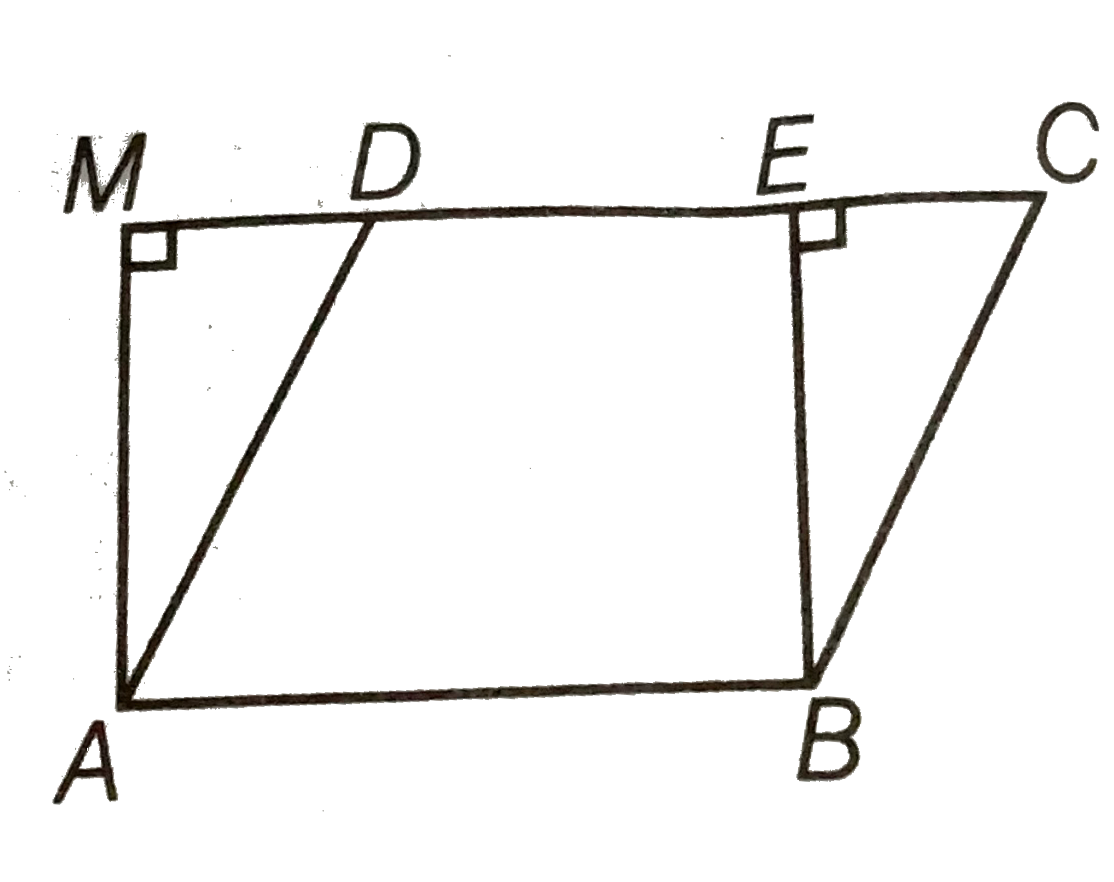 View Solution
View SolutionShow that the bisectors of angles of a parallelogram form a rectangle.
View SolutionShow that the bisectors of angles of a parallelogram form a rectangle.
View SolutionIn the figure, the area of parallelogram ABCD is
 View Solution
View SolutionProve that :
the parallelogram , inscirbed in a circle , is a rectangle.View SolutionIf a triangle and a parallelogram are on the same base and between the same parallels, then prove that the area of the triangle is equal to half the area of the parallelogram.
View Solution

