The perpendicular distance of a corner of uni cube from a diagonal not passing through it is
To solve the problem of finding the perpendicular distance of a corner of a unit cube from a diagonal not passing through it, we can follow these steps:
Step 1: Understanding the Geometry
Consider a unit cube with vertices at points O(0,0,0), A(1,0,0), B(0,1,0), C(0,0,1), and D(1,1,0), E(1,0,1), F(0,1,1), G(1,1,1). We will take the corner C(0,0,1) and the diagonal OP where O(0,0,0) and P(1,1,1).
Step 2: Finding the Direction Vector of the Diagonal
The diagonal OP can be represented by the vector:
→OP=P−O=(1,1,1)−(0,0,0)=(1,1,1)
Step 3: Finding the Magnitude of the Diagonal Vector
The magnitude of the diagonal vector →OP is calculated as:
|→OP|=√12+12+12=√3
Step 4: Finding the Unit Vector in the Direction of the Diagonal
The unit vector in the direction of →OP is given by:
^u=→OP|→OP|=(1,1,1)√3=(1√3,1√3,1√3)
Step 5: Finding the Projection of OC onto OP
The vector OC is given by:
→OC=C−O=(0,0,1)−(0,0,0)=(0,0,1)
Now, we find the projection of →OC onto ^u:
OM=→OC⋅^u=(0,0,1)⋅(1√3,1√3,1√3)=0+0+1√3=1√3
Step 6: Finding the Length of CM
The distance CM can be found using the Pythagorean theorem:
CM2=OC2−OM2
Where OC2=12=1 and OM2=(1√3)2=13:
CM2=1−13=23
Thus,
CM=√23=√63
Final Answer
The perpendicular distance of the corner C from the diagonal OP is:
√63
---
Consider a unit cube with vertices at points O(0,0,0), A(1,0,0), B(0,1,0), C(0,0,1), and D(1,1,0), E(1,0,1), F(0,1,1), G(1,1,1). We will take the corner C(0,0,1) and the diagonal OP where O(0,0,0) and P(1,1,1).
The diagonal OP can be represented by the vector:
→OP=P−O=(1,1,1)−(0,0,0)=(1,1,1)
The magnitude of the diagonal vector →OP is calculated as:
|→OP|=√12+12+12=√3
The unit vector in the direction of →OP is given by:
^u=→OP|→OP|=(1,1,1)√3=(1√3,1√3,1√3)
The vector OC is given by:
→OC=C−O=(0,0,1)−(0,0,0)=(0,0,1)
Now, we find the projection of →OC onto ^u:
OM=→OC⋅^u=(0,0,1)⋅(1√3,1√3,1√3)=0+0+1√3=1√3
The distance CM can be found using the Pythagorean theorem:
CM2=OC2−OM2
Where OC2=12=1 and OM2=(1√3)2=13:
CM2=1−13=23
Thus,
CM=√23=√63
The perpendicular distance of the corner C from the diagonal OP is:
√63
Topper's Solved these Questions
Similar Questions
Find the perpendicular distance of an angular point of a cube from a diagona which does not pass through that angular point. (a) 1√3 (b) 23 (c) √23 (d) √32
View SolutionProve that the perpendicular bisector of a chord of a circle always passes through the centre.
View SolutionProve that the perpendicular bisector of a chord of a circle always passes through the centre.
View SolutionFind the equation of a curve passing through the point (1.1) if the perpendicular distance of the origin from the normal at any point P(x, y) of the curve is equal to the distance of P from the x-axis.
View SolutionThe perpendicular distance from the origin to the plane through the point (2,3,-1) and perpendicular to the vector 3ˆi−4ˆj+7ˆk is
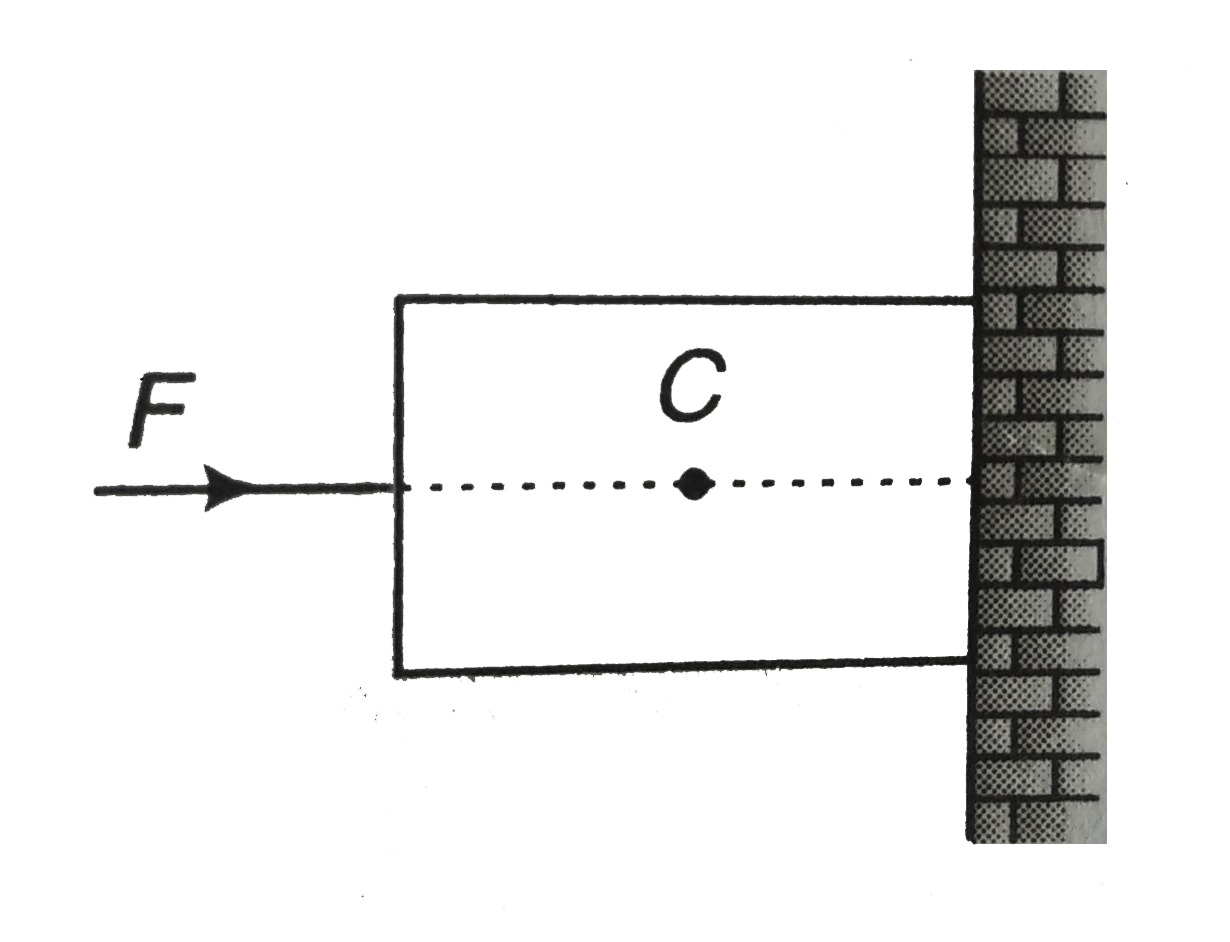
View SolutionA cube of mass 2kg is help stationary against a rough wall by a force F=40N passing through center C . Find perpendicular distance of normal reaction between wall and cube from point C. Side of the cube is 20cmTakeg=10m/s2.
View SolutionA field in the form of a parallelogram has one of its diagonals 42 m long the perpendicular distance of this diagonal from either of the outlying vertices is 10.8 m. Find the area of the field.
View SolutionA field in the form of a parallelogram has one of its diagonals 42 m long the perpendicular distance of this diagonal from either of the outlying vertices is 10.8 m. Find the area of the field.
View SolutionThe length of each side of a cubical closed surface is L metre. If charge 48C is situated at one of the corners of the cube, Find the flux passing through the cube. (In Volt-metre)
View SolutionProve that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
View Solution
