The length of each side of a cubical closed surface is L metre. If charge 48C is situated at one of the corners of the cube, Find the flux passing through the cube. (In Volt-metre)
6∈0
3∈0
48∈0
8∈0
The correct Answer is:A
To find the electric flux passing through a cubical closed surface with a charge located at one of its corners, we can use Gauss's law. Gauss's law states that the electric flux (Φ) through a closed surface is equal to the charge (Q) enclosed by that surface divided by the permittivity of free space (ε₀).
1. Identify the Charge and the Surface:
- We have a charge Q=48C located at one corner of a cube with side length L.
2. Determine the Enclosed Charge:
- Since the charge is located at one corner of the cube, we need to determine how much of this charge is enclosed by the cube. A cube has 8 corners, and the charge at one corner is shared among 8 adjacent cubes.
- Therefore, the charge enclosed by the cube is:
Qenclosed=Q8=48C8=6C
3. Apply Gauss's Law:
- According to Gauss's law, the electric flux through the surface is given by:
Φ=Qenclosedε0
- Here, ε0 (the permittivity of free space) is approximately 8.85×10−12C2/(N⋅m2).
4. Calculate the Electric Flux:
- Substituting the values into the equation:
Φ=6C8.85×10−12C2/(N⋅m2)
- Performing the calculation:
Φ≈68.85×10−12≈6.78×1011N⋅m2/C
5. Final Result:
- The electric flux passing through the cube is approximately 6.78×1011N⋅m2/C or 6.78×1011V⋅m (since 1N⋅m2/C=1V⋅m).
Summary:
The electric flux through the cube is approximately 6.78×1011V⋅m.
- We have a charge Q=48C located at one corner of a cube with side length L.
- Since the charge is located at one corner of the cube, we need to determine how much of this charge is enclosed by the cube. A cube has 8 corners, and the charge at one corner is shared among 8 adjacent cubes.
- Therefore, the charge enclosed by the cube is:
Qenclosed=Q8=48C8=6C
- According to Gauss's law, the electric flux through the surface is given by:
Φ=Qenclosedε0
- Here, ε0 (the permittivity of free space) is approximately 8.85×10−12C2/(N⋅m2).
- Substituting the values into the equation:
Φ=6C8.85×10−12C2/(N⋅m2)
- Performing the calculation:
Φ≈68.85×10−12≈6.78×1011N⋅m2/C
- The electric flux passing through the cube is approximately 6.78×1011N⋅m2/C or 6.78×1011V⋅m (since 1N⋅m2/C=1V⋅m).
The electric flux through the cube is approximately 6.78×1011V⋅m.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise-II
56 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
42 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
Similar Questions
The length of each side of a cubical closed surface is l If charge q is situated on one of the vertices of the cube , then find the electric flux passing through shaded face of the cube.
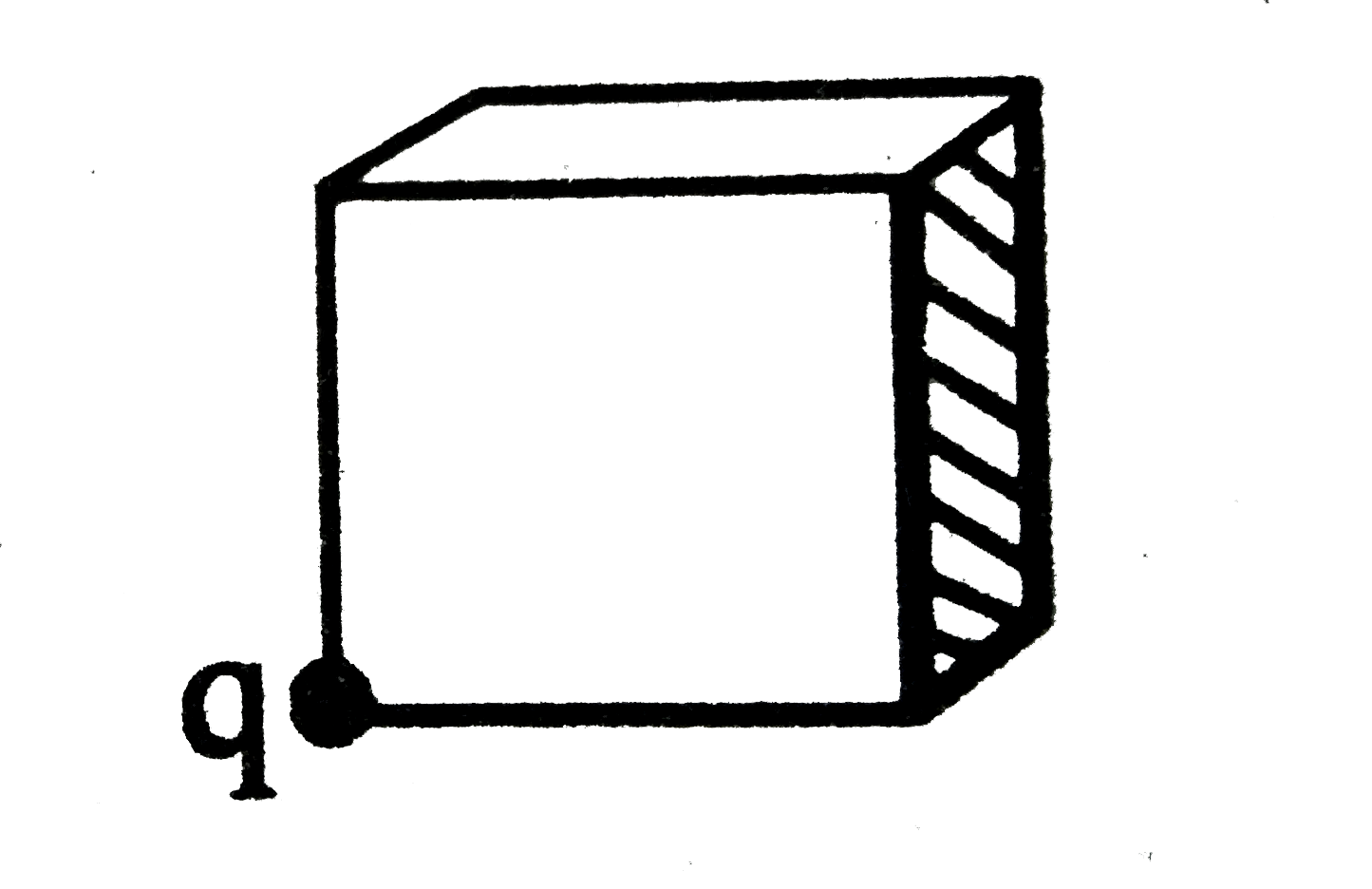 .
.
View SolutionA charge q is placed at the centre of a cube. What is the electric flux passing through the cube?
View SolutionA charge Q is situated at the corner of a cube, the electric flux passing through all the six faces of the cube is :
View SolutionA charge q is placed at point D of the cube. Find the electric flux passing through the EFGH and face AEHD.

View SolutionCharge of 2 C is placed at the centre of a cube. What is the electric flux passing through one face ?
View SolutionIf a point charge q is placed at one corner of a cube, what is the flux linked with the cube?
View SolutionA point charge Q is placed at the corner of a square of side a. Find the flux through the square.
View SolutionA charge Q is situated at the centre of a cube. The electric flux through one of the faces of the cube is
View SolutionA charge Q is placed at each corner of a cube of side a. The potential at the centre of the cube is
View SolutionA charge Q is placed at the centre of a cube. Find the flux of the electric field through the six surfaced of the cube.
View Solution
