The correct Answer is:a→qs;b→p;c→s;d→r
The given lines is x=4y+5,z=3y−6
or x−54=y,z+63=y
or x−54=y1=z+63=λ (say)
Any point on the line is of the form (4λ+5,λ,3λ−6).
The distance between (4λ+5,λ,3λ−6)and(5,3,−6) is 3 units (given). Therefore
(4λ+5−5)2+(λ−3)2+(3λ−6+6)2=9
or 16λ2+λ2+9−6λ+9λ2=9
or 26λ2−6λ=0
or λ=0,3/13
The point is (5,0,−6).
b. The equation of the plane containing the lines x−23=y+35=z+57 and parallel to ˆi+4ˆj+7ˆk is
∣∣
∣
∣∣x−2y+3z+5147357∣∣
∣
∣∣=0
or x−2y+z−3=0
Point (−1,−2,0) lies on this plane.
c. The line passing through points A(2,−3,−1)andB(8,−1,2) is x−28−2=y+3−1+3=z+12+1
or x−26=y+32=z+13=λ (say).
Any point on this line is of the form P(6λ+2,2λ−3,3λ−1), whose distance from point
A(2,−3,−1) is 14 units. Therefore,
PA=14
or PA2=(14)2
⇒ (6λ)2+(2λ)2+(3λ)2=196
or 49λ2=196
or λ2=4
or λ=±2
Therefore, the required points are (14, 1, 5) and (−10,−7,−7). The point nearer to the origin is (14,1,5).
d. Any point on line AB,x2=y−23=z−34=λ is M(2λ,3λ+2,4λ+3). Therefore, the direction ratios of PM are 2λ−3,3λ+3and4λ−8.

But PM⊥AB
∴ 2(2λ−3)+3(3λ+3)+4(4λ−8)=0
4λ−6+9λ+9+16λ−32=0
29λ−29=0
λ=1
Therefore, foot of the perpendicular is M(2,5,7).
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - INTEGER TYPE
10 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - ARCHIVES SUBJECTIVE TYPE
5 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - LINKED COMPREHENSION TYPE
12 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
294 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)
1 Videos
Similar Questions
Find the number of sphere of radius r touching the coordinate axes.
View SolutionFind the equation of the plane passing through the points (2,1,0),(5,0,1) and (4,1,1).
View SolutionGiven four points A(2,1,0),B(1,0,1),C(3,0,1)andD(0,0,2). Point D lies on a line L orthogonal to the plane determined by the points A, B and C.
The equation of the plane ABC is
View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2−0.
View SolutionMatch the statements/expressions in List I with statements/expressions in List II.

View SolutionHow many lines of symmetry does the above figure have ?
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of the figure given below.
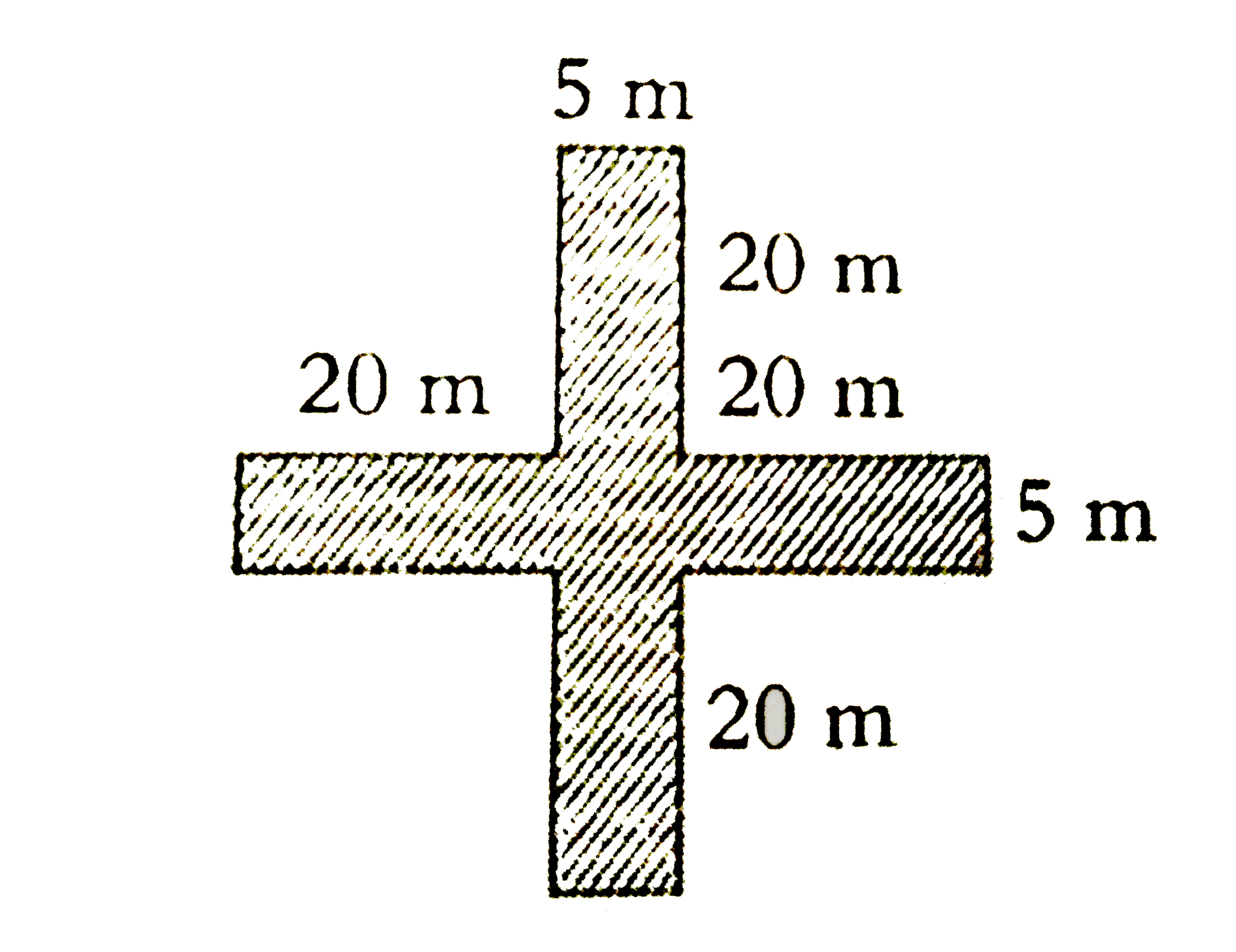
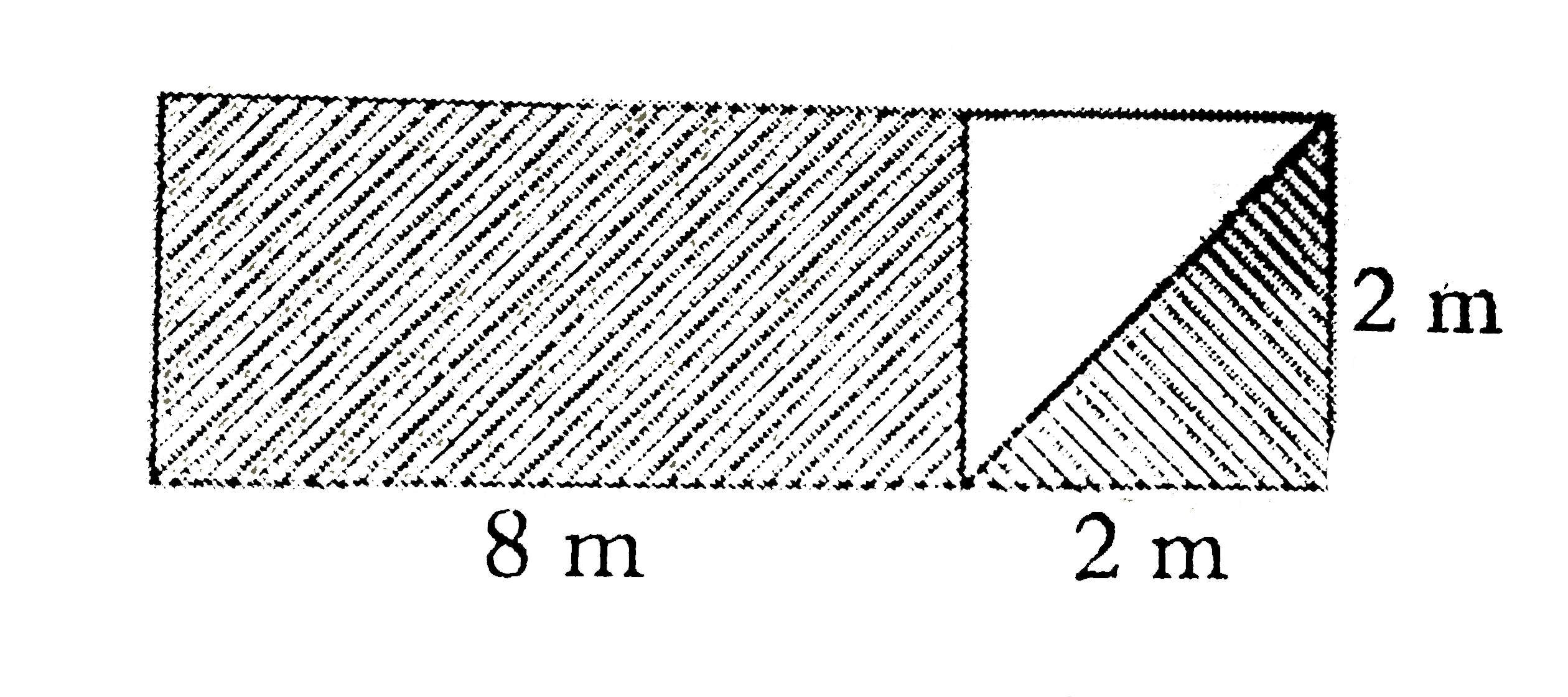
View SolutionThe area of the shaded part in the figure given below is ______.
View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View Solution

