Match the following Column I to Column II
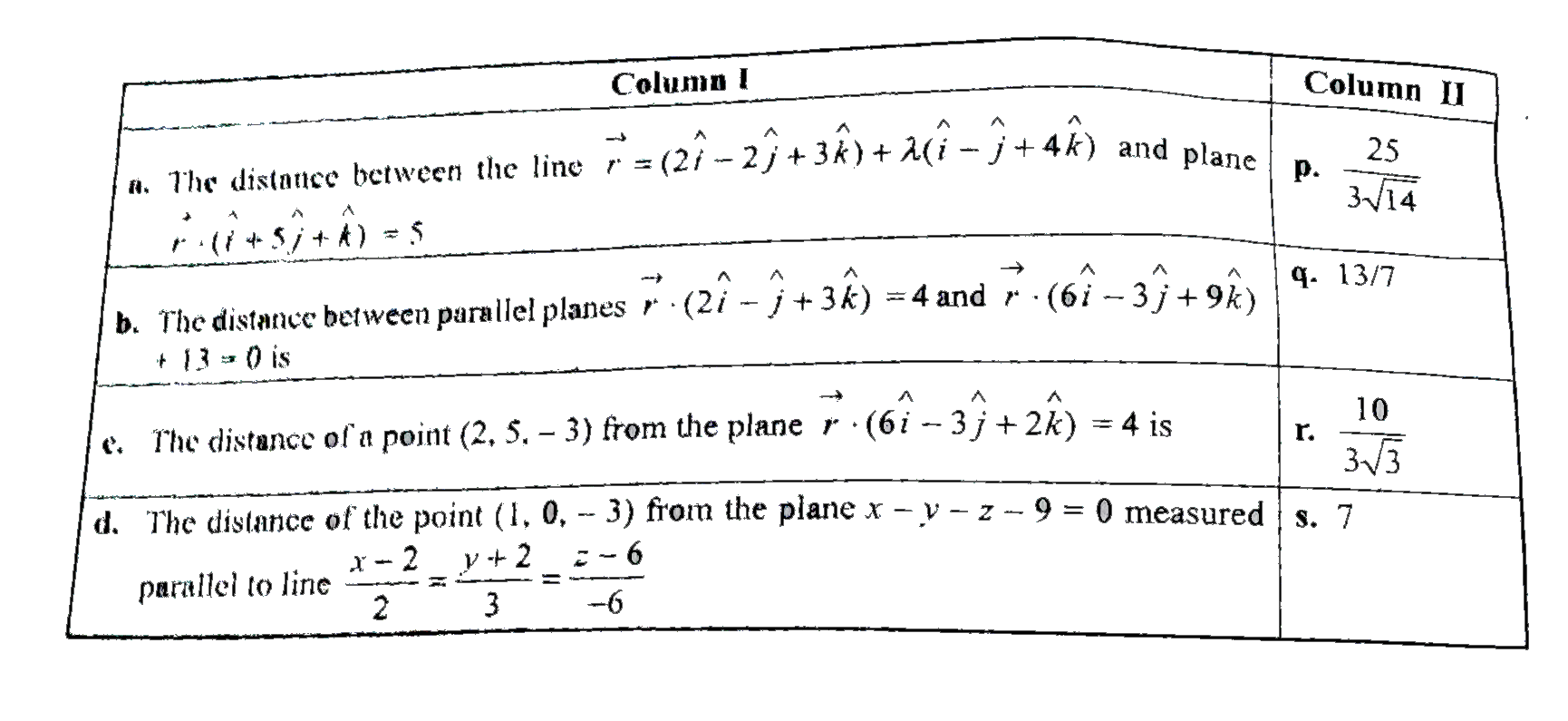
The correct Answer is:a→r;b→p;c→q;d→s
The given line and plane are →r=(2ˆi−2ˆj+3ˆk)+λ(ˆi−ˆj+4ˆk)and→r⋅(ˆi+5ˆj+ˆk)=5, respectively. Since (ˆi−ˆj+4ˆk)⋅(ˆi+5ˆj+ˆk)=0, line and plane are parallel.
Hence, the required distance is equal to distance of point (2,−2,3) from the plane x+5y+z−5=0, which is |2−10+3−5|√1+25+1=103√3
b. The distance between two parallel planes →r⋅(2i−j+3k)=4and→r⋅(6i−3j+9k)+13=0 is
d=|4−(−13/3)|√(2)2+(−1)2+(3)2=(25/3)√14
=253√14
c. The perpendicular distance of the point (2,5,−3) fromt the plane →r⋅(6i−3j+2k)=4or6x−3y+2z−4=0 is
d=|12−15−6−4|√36+9+4
=13/√49=13/7
d. The equation of the line AB is
x−22=y+23=z−6−6
The equation of line passing through (1,0,−3) and parallel to AB is
x−12=y3=z+3−6=r (say)
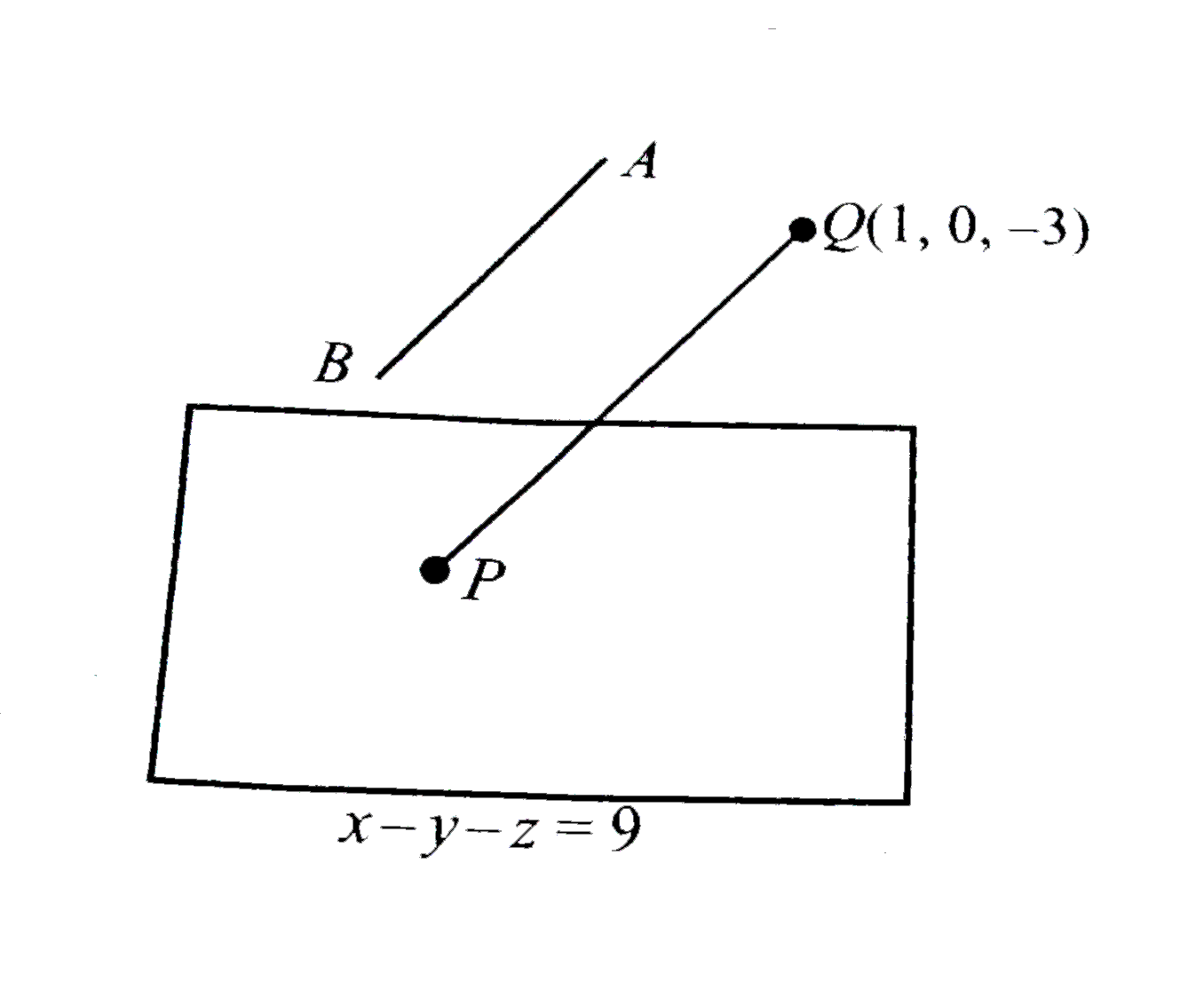
The coordinates of any point on line P(2r+1,3r,−6r−3) which lie on plane
(2r+1)−(3r)−(−6r−3)=9
r=1
Point P≡(3,3,−9)
Required distance
PQ=√(3−1)2+(3−0)2+(−9+3)2
=√4=9+36=7
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - INTEGER TYPE
10 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - ARCHIVES SUBJECTIVE TYPE
5 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - LINKED COMPREHENSION TYPE
12 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
294 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)
1 Videos
Similar Questions
Match the following Column I with Column II
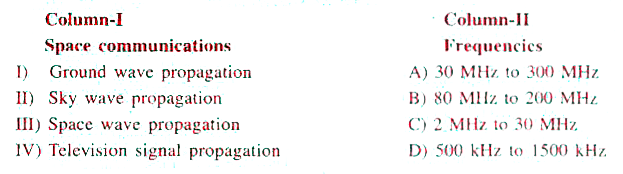
Code
View SolutionMatch the following Column I Column II A. Rhizopus 1. Ascomycetes B. Penicllium 2. Basidiomycetes C. Ustilago 3. Deuteromycetes D. Alternaria 4. Phycomycetes
View SolutionMatch the following (Column I with Column II).

View SolutionMatch the following (Column I with Column II)
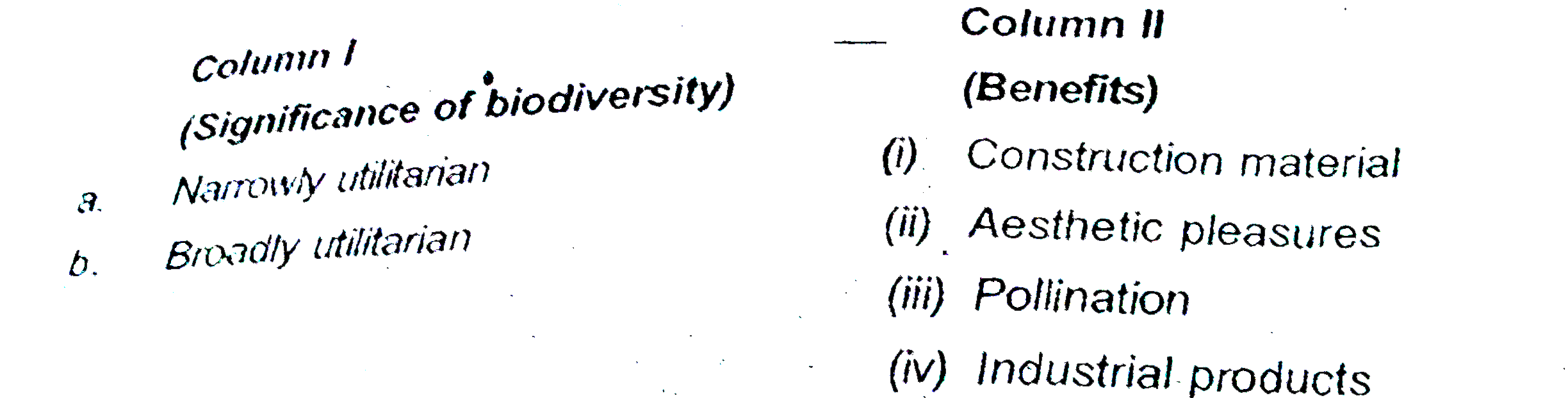
View SolutionMatch the following Column I with column II:

View SolutionMatch the following (Column -I and Column II)
View SolutionMatch the following column I with column II :

View SolutionMatch the following column I with column II and choose the option with the accurate matches.

View SolutionMatch the following column I with column II and choose the correct combination.
ColumnIColumnII(a)Earthworm(i)Gizzard(b)Cockroach(ii)Caecum(c)Frog(iii)Clitellum(d)Rat(iv)Cloaca
View SolutionA block of mass m is thrown upwards with some initial velocity up a rough inclined plane as shown

Match the following Column-I with Column-II

View Solution
