Consider the following sets:
A = set all rectangles in the same plane
B = set all squares in the same plane
C = set all parellegrams in the same plane
Find the following sets : (i)A−B(ii)C−A(iii)A∩C(iv)B∩C(v)B∪C(Vi)A∩B∪C
To solve the problem, we need to analyze the relationships between the sets A, B, and C:
- Set A: All rectangles in the same plane.
- Set B: All squares in the same plane.
- Set C: All parallelograms in the same plane.
Now, let's find the required sets step by step.
(i) A - B
Solution:
A - B represents the set of all rectangles that are not squares. Since every square is a rectangle, A - B will include all rectangles except for those that are squares.
Result:
A - B = Set of all rectangles in the same plane that are not squares.
(ii) C - A
Solution:
C - A represents the set of all parallelograms that are not rectangles. Since rectangles are a specific type of parallelogram, this set will include all parallelograms that do not have right angles.
Result:
C - A = Set of all parallelograms in the same plane that are not rectangles.
(iii) A ∩ C
Solution:
A ∩ C represents the intersection of rectangles and parallelograms. Since all rectangles are also parallelograms, this intersection will be the set of all rectangles.
Result:
A ∩ C = Set of all rectangles in the same plane.
(iv) B ∩ C
Solution:
B ∩ C represents the intersection of squares and parallelograms. Since all squares are also rectangles and thus parallelograms, this intersection will be the set of all squares.
Result:
B ∩ C = Set of all squares in the same plane.
(v) B ∪ C
Solution:
B ∪ C represents the union of squares and parallelograms. Since all squares are parallelograms, this union will simply be the set of all parallelograms.
Result:
B ∪ C = Set of all parallelograms in the same plane.
(vi) A ∩ (B ∪ C)
Solution:
First, we already established that B ∪ C = C. Now, A ∩ C represents the intersection of rectangles and parallelograms. Since all rectangles are parallelograms, this intersection will be the set of all rectangles.
Result:
A ∩ (B ∪ C) = Set of all rectangles in the same plane.
Summary of Results
1. A - B = Set of all rectangles in the same plane that are not squares.
2. C - A = Set of all parallelograms in the same plane that are not rectangles.
3. A ∩ C = Set of all rectangles in the same plane.
4. B ∩ C = Set of all squares in the same plane.
5. B ∪ C = Set of all parallelograms in the same plane.
6. A ∩ (B ∪ C) = Set of all rectangles in the same plane.
- Set B: All squares in the same plane.
- Set C: All parallelograms in the same plane.
Solution:
A - B represents the set of all rectangles that are not squares. Since every square is a rectangle, A - B will include all rectangles except for those that are squares.
A - B = Set of all rectangles in the same plane that are not squares.
Solution:
C - A represents the set of all parallelograms that are not rectangles. Since rectangles are a specific type of parallelogram, this set will include all parallelograms that do not have right angles.
C - A = Set of all parallelograms in the same plane that are not rectangles.
Solution:
A ∩ C represents the intersection of rectangles and parallelograms. Since all rectangles are also parallelograms, this intersection will be the set of all rectangles.
A ∩ C = Set of all rectangles in the same plane.
Solution:
B ∩ C represents the intersection of squares and parallelograms. Since all squares are also rectangles and thus parallelograms, this intersection will be the set of all squares.
B ∩ C = Set of all squares in the same plane.
Solution:
B ∪ C represents the union of squares and parallelograms. Since all squares are parallelograms, this union will simply be the set of all parallelograms.
B ∪ C = Set of all parallelograms in the same plane.
Solution:
First, we already established that B ∪ C = C. Now, A ∩ C represents the intersection of rectangles and parallelograms. Since all rectangles are parallelograms, this intersection will be the set of all rectangles.
A ∩ (B ∪ C) = Set of all rectangles in the same plane.
1. A - B = Set of all rectangles in the same plane that are not squares.
2. C - A = Set of all parallelograms in the same plane that are not rectangles.
3. A ∩ C = Set of all rectangles in the same plane.
4. B ∩ C = Set of all squares in the same plane.
5. B ∪ C = Set of all parallelograms in the same plane.
6. A ∩ (B ∪ C) = Set of all rectangles in the same plane.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Solved Exp11videos
SET THEORY AND REAL NUMBER SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Concept Application Exercise 1.112videos
SET THEORY AND REAL NUMBER SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.311videos
SCALER TRIPLE PRODUCTS
- BOOK - CENGAGE ENGLISHCHAPTER - SOLUTIONS AND PROPERTIES OF TRIANGLE EXERCISE - Comprehension Type6videos
SOLUTIONS AND PROPERTIES OF TRIANGLE
Similar Questions
From the adjoining Venn diagram , find the following sets :
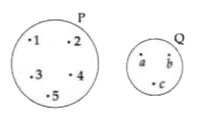
(i) P
(ii) Q
(iii) P∪Q
(iv) P∩QView SolutionFrom the adjoining Venn diagram , find the following sets :
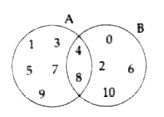
(i) A (ii) B (III) A∪B (iv) A∩BView SolutionFrom the adjoining Venn , diagram , find the following sets :
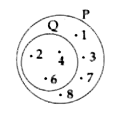
(i) P (ii) Q (iii) P∪Q (iv) P∩QView SolutionConsider the following sets:
A= set ofnaturai numbers which are multiples of 2
B= set ofnaturai numbers which are multiples of 3
C= set ofnaturai numbers which are multiples of 5
Then find the following set
(i)A∪B(ii)B∪C(iii)A−B(iv)B−C(v)A∩C<br>(vi)A∩B∩C(vii)(A∪B)−CView SolutionWrite down all the subsets of the following sets (i) {a} (ii) {a,b} (iii) {1,2,3} (iv) φ
View SolutionIf A={1,2,3,4},B={3,4,5},C={1,5,6}, then findof the following :
(i) A∪B
(ii) A∪(B∩C)
(ii) A−B
(iv) A−(B∪C).View SolutionIf sets A=[−4,1]andB=[0,3), then find the following sets:
(a) A∩B (b) A∪B (c ) A−B
(d) B−A (e ) (A∪B)' (f) (A∩B)'View SolutionFrom the given diagram, find:
(i) (A∪B)−C
(ii) B−(A∩C)
(iii) (B∩C)∪A
Verify: A−(B∩C)=(A−B)∪(A−C)
 View Solution
View SolutionProve A∪(B∩C)=(A∪B)∩(A∪C)
View SolutionUse the given diagram to find:
(i) A∪(B∩C)
(ii) B−(A−C)
(iii) A-B
(iv) A∩B'
is A∩B'=A−B?
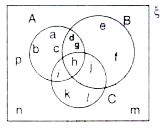 View Solution
View Solution

