If ∣∣x2−2x+2∣∣−∣∣2x2−5x+2∣∣=∣∣x2−3x∣∣ then the set of values of x is
(−∞,0]∪[3,00)
[0,12]∪[2,3]
(−∞,0]∪[12,2]∪[3,∞)
[0,2]∪[3,∞)
The correct Answer is:B
To solve the equation |x2−2x+2|−|2x2−5x+2|=|x2−3x|, we will follow these steps:
Step 1: Rewrite the equation
We start by rewriting the equation:
|x2−2x+2|=|2x2−5x+2|+|x2−3x|
Step 2: Analyze the expressions inside the absolute values
Next, we need to analyze the expressions inside the absolute values. We will find the roots of each quadratic expression to determine the intervals where they change sign.
1. For x2−2x+2:
- The discriminant D=(−2)2−4⋅1⋅2=4−8=−4 (no real roots).
- This expression is always positive since it opens upwards.
2. For 2x2−5x+2:
- The discriminant D=(−5)2−4⋅2⋅2=25−16=9.
- Roots: x=5±34⇒x=2 and x=12.
3. For x2−3x:
- The roots are x(x−3)=0 giving x=0 and x=3.
Step 3: Determine intervals
The critical points are 0,12,2,3. We will analyze the sign of the expressions in the intervals:
- (−∞,0)
- (0,12)
- (12,2)
- (2,3)
- (3,∞)
Step 4: Test each interval
1. Interval (−∞,0):
- |x2−2x+2|=x2−2x+2
- |2x2−5x+2|=−(2x2−5x+2)
- |x2−3x|=−(x2−3x)
2. Interval (0,12):
- |x2−2x+2|=x2−2x+2
- |2x2−5x+2|=−(2x2−5x+2)
- |x2−3x|=−(x2−3x)
3. Interval (12,2):
- |x2−2x+2|=x2−2x+2
- |2x2−5x+2|=2x2−5x+2
- |x2−3x|=−(x2−3x)
4. Interval (2,3):
- |x2−2x+2|=x2−2x+2
- |2x2−5x+2|=2x2−5x+2
- |x2−3x|=x2−3x
5. Interval (3,∞):
- |x2−2x+2|=x2−2x+2
- |2x2−5x+2|=2x2−5x+2
- |x2−3x|=x2−3x
Step 5: Solve inequalities
For each interval, we will set up inequalities based on the signs of the expressions and solve them.
Step 6: Combine solutions
After solving all the inequalities, we will combine the solutions to find the set of values of x.
Final Result
The solution set is:
x∈(0,12)∪(2,3)
We start by rewriting the equation:
|x2−2x+2|=|2x2−5x+2|+|x2−3x|
Next, we need to analyze the expressions inside the absolute values. We will find the roots of each quadratic expression to determine the intervals where they change sign.
- The discriminant D=(−2)2−4⋅1⋅2=4−8=−4 (no real roots).
- This expression is always positive since it opens upwards.
- The discriminant D=(−5)2−4⋅2⋅2=25−16=9.
- Roots: x=5±34⇒x=2 and x=12.
- The roots are x(x−3)=0 giving x=0 and x=3.
The critical points are 0,12,2,3. We will analyze the sign of the expressions in the intervals:
- (−∞,0)
- (0,12)
- (12,2)
- (2,3)
- (3,∞)
1. Interval (−∞,0):
- |x2−2x+2|=x2−2x+2
- |2x2−5x+2|=−(2x2−5x+2)
- |x2−3x|=−(x2−3x)
- |x2−2x+2|=x2−2x+2
- |2x2−5x+2|=−(2x2−5x+2)
- |x2−3x|=−(x2−3x)
- |x2−2x+2|=x2−2x+2
- |2x2−5x+2|=2x2−5x+2
- |x2−3x|=−(x2−3x)
- |x2−2x+2|=x2−2x+2
- |2x2−5x+2|=2x2−5x+2
- |x2−3x|=x2−3x
- |x2−2x+2|=x2−2x+2
- |2x2−5x+2|=2x2−5x+2
- |x2−3x|=x2−3x
For each interval, we will set up inequalities based on the signs of the expressions and solve them.
After solving all the inequalities, we will combine the solutions to find the set of values of x.
The solution set is:
x∈(0,12)∪(2,3)
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Archives1videos
SET THEORY AND REAL NUMBER SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Concept Application Exercise 1.512videos
SET THEORY AND REAL NUMBER SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.311videos
SCALER TRIPLE PRODUCTS
- BOOK - CENGAGE ENGLISHCHAPTER - SOLUTIONS AND PROPERTIES OF TRIANGLE EXERCISE - Comprehension Type6videos
SOLUTIONS AND PROPERTIES OF TRIANGLE
Similar Questions
Knowledge Check
- Question 1 - Select One
A teacher wrote the following polynomial on the board :
2x3−3x2+4x+7,x3−19x−30,2x2+5x+2,3x+2,4x2,2x2−5x+p,2x2+5x+q
Now she asked following questions to the students
If 2 x + 1 is a factors of 2x2−5x+p then the value of p isA3B6C−6D−3 - Question 2 - Select One
If −5<2x−3≤x+2,x∈R, then the solution set of x on the number line is
A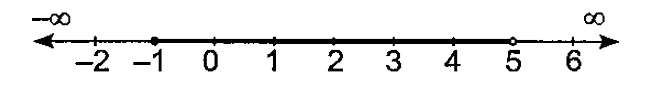 B
B C
C D
D
Let f(x)={3x2−2x+10x<1−2x>1
The set of values of b for which f(x) has greatest value at x=1 isView SolutionLet f(x)=⎧⎪⎨⎪⎩x3−x2+10x−5,x≤1−2x+log2(b2−2),x>1. The set of values of b for which f(x) has greatest value at x= 1 is given by .
View SolutionIf |A| = 2 and A=∣∣∣2x65x1∣∣∣ then find the value of x
View SolutionIf 3x+22x≥5x, then the solution set for x, is
View SolutionLet f(x)={2−∣∣x2+5x+6∣∣x≠−2b2+1x=−2
Has relative maximum at x=−2, then complete set of values b can take is:View SolutionLet A=⎡⎢⎣3x216x⎤⎥⎦,B=[a,b,c]and C=⎡⎢ ⎢⎣(x+2)25x22x5x22x(x+2)22x(x+2)25x2⎤⎥ ⎥⎦ be three given matrices, where a,b,candx∈R. Given that tr(AB)=tr(C). If f(x)=ax2+bx+c, then the value of f(1) is ______.
View Solution

