The graph of is as shown in the following figure.

Find the following values:
(i)
(i) At x = 4, f(x) is continuous and
(ii).
(iii) When x approaches 0 from its right-hand side, the value of f(x) approaches - 1.
Hence .
(iv) When x approaches 0 from its left hand, the value of f(x) approaches - 2.
Hence .
(v) Clearly .
(vi) f(-2) = 8, see the dot at point (-2, 8) in the graph.
(vii) When x approaches 2 from its left - hand side, the value of f(x) approaches 7.
Hence .
(viii) When x approaches - 2 from its left-hand side, the value of f(x) is exactly 6 as . Hence (exact).
(ix) Since y = f(x) is continuous at .
(x) f (0) =- 1.5.
(xi) = value of f(x) to which it is approaching when x is approaching - 2 from its right - hand side. From the graph , this value is 2. Hence .
(xii) = value of f (x) to which it is approaching when x is approaching - 3 from its left-hand side. Since .
Topper's Solved these Questions
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE ENGLISHCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.16
1 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE ENGLISHCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.17
1 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE ENGLISHCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.14
1 Videos
- FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - FUNCTIONSEXERCISE - Comprehension Type
7 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
18 Videos
Similar Questions
The graph of y = f(x) is as shown in the following figure.
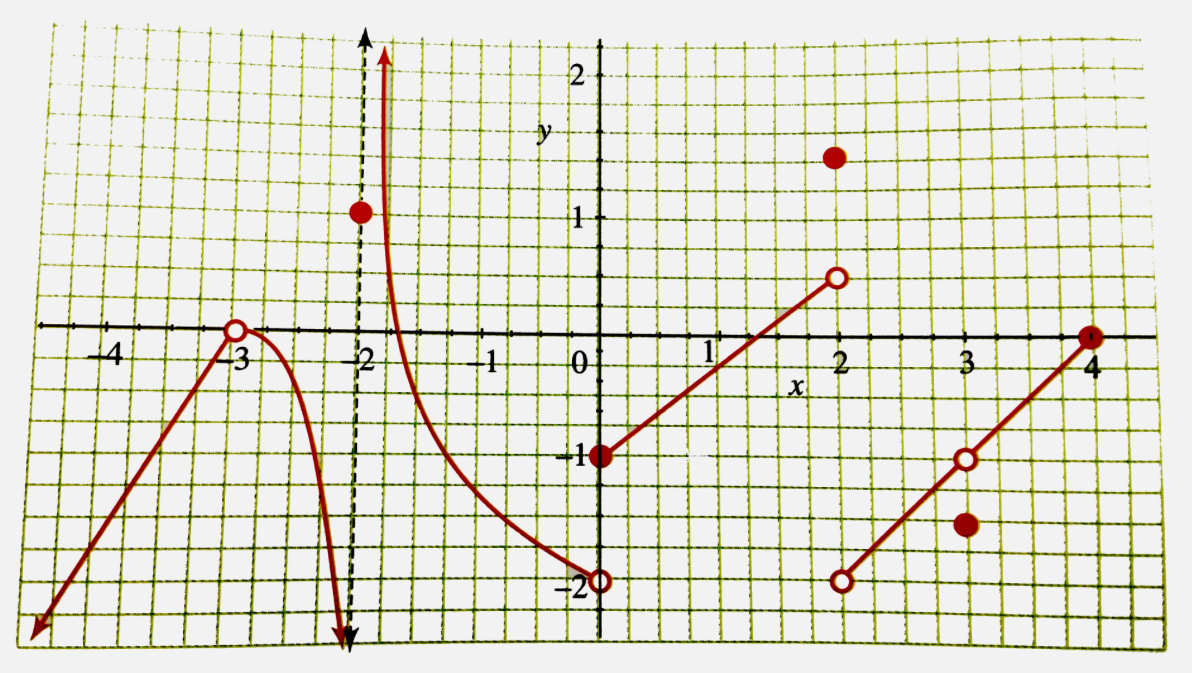
Find the following values
(i)f(−3) (ii)f(−2) (iii)f(0)
(iv)f(2) (v)f(3) (vi)limx→−3f(x)
(vii)limx→0f(x) (viii)limx→2f(x) (ix)limx→3f(x)
(x)limx→2−f(x) (ξ)limx→−2+f(x) (xii)limx→0−f(x)
(x iii) limx→0+f(x)
View SolutionThe graph of y = f(x) is as shown in the following figure.

Find the following values
(i)f(−3) (ii)f(−2) (iii)f(0)
(iv)f(2) (v)f(3) (vi)limx→−3f(x)
(vii)limx→0f(x) (viii)limx→2f(x) (ix)limx→3f(x)
(x)limx→2−f(x) (ξ)limx→−2+f(x) (xii)limx→0−f(x)
(x iii) limx→0+f(x)
View Solutionif f(x)={−1,∀x≤−1,x3∀−1≤x<1,(1−x)∀1<x<2,3−x2∀x>2} then (i)f(x)=1, (ii) limx→−1+f(x)=1 (iii) limx→2+f(x)=−1 (iv)limx→2−f(x)=0
View SolutionIf limx→−2f(x)x2=1, find (i) limx→−2f(x) and (ii) limx→−2f(x)x
View SolutionFind limx→0f(x) and limx→1f(x), where
f(x)={2x+3,x≤03(x+1),x>0
View SolutionIf limx→−2f(x)x2=1, find (i)limx→−2f(x);(ii)limx→−2f(x)x
View SolutionIf f(x) = {x|x| for x≠00 for x=0 , find Limx→0f(x)
View SolutionFind limX→0f(x) where f(x)={xx≠05x=0}
View SolutionFind limX→0f(x) where f(x)={xx≠05x=0}
View SolutionLet f (x) be a function continuous for all except at x =0 such that
f'(x)>0∀x>0andf'(x)<0∀x<0.
If limx→0+f(x)=10,limx→0−f(x)=15andf(0)=12, then limx→0f(x3−x2)limx→0f(2x4−x5)+limx→0[f(x3−x2)]limx→0[f(2x4−x5)]=
[.] denotes greatest integer Function)
View Solution
