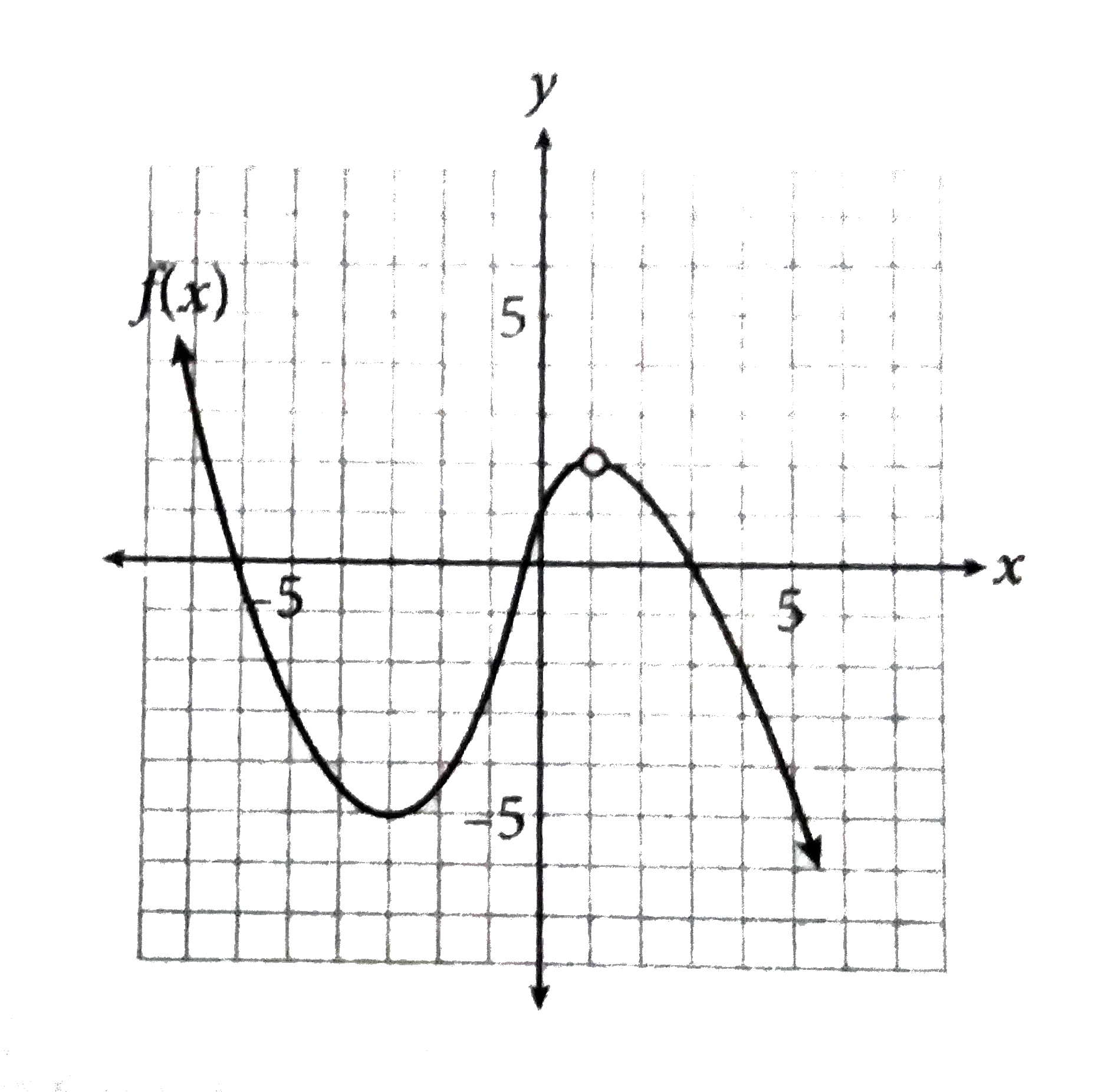
Following is the graph of y = f'(x) and f(0) = 0 .
(a) What type of function y = f'(x) is ? Odd or even?
(b) What type of function y = f(x) is ? Odd or even?
(c) What is the value of ∫a−af(x)dx?
(d) Has y = f(x) point of inflection?
(e) What is the nature of y = f(x)? Monotonic or non-monotonic?
(a) The graph of y = f'(x) is symmetrical about the y-axis, so f(x) is an even function.
(b) f(0) = 0, so f(x) is an odd function [derivative of an odd function is even].
(c) As f(x) is odd, so a∫−af(x)dx=0
(d) f''(x)>0asx<0andf''(x)<0as x>0. Therefore, x = 0 is the point of inflexion.
(e) f'(x)≤0,∀x, so f(x) is always decreasing.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercises 1.171videos
GETTING STARTED WITH GRAPHS
- BOOK - CENGAGE ENGLISHCHAPTER - FUNCTIONSEXERCISE - Comprehension Type7videos
FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises18videos
GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
If f(x) is a linear function and the slope of y=f(x) is 12, what is the slope of y=f−1(x) ?
A−2B−12C12D2
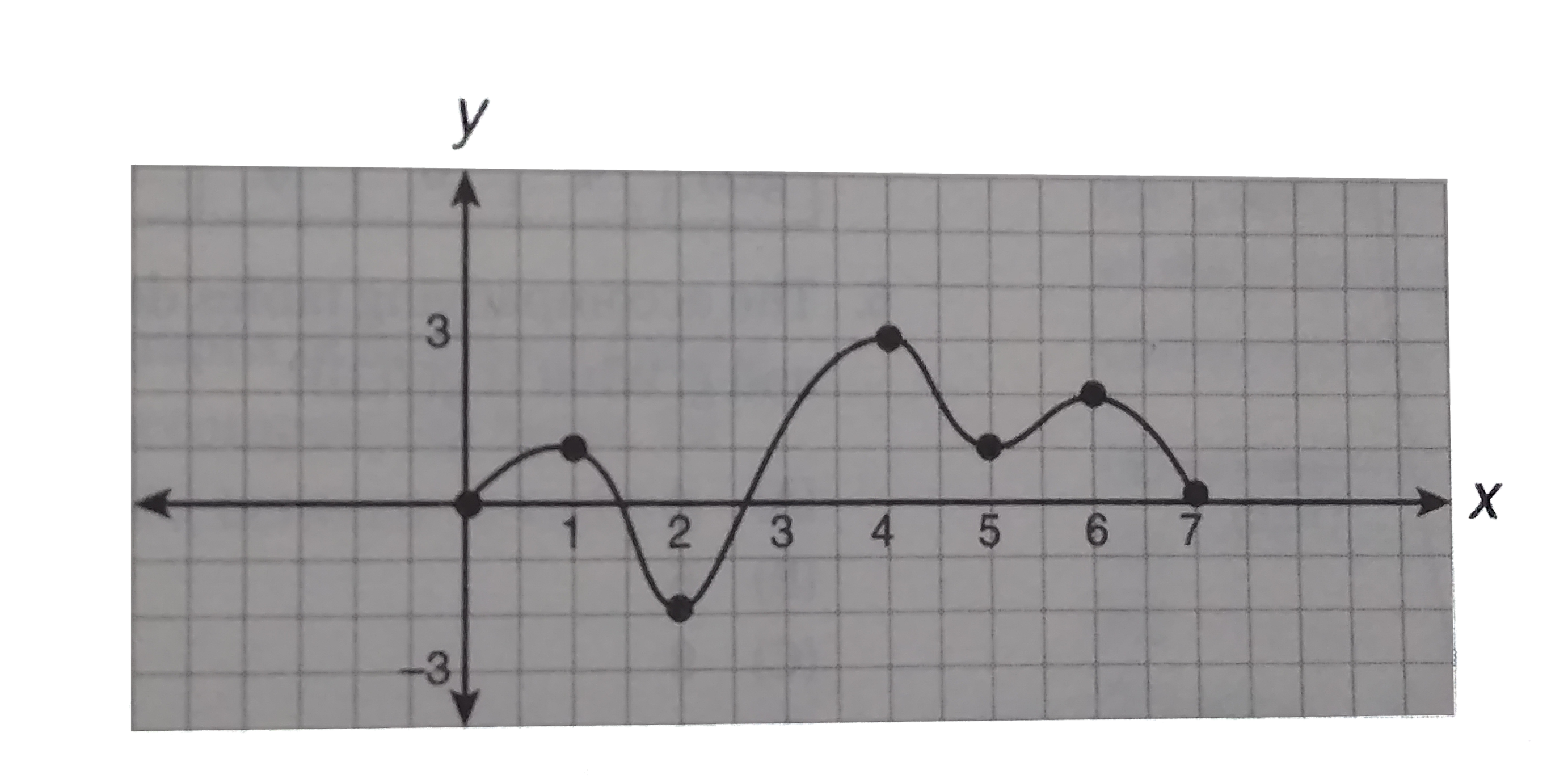
The graph of y=f(x) is given above. For what value of x is y=f(x-4) undefined?View SolutionIf the graph of the function y=f(x) is as shown :

the graph of y=12(|f(x)|−f(x)) isView SolutionThe graph of y=f''(x) for a function f is shown.
Number of points of inflection for y=f(x) is….. .
 View Solution
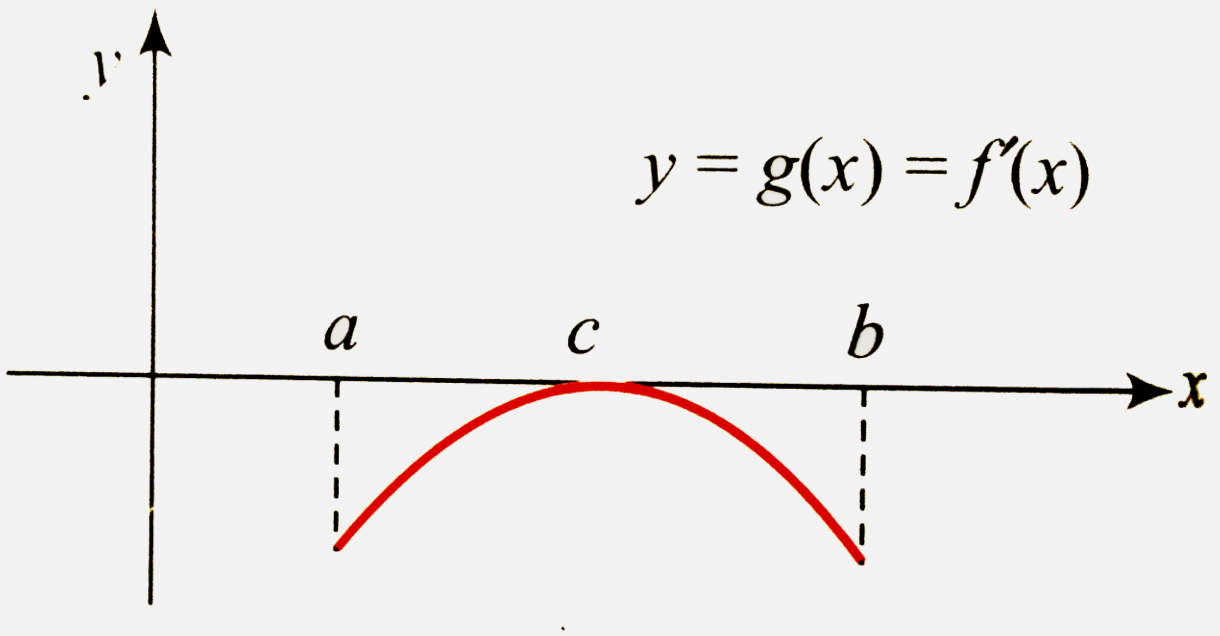
View SolutionFollowing is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, a≤x≤b.
(c) How many points of inflection the graph of y=f(x),a≤x≤b, has?
(d) Find the points of local maxima/minima ofy=f(x),a<xb.
(e) How many roots equation f''(x)=0 has?
 View Solution
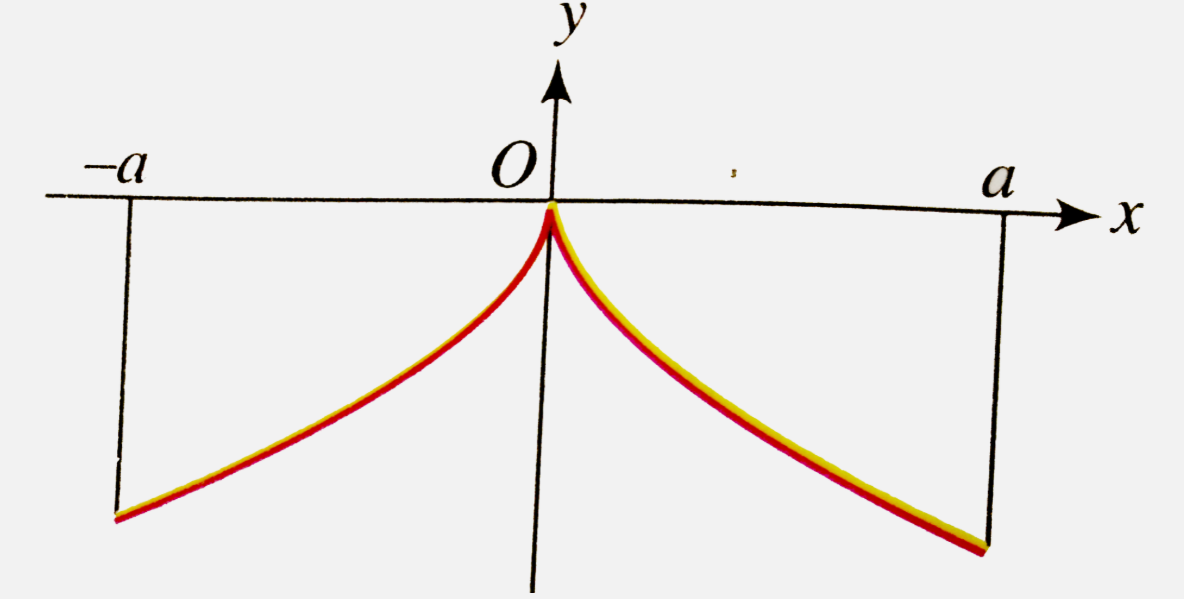
View SolutionIf the graph of the function y=f(x) is as shown :

The graph of y=1/2(|f(x)|−f(x)) isView SolutionIf the graph of the function y=f(x) is as shown :

The graph of y=1/2(|f(x)|−f(x)) isView SolutionIf f(x) is an odd function, then the curve y=f(x) is symmetric
View Solution