Question

Draw the rough sketch of the curve $y={(x-1)}^2{(x-3)}^3$.

Explanation

We have `y=f(x)=(x-1)^(2)(3-x)^(3)=-(x-1)^(2)(x-3)^(3)`
The sign scheme of `y=f(x)` is as follows.

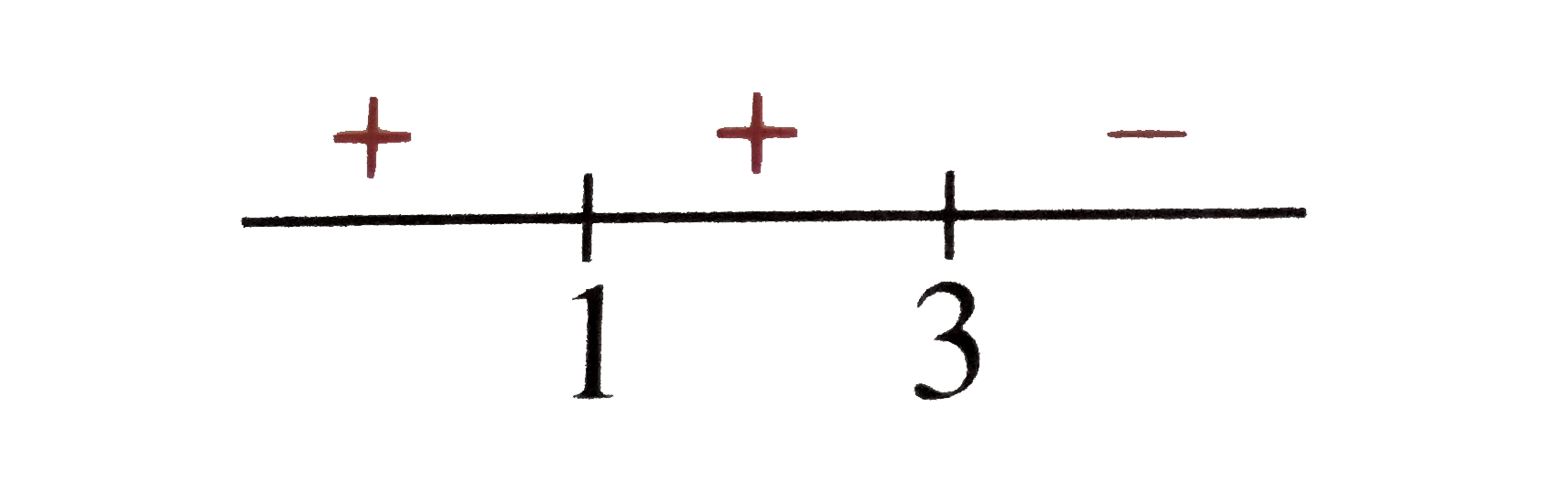
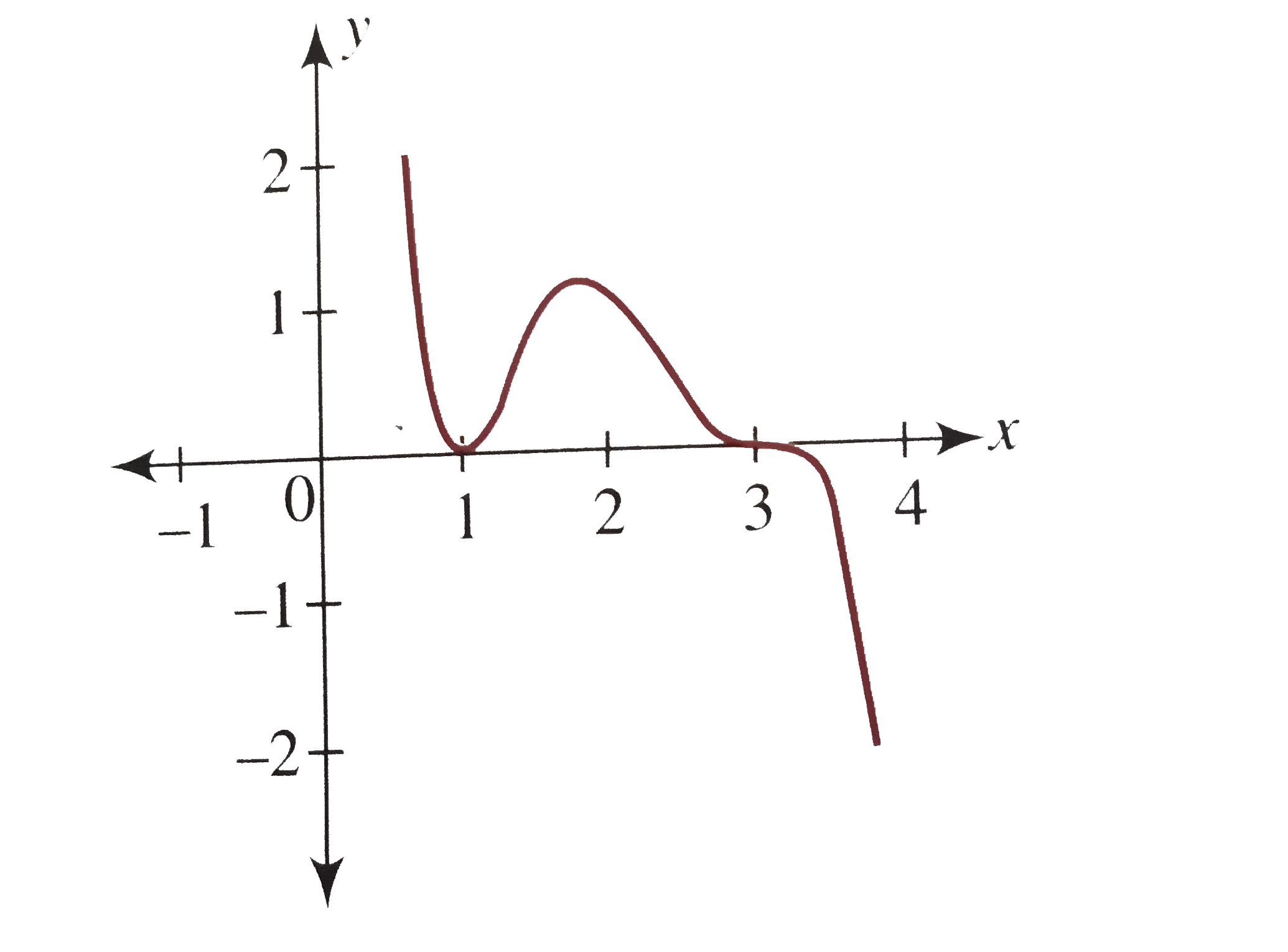
`(x-3)^(3) rarr` Curve crosses the x-axis at (3,0) and also touches the x-axis.
`(x-1)^(2) rarr ` Curve does not cross the x-axis but touches the x-axis at (1,0).
Therefore, the graph of the function is as shown in the following figure.